フーリェ級数
1 広義のフーリェ級数展開
\[関数 \ f(x)\ が、区間 \ [a,\ b]\ 上の正規直交系 \ \ \{\varphi_n(x)\}\ \ によって、f=\sum_{i=0}^{\infty} c_i\varphi_i \ \ とあらわされるとき\] $\hspace{3em} (直交系については($正規直交系$)をご覧ください。)$\begin{eqnarray*} (\varphi_n,f) &=&(\varphi_n, c_0\varphi_0+ c_1\varphi_1+ \cdots c_n\varphi_n+\cdots )\\ \\ &=&(\varphi_n, c_0\varphi_0) + (\varphi_n,c_1\varphi_1)+ \cdots + (\varphi_n, c_n\varphi_n)+\cdots \\ \\ &=&c_n(\varphi_n ,\varphi_n)\\ \\ &=&c_n \end{eqnarray*} $\quad したがって$
\[\qquad c_n=(\varphi_n,f)=\int _a^b f(x)\varphi_n(x)dx \] $\quad より、係数 \ c_n \ が求められるが \ f(x)\ のこのような表現を(広義の)フーリェ級数展開といいます。$
$\quad なお、フーリェ係数 \ c_n\ は、\alpha_n\ がいろいろな値をとったとき、$
\[||f-\sum_i \alpha_i\varphi_i||^2=\int_a^b \big\{f(x)-\sum_i \alpha_i\varphi_i(x)\big\}^2dx を最小にする値です。\] $\hspace{3em} (このことについては($最小二乗近似$)をご覧ください。)$
2 フーリェ級数の項数による近似の差
$\quad \varepsilon_m=f-f_m \ \ とおくと$
\begin{eqnarray*} ||\varepsilon_{m+1}||^2 &=&||f-f_{m+1}||^2 \\ \\ &=&||f-f_m - c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||f-f_m||^2-2(f-f_m,c_{m+1}\varphi_{m+1})+ ||c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||f-f_m||^2-2(c_{m+1}\varphi_{m+1}+c_{m+2}\varphi_{m+2}+\cdots ,\ c_{m+1}\varphi_{m+1})+ ||c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||f-f_m||^2-2(c_{m+1}\varphi_{m+1},\ c_{m+1}\varphi_{m+1})+ ||c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||f-f_m||^2-2||c_{m+1}\varphi_{m+1}||^2 + ||c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||f-f_m||^2-||c_{m+1}\varphi_{m+1}||^2 \\ \\ &=&||\varepsilon_m ||^2-||c_{m+1}||^2 \\ \end{eqnarray*}
$\quad ||\varepsilon_m ||^2 - ||\varepsilon_{m+1}||^2=||c_{m+1}||^2 \geqq 0 \quad だから \quad ||\varepsilon_m || \geqq ||\varepsilon_{m+1}|| $
$\quad つまり、フーリェ級数で項を多くとればとるほど、和は \ f(x)\ に近づくということです。$
3 狭義のフーリェ級数展開
$\quad 区間 \ [-\pi,\ \pi]\ において \ \ \{1,\ \cos nx,\ \sin nx\}\ \ (n=1,\ 2,\ \cdots )\ \ は直交系をなし、\{\cfrac{1}{\sqrt{2\pi}},\cfrac{1}{\sqrt{\pi}}\cos nx,\cfrac{1}{\sqrt{\pi}}\sin nx\}\ \ は$
$\quad 正規直交系となります。\quad (このことについては($正規直交系$)をご覧ください。)$
$\quad ここでは、f(x)\ は \ 2\pi\ を周期とする、区分的になめらか(ある区間で有限個の点を除いて \ C^1\ 級のこと)な$
$\quad 周期関数とします。$
\[c_0=(\varphi_0,f)=(\cfrac{1}{\sqrt{2\pi}},\ f)=\int _{-\pi}^{\pi} \cfrac{1}{\sqrt{2\pi}}f(x)dx =\cfrac{1}{\sqrt{2\pi}}\int _{-\pi}^{\pi}f(x)dx \] \[c_{2n-1}=(\varphi_{2n-1},f)=(\cfrac{\cos nx}{\sqrt{\pi}},\ f)=\int _{-\pi}^{\pi} \cfrac{\cos nx}{\sqrt{\pi}}f(x)dx =\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\cos nx dx \] \[c_{2n}=(\varphi_{2n},f)=(\cfrac{\sin nx}{\sqrt{\pi}},\ f)=\int _{-\pi}^{\pi} \cfrac{\sin nx}{\sqrt{\pi}}f(x)dx =\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\sin nx dx \] $よって$
\begin{eqnarray*} f(x) &=&\sum_{n=0}^{\infty} c_n\varphi_n \\ \\ &=&c_0\varphi_0+\sum_{n=1}^{\infty} c_n\varphi_n \\ \\ &=&c_0\varphi_0 + \sum_{n=1}^{\infty} (c_{2n-1}\varphi_{2n-1}+c_{2n}\varphi_{2n}) \\ \\ &=&\big(\cfrac{1}{\sqrt{2\pi}}\int _{-\pi}^{\pi}f(x)dx \big) \times \cfrac{1}{\sqrt{2\pi}} + \sum_{n=1}^{\infty} \Big\{ \big(\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\cos nx dx \big) \times \cfrac{\cos nx}{\sqrt{\pi}}+ \big(\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\sin nx dx \big) \times \cfrac{\sin nx}{\sqrt{\pi}}\Big\}\\ \\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}f(x)dx + \sum_{n=1}^{\infty} \Big\{\big (\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(x)\cos nx dx\big)\cos nx + \big(\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(x)\sin nx dx \big)\sin nx \Big\}\\ \end{eqnarray*}
\[a_0=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx ,\qquad a_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx , \qquad b_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx を(狭義の)フーリェ係数といい、\] \[f(x)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nx+b_n\sin nx) \ \ を \ f(x)\ の(狭義の)フーリェ級数展開といいます。\]
$\qquad (ほとんどの解説書は、これを定義として始めます。)$
、
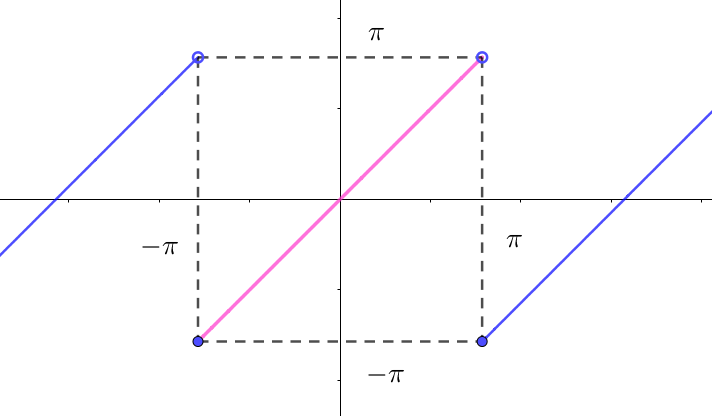
$例1 \quad 右図のグラフのような「ノコギリ波」のフーリェ級数展開を$
$\qquad 求めてみましょう。$
$\quad f(x)\ は周期 \ 2\pi \ の周期関数で$
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
x \quad (-\pi < x < \pi)\\
0 \quad (x=-\pi,\pi)\\
\end{array} \right.
\]
$\quad f(x)\ は奇関数だから \quad a_0=0,\quad a_n=0$
\begin{eqnarray*}
b_n
&=&\cfrac{1}{\pi}\int_{-\pi}^{\pi}x\sin nxdx\\
&=&\cfrac{2}{\pi}\int_0^{\pi}x\sin nxdx\\
&=&\cfrac{2}{\pi}\big[x(-\cfrac{1}{n}\cos nx)\big]_0^{\pi}- \cfrac{2}{\pi}\int_0^{\pi}\big(-\cfrac{1}{n}\big)\cos nxdx\\
&=&\cfrac{2}{\pi}\cdot \pi(-\cfrac{1}{n}\cos n\pi) + \cfrac{2}{n\pi}\big[\cfrac{1}{n}\sin nx \big]_0^{\pi}\\
&=&-\cfrac{2}{n}(-1)^n \\
&=&\cfrac{2}{n}(-1)^{n+1}
\end{eqnarray*}
$したがって$
$\quad f(x)=2\sin x -\sin 2x +\cfrac{2}{3}\sin 3x -\cfrac{2}{4}\sin 4x + \cdots $
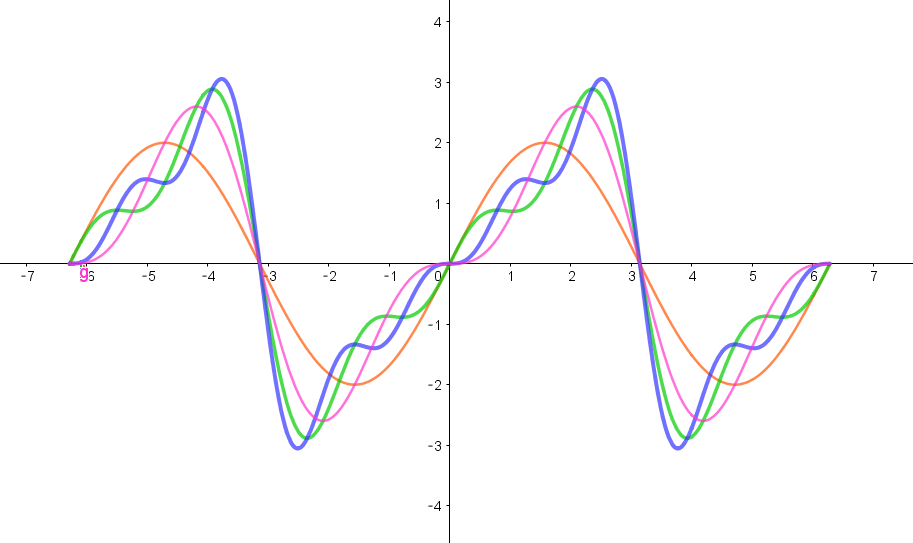
$右図のグラフは、初めの第 \ 1\ 項(基本波)はオレンンジ色、$
$第 \ 2\ 項(第2高調波)までの和は赤色、第 \ 3\ 項(第3高調波)までの和は$
$緑色、第 \ 4\ 項(第4高調波)までの和は青色で示してあります。$
$だんだんノコギリ歯に近づいていくのがわかります。$
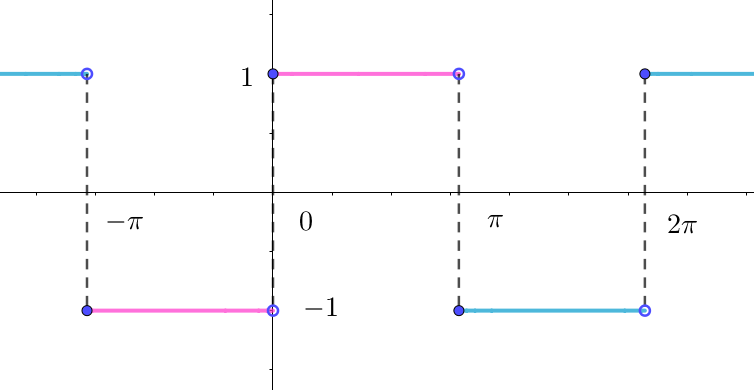
$例2 \quad 右図のグラフのような「矩形波」のフーリェ級数展開を$
$\qquad 求めてみましょう。$
$\quad f(x)\ は周期 \ 2\pi \ の周期関数で$
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
-1 \quad (-\pi \leqq x < 0)\\
1 \qquad (0 \leqq x <\pi)\\
\end{array} \right.
\]
$\quad f(x)\ は奇関数だから \quad a_0=0,\quad a_n=0$
\begin{eqnarray*}
b_n
&=&\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\\
&=&\cfrac{1}{\pi}\big(-\int_{-\pi}^0 \sin nxdx + \int_0^{\pi}\sin nxdx \big)\\
&=&\cfrac{1}{n\pi}\big(\big[\cos nx\big]_{-\pi}^0 - \big[\cos nx\big]_0^{\pi}\big)\\
&=&\cfrac{2}{n\pi}(1-\cos n\pi)\\
&=&\left\{ \begin{array}{l}
\cfrac{4}{n\pi} \hspace{4em}(n=2k-1)\\
0 \hspace{5em}(n=2k)\\
\end{array} \right.
\end{eqnarray*}
$したがって$
$\quad f(x)=\cfrac{4}{\pi}(\sin x +\cfrac{1}{3}\sin 3x +\cfrac{1}{5}\sin 5x + \cdots )$
$ここで、x=\cfrac{\pi}{2} \quad を代入すると \quad f(\cfrac{\pi}{2})=1 \quad だから$
$\qquad 1=\cfrac{4}{\pi}(\sin \cfrac{\pi}{2} +\cfrac{1}{3}\sin \cfrac{3\pi}{2}x +\cfrac{1}{5}\sin \cfrac{5\pi}{2} + \cdots )$
\[1-\cfrac{1}{3}+\cfrac{1}{5} + \cdots = \sum _{n=1}^{\infty} \cfrac{(-1)^{n-1}}{2n-1}=\cfrac{\pi}{4}\]
$これを \ ライプニッツの級数 \ あるいは \ グレゴリーの級数 \ といいます。$
$\hspace{3em} (この級数については($ライプニッツ(グレゴリー)級数$)をご覧ください。)$
4 フーリェ級数の性質
\[定理1 \qquad ||f||^2 \geqq \sum_{i=1}^\infty c_i^2 \qquad (ベッセルの不等式)\]
$(証明)$$\quad ある \ i\ (i=1,\ 2,\ \cdots \ n)\ に対して、直交性により \quad (\varphi _i , \ \varphi _{n+1})=0, \ \ (\varphi _i , \ \varphi _{n+2})=0, \ \cdots \ \ だから$
\[\varphi_i \ は \ \ \sum_{i=n+1}^\infty c_i\varphi_i \ \ に直交する。\] \[\sum_{i=n+1}^\infty c_i\varphi_i =f-f_n \quad だから \quad \varphi_i \perp f-f_n\] \[\varphi_i \ \ の一次結合をとって \quad \sum_{i=1}^n c_i\varphi_i \perp (f-f_n) \qquad \therefore \ \ f_n \perp (f-f_n)\] $\qquad f=f_n+(f-f_n) \quad だから \quad ||f||^2=||f_n||^2+||f-f_n||^2$
\[また \quad ||f_n||^2=||c_1\varphi _1+c_2\varphi _2+ \cdots +c_n\varphi _n||^2 =\sum_{i=1}^n c_i^2||\varphi_i||^2 =\sum_{i=1}^n c_i^2 \quad だから\] \[||f||^2=\sum_{i=1}^n c_i^2+||f-f_n||^2 \hspace{8em}(1) \hspace{20em}\] \[||f-f_n||^2 \geqq 0 \quad より \quad ||f||^2 \geqq \sum_{i=1}^n c_i^2 \] \[n\ は任意の自然数だから \quad ||f||^2 \geqq \sum_{i=1}^\infty c_i^2 \]
$定理2 \qquad パーセバルの等式$
\[f(x)\ のフーリェ級数が収束し、その和が \ f(x)\ に等しくなる必要十分条件は \quad ||f||^2=\sum_{i=1}^\infty c_i^2 \]
\[ベッセルの不等式の証明の(1) \ より \quad ||f-f_n||^2 = ||f||^2-\sum_{i=1}^n c_i^2 \] $\qquad n \rightarrow \infty \quad とすると$
\[\quad [||f-f_n|| \rightarrow 0 \ \Longleftrightarrow \ ||f||^2 = \sum_{i=1}^ \infty c_i^2 \] $\quad すなわち \ f(x)\ のフーリェ級数が収束し、その和が \ f(x)\ に等しくなる必要十分条件は$
\[\quad ||f||^2=\sum_{i=1}^\infty c_i^2 \]
$パーセバルの等式が成り立つとき、正規直交系 \ \{\varphi_n\}\ は完備(完全)であるといいます。$
$このとき、f(x)\ のフーリェ展開式において$
\[f(x)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nx+b_n\sin nx)=\cfrac{\sqrt{2\pi}a_0}{2} \times \cfrac{1}{\sqrt{2\pi}}+\sum_{n=1}^\infty (\sqrt{\pi}a_n \times \cfrac{\cos nx}{\sqrt{\pi}} + \sqrt{\pi}b_n\ \times \cfrac{\sin nx}{\sqrt{\pi}})\] $\qquad c_0=\cfrac{\sqrt{2\pi}a_0}{2} ,\quad c_{2n-1}=\sqrt{\pi}a_n ,\quad c_{2n}=\sqrt{\pi}b_n \quad だから$
\[||f||^2=\sum_{n=1}^\infty c_n^2 =\cfrac{\pi}{2}a_0^2+\sum_{n=1}^\infty (\pi a_n^2 +\pi b_n^2)\] $すなわち$
\[\cfrac{1}{\pi}||f||^2=\cfrac{a_0^2}{2} +\sum_{n=1}^\infty (a_n^2 + b_n^2)\]
$応用例 \ 1$
\[\quad ノコギリ波 \quad f(x)= \hspace{1em} \left\{ \begin{array}{l} x \quad (-\pi < x < \pi)\\ 0 \quad (x=-\pi,\pi)\\ \end{array} \right. \] $\quad は周期 \ 2\pi \ の周期関数で,このフーリェ級数展開は \quad a_0=0,\ \ a_n=0,\ \ b_n=\cfrac{2}{n}(-1)^{n+1} \ \ でした。$
\[一方 ||f||^2=\int_{-\pi}^{\pi}x^2dx=\big[\cfrac{x^3}{3}\big]_{-\pi}^{\pi}=\cfrac{2}{3}\pi^3\] $\quad したがって$
\[\cfrac{1}{\pi} \times \cfrac{2}{3}\pi^3 =\sum_{n=1}^\infty \big\{\cfrac{2}{n}(-1)^{n+1}\big\}^2\] \[\cfrac{2}{3}\pi^2 =4\sum_{n=1}^\infty \cfrac{1}{n^2}\] \[\therefore \ \ \sum_{n=1}^\infty \cfrac{1}{n^2}=\cfrac{\pi^2}{6}\]
$\quad これは、リーマンの \ \ \zeta \ 関数$
$\qquad \zeta(p)=\dfrac{1}{1^p}+\dfrac{1}{2^p}+ \cdots +\dfrac{1}{n^p}+\cdots $
$\quad で、p=2\ の場合です。 他の求め方については(\ $$\zeta(2)の値$$\ )をご覧ください。$
$応用例 \ 2$
\[\quad 矩形波 \quad f(x)= \hspace{1em} \left\{ \begin{array}{l} -1 \quad (-\pi \leqq x < 0)\\ 1 \qquad ( 0 \leqq x < \pi)\\ \end{array} \right. \] \[\quad は周期 \ 2\pi \ の周期関数で,このフーリェ級数展開は \quad a_0=0,\ \ a_n=0,\ b_n= \left\{ \begin{array}{l} \cfrac{4}{n\pi} \hspace{2em}(n=2k-1)\\ 0 \hspace{3em}(n=2k)\\ \end{array} \right. \] $\ \ でした。$
\[一方 ||f||^2=\int_{-\pi}^0 (-1)^2dx+ \int_0^{\pi} 1^2dx =\big[x\big]_{-\pi}^0 + \big[x\big]_0^{\pi}=2\pi\] $\quad したがって$
$\quad \cfrac{1}{\pi} \times 2\pi =\big(\cfrac{4}{\pi}\big)^2\big(\cfrac{1}{1^2}+\cfrac{1}{3^2}+ \cfrac{1}{5^2}+\cdots \big)$
\[\therefore \ \ \cfrac{1}{1^2}+\cfrac{1}{3^2}+ \cfrac{1}{5^2}+\cdots = \sum_{n=1}^\infty \cfrac{1}{(2n-1)^2}= \cfrac{\pi^2}{8}\]
5 狭義フーリェ級数の収束性
$(1)\ \ 区間 \ [-\pi,\ \pi] \ において、関数系 \ \{1,\ \cos nx,\ \sin nx\}\ は直交系をなし、この区間で区分的になめらかな関数$
$\quad 全体の集合において完備である。$
$(2)\ \ f(x) が \ 2\pi \ を周期とする区分的に滑らかな関数ならば、f(x)\ のフーリェ係数 \ a_n,\ b_n \ に対し、フーリェ級数は$
$\quad 収束(ノルムでの二乗平均収束)して、その和は \ f(x)\ に等しい。$
$\quad もう少し正確にいえば、不連続点も含めて$
\[\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nx+b_n\sin nx) = \cfrac{1}{2}\{f(x+0)+f(x-0)\}\hspace{14em}\] $\quad が成りたつ。$
$\quad このあたりの論理の展開や証明はかなりやっかいです。専門書にあたってください。$
メインメニュー に戻る