MY MATH NOTE

正三角形の対称変換の表す行列

　
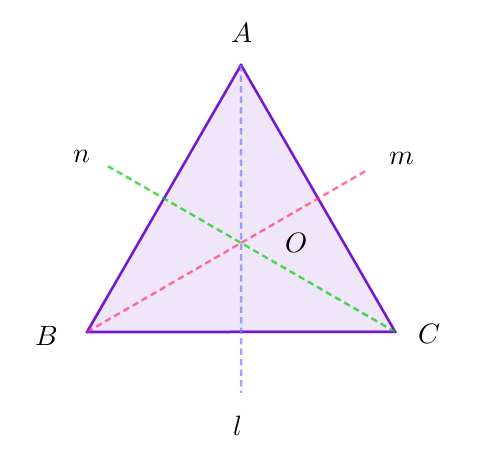
$正三角形ABCの対称変換は、$
$\quad e:恒等変換(そのまま変えない変換)$
$\quad \omega:中心Oのまわりの120°の回転$
$\quad \omega ^2:中心Oのまわりの240°の回転$
$\quad p:l軸に関する折り返し$
$\quad q:m軸に関する折り返し$
$\quad q:n軸に関する折り返し$

$の6通りがあり、頂点の置換で表すと$
\[ e= \left( \begin{array}{rrr} A & B & C\\ A & B & C\\ \end{array} \right) \qquad \omega= \left( \begin{array}{rrr} A & B & C\\ B & C & A\\ \end{array} \right) \qquad \omega ^2= \left( \begin{array}{rrr} A & B & C\\ C & A & B\\ \end{array} \right)\\ \] \[ p= \left( \begin{array}{rrr} A & B & C\\ A & C & B\\ \end{array} \right) \qquad q= \left( \begin{array}{rrr} A & B & C\\ C & B & A\\ \end{array} \right) \qquad r= \left( \begin{array}{rrr} A & B & C\\ B & A & C\\ \end{array} \right) \]
$G=\{e,\ \omega,\ \omega ^2 , \ p,\ q,\ r\}\ \ の演算表は$
\[ \begin{array}{c|c c } \ \times \ &\ e\ &\ \omega\ &\ \omega ^2\ &\ p\ &\ q\ &\ r\\ \hline \ e\ &\ e\ &\ \omega\ &\ \omega ^2\ &\ p\ &\ q\ &\ r\\ \ \omega \ &\ \omega \ &\ \omega ^2\ &\ e\ &\ q\ &\ r\ &\ p\\ \ \omega ^2 \ &\ \omega ^2 \ &\ e \ &\ \omega \ &\ r\ &\ p\ &\ q\\ \ p \ &\ p \ &\ r \ &\ q \ &\ e\ &\ \omega ^2\ &\ \omega \\ \ q \ &\ q \ &\ p \ &\ r \ &\ \omega \ &\ e\ &\ \omega ^2 \\ \ r \ &\ r \ &\ q \ &\ p \ &\ \omega ^2\ &\ \omega \ &\ e \\ \end{array} \]

$置換 \ p,\ q\ の積 \ pq\ は \ p,\ q\ の順に計算しますので、ここでの一次変換 \ P,\ Qについても積 \ PQ\ は$
$この順で計算する必要があります。$

$ところが、一次変換では$
\[ \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) = P \left( \begin{array}{r} x\\ y\\ \end{array} \right) ,\qquad \left( \begin{array}{r} x''\\ y''\\ \end{array} \right) = Q \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) \quad より \quad \left( \begin{array}{r} x''\\ y''\\ \end{array} \right) = QP \left( \begin{array}{r} x\\ y\\ \end{array} \right) \]
$となり、積は順序が \ QP\ となってしまいます。そこで、転置行列をとって$
\[ \left( \begin{array}{rr} x' & y'\\ \end{array} \right) = \left( \begin{array}{rr} x & y\\ \end{array} \right) P' , \qquad \left( \begin{array}{rr} x'' & y''\\ \end{array} \right) = \left( \begin{array}{rr} x' & y' \\ \end{array} \right) Q' \quad とし \qquad \left( \begin{array}{rr} x'' & y''\\ \end{array} \right) = \left( \begin{array}{rr} x & y \\ \end{array} \right) P'Q' \quad とすると\\ \] $一次変換の積は \ P'Q'\ となって置換の積 \ pq\ に対応します。$

$以上のことを踏まえて$

　
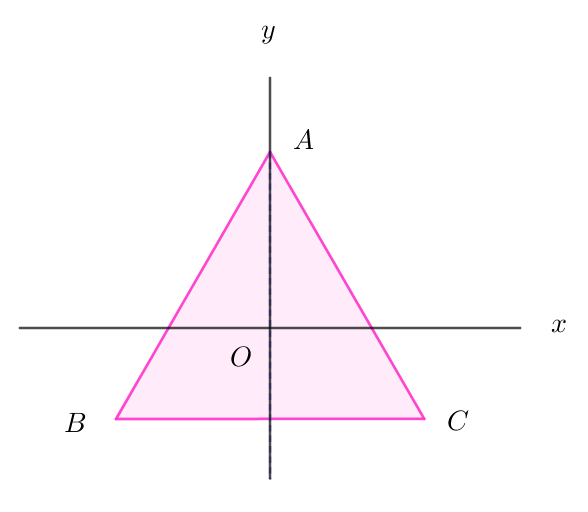
$正三角形の対称変換を一次変換で表すために座標を導入します。$
$右図のように、正三角形の重心を原点とし、BCに平行な直線をx軸とします。$

\[(1)\ \ 原点の回りの角\theta の回転を表す行列は \left( \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\\ \end{array} \right) でしたから \] $\hspace{3em}(一次変換の表す行列は($一次変換の表す行列$)を参照してください。)$

\[この転置をとって \quad \left( \begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\\ \end{array} \right) \quad とします。 \]
$したがって$

$\hspace{3em}$(i)$\ \ 点Oの回りの120°の回転は$
\[ \hspace{3em} W= \left( \begin{array}{rr} \cos 120° & \sin 120°\\ -\sin 120° & \cos 120°\\ \end{array} \right) = \left( \begin{array}{rr} -\small{\dfrac{1}{2}} & \small{\dfrac{\sqrt{3}}{2}}\\ -\small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) \]
$\hspace{3em}$(ii)$\ \ 点Oの回りの240°の回転は$
\[ \hspace{3em} W^2= \left( \begin{array}{rr} \cos 240° & \sin 240°\\ -\sin 240° & \cos 240°\\ \end{array} \right) = \left( \begin{array}{rr} -\small{\dfrac{1}{2}} & -\small{\dfrac{\sqrt{3}}{2}}\\ \small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) \]
\[(2)\ \ 原点を通る直線での折り返しを表す行列は \quad \left( \begin{array}{rr} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta\\ \end{array} \right) \quad でしたが、\\ \]
$\hspace{3em} これは対称行列だからから転置をとっても同じ行列になります。$

　
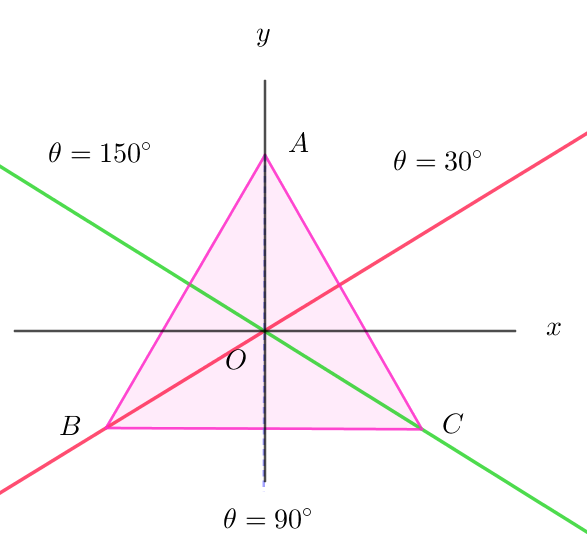
$\hspace{3em}$(iii)$\ \ p:l軸に関する折り返しは \ \ \theta =90 °の場合だから$
\[ \hspace{3em} P= \left( \begin{array}{rr} \cos 180°& \sin 180°\\ \sin 180°& -\cos 180°\\ \end{array} \right) = \left( \begin{array}{rr} -1 & 0\\ 0 & 1\\ \end{array} \right) \]
$\hspace{3em}$(iv)$\ \ q:m軸に関する折り返しは \ \ \theta =30 °の場合だから$
\[ \hspace{3em} Q= \left( \begin{array}{rr} \cos 60°& \sin 60°\\ \sin 60°& -\cos 60°\\ \end{array} \right) = \left( \begin{array}{rr} \small{\dfrac{1}{2}} & \small{\dfrac{\sqrt{3}}{2}}\\ \small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) \]
$\hspace{3em}$(v)$\ \ r:n軸に関する折り返しは \ \ \theta =150 °の場合だから$
\[ \hspace{3em} R= \left( \begin{array}{rr} \cos 300°& \sin 300°\\ \sin 300°& -\cos 300°\\ \end{array} \right) = \left( \begin{array}{rr} \small{\dfrac{1}{2}} & -\small{\dfrac{\sqrt{3}}{2}}\\ -\small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) \]
$行列の積について、例えば$
\[ QR= \left( \begin{array}{rr} \small{\dfrac{1}{2}} & \small{\dfrac{\sqrt{3}}{2}}\\ \small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) \left( \begin{array}{rr} \small{\dfrac{1}{2}} & -\small{\dfrac{\sqrt{3}}{2}}\\ -\small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) = \left( \begin{array}{rr} -\small{\dfrac{1}{2}} & -\small{\dfrac{\sqrt{3}}{2}}\\ \small{\dfrac{\sqrt{3}}{2}} & -\small{\dfrac{1}{2}}\\ \end{array} \right) =W^2 \] $となります。$

$G'=\{E,\ W,\ W^2,\ P,\ Q,\ R\}の演算表は$

\[ \begin{array}{c|c c } \ \times \ &\ E\ &\ W\ &\ W^2\ &\ P\ &\ Q\ &\ R\\ \hline \ E\ &\ E\ &\ W\ &\ W^2\ &\ P\ &\ Q\ &\ R\\ \ W\ &\ W\ &\ W^2\ &\ E\ &\ Q\ &\ R\ &\ P\\ \ W^2 \ &\ W^2 \ &\ E \ &\ W\ &\ R\ &\ P\ &\ Q\\ \ P \ &\ P \ &\ R \ &\ Q \ &\ E\ &\ W^2\ &\ W \\ \ Q \ &\ Q \ &\ P \ &\ R \ &\ W \ &\ E \ &\ W^2 \\ \ R \ &\ R \ &\ Q \ &\ P \ &\ W^2\ &\ W \ &\ E \\ \end{array} \]
$演算表からG'は群となることがわかります。$

$また、Gの元とG'の元は$

$\quad e \ \ \longleftrightarrow \ \ E,\quad \omega \ \ \longleftrightarrow \ \ W,\quad \omega ^2 \ \ \longleftrightarrow \ \ W^2,\quad p \ \ \longleftrightarrow \ \ P,\quad q \ \ \longleftrightarrow \ \ Q,\quad r \ \ \longleftrightarrow \ \ R$

$ように対応するからGとG'は同型となります。\quad (群の同型については($群の同型$)を参照してください。)$



　

ページの先頭へ↑