MY MATH NOTE

一次変換の表す行列

　
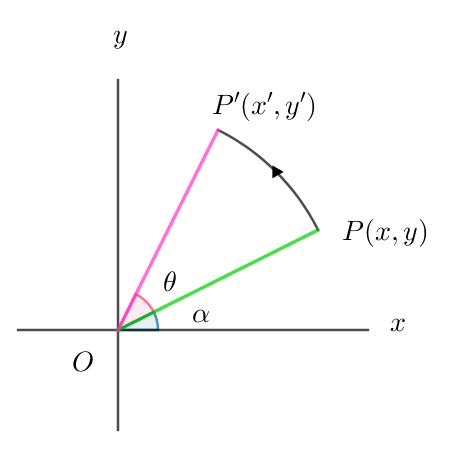
$(1)\ \ 原点の回りの角\theta の回転$

$右図で、OP=r,\quad \angle xOP=\alpha ,\quad 点P(x,y)\ を原点の回りに角 \ \theta \ 回転した点を$
$P'(x',y')\ \ とおくと$

$x=r\cos \alpha , \quad y=r\sin \alpha \ \ だから$
$x'=r\cos (\theta + \alpha)=r\cos \theta \cos \alpha - r\sin \theta \sin \alpha=x\cos \theta -y\sin \theta $
$y'=r\sin (\theta + \alpha)=r\sin \theta \cos \alpha + r\cos \theta \sin \alpha=x\sin \theta +y\cos \theta $

\[ \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) = \left( \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\\ \end{array} \right) \left( \begin{array}{r} x\\ y\\ \end{array} \right) \]

　
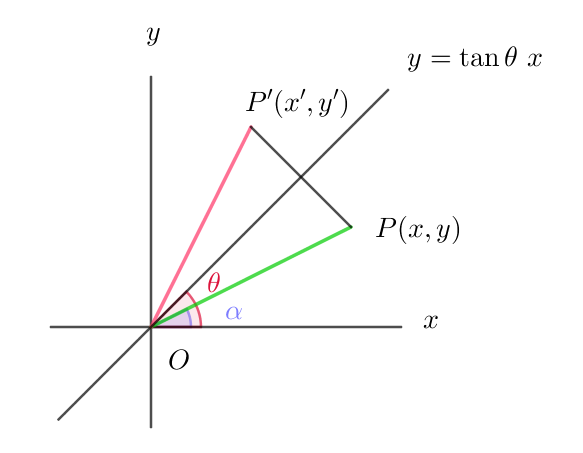
$(2)\ \ 原点を通る傾き \ \tan \theta \ の直線での折返し$

$右図で、OP=r,\quad \angle xOP=\alpha ,\quad 原点を通る直線とx軸の正方向の$
$なす角を \ \theta \ とし、点P(x,y)を折返した点をP'(x',y')\ \ とおくと$

$x=r\cos \alpha , \quad y=r\sin \alpha$
$\angle xOP'=\alpha + 2(\theta -\alpha)=2\theta -\alpha \ \ だから$
$x'=r\cos (2\theta - \alpha)=r\cos 2\theta \cos \alpha + r\sin 2\theta \sin \alpha=x\cos 2\theta +y\sin 2\theta $
$y'=r\sin (2\theta - \alpha)=r\sin 2\theta \cos \alpha - r\cos 2\theta \sin \alpha=x\sin 2\theta -y\cos 2\theta $

\[ \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) = \left( \begin{array}{rr} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta\\ \end{array} \right) \left( \begin{array}{r} x\\ y\\ \end{array} \right) \]

　
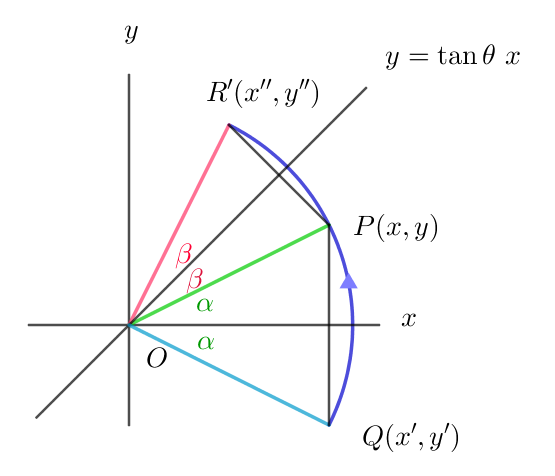
$次のように考えることもできます。$

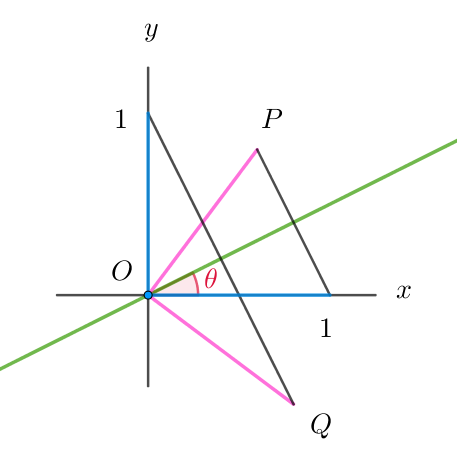
$点P(x,y)の原点を通る傾き \ \tan \theta \ の直線で折返した点R(x'',y'')は$
$点Pのx軸における対称点をQ(x',y')とすると$
$右図からわかるように$
$\theta =\alpha +\beta \ \ で、2\alpha +2\beta =2\theta \ \ だから$
$点Qを原点の回りに角 \ 2\theta \ 回転させると得られます。$
$したがって、$
\[ \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) = \left( \begin{array}{rr} 1 & 0 \\ 0& -1\\ \end{array} \right) \left( \begin{array}{r} x\\ y\\ \end{array} \right) ,\qquad \left( \begin{array}{r} x''\\ y''\\ \end{array} \right) = \left( \begin{array}{rr} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta\\ \end{array} \right) \left( \begin{array}{r} x'\\ y'\\ \end{array} \right) \]
$ゆえに$
\[ \left( \begin{array}{r} x''\\ y''\\ \end{array} \right) = \left( \begin{array}{rr} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta\\ \end{array} \right) \left( \begin{array}{r} 1 & 0 \\ 0& -1\\ \end{array} \right) \left( \begin{array}{r} x\\ y\\ \end{array} \right) = \left( \begin{array}{rr} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta\\ \end{array} \right) \left( \begin{array}{r} x\\ y\\ \end{array} \right) \]

$(別解)$

$一次変換は互いに一次独立な2つのベクトルの移動先で決定されるから、基本ベクトルについて$
$調べればよい。$
$一次変換をTとおくと$

\[ T \left( \begin{array}{r} 1\\ 0\\ \end{array} \right) = \left( \begin{array}{r} a\\ b\\ \end{array} \right) ,\quad T \left( \begin{array}{r} 0\\ 1\\ \end{array} \right) = \left( \begin{array}{r} c\\ d\\ \end{array} \right) \quad ならば \]
\[ T \left( \begin{array}{rr} 1 & 0\\ 0 & 1\\ \end{array} \right) = \left( \begin{array}{rr} a & c\\ b & d\\ \end{array} \right) \quad だから \quad T= \left( \begin{array}{rr} a & c\\ b & d\\ \end{array} \right) \left( \begin{array}{rr} 1 & 0\\ 0 & 1\\ \end{array} \right)^{-1} = \left( \begin{array}{rr} a & c\\ b & d\\ \end{array} \right)\\ \]
$これを利用して、前の2つの一次変換の表す行列をこの方法で求めてみましょう。$

　
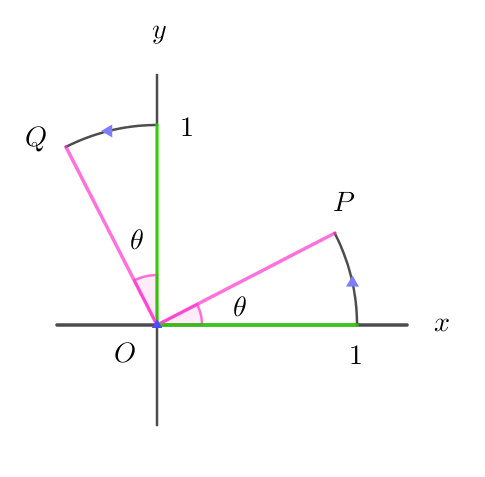
$(1)\ \ 原点の回りの角 \ \theta \ の回転$

$右図のように、基本ベクトル\ \ (1,0),\ \ (0,1)\ \ を角 \ \theta \ 回転させると$
\[ T \left( \begin{array}{r} 1\\ 0\\ \end{array} \right) = \left( \begin{array}{r} \cos \theta \\ \sin \theta\\ \end{array} \right) ,\quad T \left( \begin{array}{r} 0\\ 1\\ \end{array} \right) = \left( \begin{array}{r} -\sin \theta \\ \cos \theta \\ \end{array} \right)\\ \] $だから$
\[ T= \left( \begin{array}{rr} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{array} \right) \]

　
$(2)\ \ 原点を通る傾き \ \tan \theta \ の直線での折返し$

$右図のように、基本ベクトル\ \ (1,0),\ \ (0,1)\ \ を原点を通る傾き \ \ \tan \theta \ の$
$直線で折り返すと$
\[ T \left( \begin{array}{r} 1\\ 0\\ \end{array} \right) = \left( \begin{array}{r} \cos 2\theta \\ \sin 2\theta\\ \end{array} \right) ,\quad T \left( \begin{array}{r} 0\\ 1\\ \end{array} \right) = \left( \begin{array}{r} \cos (2\theta -\cfrac{\pi}{2})\\ \sin (2\theta -\cfrac{\pi}{2})\\ \end{array} \right) = \left( \begin{array}{r} \sin 2\theta \\ -\cos 2\theta\\ \end{array} \right)\\ \] $だから$
\[ T= \left( \begin{array}{rr} \cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \\ \end{array} \right) \]


　

ページの先頭へ↑