群の同型
$演算 \circ \ の群G と演算 \ast\ の群G'\ において、Gの元とG'\ の元は1対1に対応し、 a,b \in G,\quad a',b' \in G' \ \ とする。$
$\qquad a \ \ \longleftrightarrow \ \ a',\quad b \ \ \longleftrightarrow \ \ b' \quad ならば \quad a \circ b \ \ \longleftrightarrow \ \ a'\ast b'$
$が成りたつとき、G とG'\ は同型であるといい、G \simeq G' \ \ とかきます。$
$なお、多対1対応のときは準同型といいます。$
$同型な2つの群GとG'\ には次のような性質があります。$
$(1)\ \ 単位元$
$\quad Gの単位元 \ e\ には \ G'\ の単位元 \ e'\ が対応する。$
$(証明)$
$Gの任意の元をaとし、対応するG'\ の元をa'する。Gの単位元 \ e\ に対応するG'\ の元を \ f\ とすると$
$\qquad a \ \ \longleftrightarrow \ \ a',\quad e \ \ \longleftrightarrow \ \ f\quad だから$
$\qquad e \circ a=a \quad \longleftrightarrow \quad f \ast a'=a'$
$\qquad a \circ e=a \quad \longleftrightarrow \quad a'\ast f=a'$
$よって \quad f\ はG'\ の単位元 \ e'\ である。$
$(2)\ \ 逆元$
$Gの元 \ a\ にG'\ の元 \ a'\ が対応するとき、a\ の逆元 \ a^{-1}\ には \ a'\ の逆元 \ a'^{-1}\ が対応する。$
$(証明)$
$Gの元 \ a^{-1}\ に対応するG'\ の元を \ b とすると$
$\qquad a \ \ \longleftrightarrow \ \ a',\quad a^{-1} \ \ \longleftrightarrow \ \ b\quad だから$
$\qquad a \circ a^{-1}=a' \ast b$
$\qquad 左辺= e\ \ \longleftrightarrow \ \ e' \quad だから \quad a' \ast b=e'$
$同様にして$
$\qquad a^{-1} \circ a=b \ast a'$
$\qquad 左辺=e \ \ \longleftrightarrow \ \ e' \quad だから \quad b \ast a'=e'$
$よって、b= a'^{-1}$
$例$
$f_1(x)=x,\quad f_2(x)=-\cfrac{1}{x},\quad f_3(x)=\cfrac{1+x}{1-x},\quad f_4(x)=-\cfrac{1-x}{1+x} \quad において$
$f_i\ と \ f_j\ の合成 \ f_j(f_i(x))\ を \ f_j \circ f_i \ で表します。$
$\quad 例えば f_2 \circ f_3(x)=f_2(f_3(x))=-\cfrac{1}{\cfrac{1+x}{1-x}}=- \cfrac{1-x}{1+x} \quad だから \ \ f_2 \circ f_3=f_4$
$すべての演算結果をまとめた表は$
\[ \begin{array}{c|c c } \ \circ \ &\ f_1\ &\ f_2\ &\ f_3\ &\ f_4\\ \hline \ f_1\ &\ f_1\ &\ f_2\ &\ f_3\ &\ f_4\\ \ f_2\ &\ f_2\ &\ f_1\ &\ f_4 &\ f_3\\ \ f_3\ &\ f_3\ &\ f_4\ &\ f_1 &\ f_2\\ \ f_4\ &\ f_4\ &\ f_3\ &\ f_2 &\ f_1\\ \end{array} \]
$この表から、\ G=\{f_1,\ f_2,\ f_3\ f_4\}\ \ は演算\circ について群となることがわかります。$
$また$
$長方形の対称変換で(長方形の対称変換は($平面図形の対称変換$)を参照してください。)$
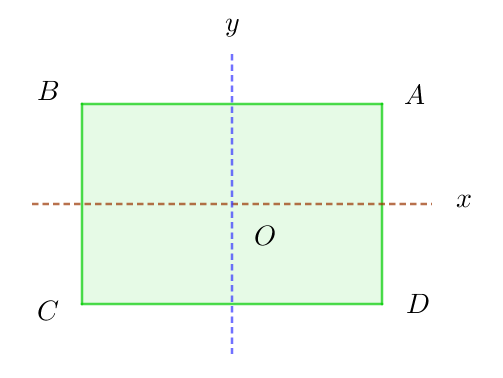
$\quad e:恒等変換(そのまま変えない変換)$
$\quad p:x軸に関する折返し$
$\quad q:y軸に関する折返し$
$\quad r:中心Oのまわりの180°の回転$
$を、元の頂点と移動先の頂点との置換で表すと$
\[
e=
\left(
\begin{array}{rrrr}
A & B & C & D\\
A & B & C & D\\
\end{array}
\right)
\quad
p=
\left(
\begin{array}{rrrr}
A & B & C & D\\
D & C & B & A\\
\end{array}
\right)
\qquad
q=
\left(
\begin{array}{rrrr}
A & B & C & D\\
B & A & D & C\\
\end{array}
\right)
\qquad
r=
\left(
\begin{array}{rrrr}
A & B & C & D\\
C & D & A & B\\
\end{array}
\right)
\]
$変換 \ r\ をおこなってから、さらに続けて変換 \ p\ をおこなうことは、$
\[
r\ p=
\left(
\begin{array}{rrrr}
A & B & C & D\\
C & D & A & B\\
\end{array}
\right)
\left(
\begin{array}{rrrr}
A & B & C & D\\
D & C & B & A\\
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
A & B & C & D\\
B & A & D & C\\
\end{array}
\right)
=q\\
\]
$となって、変換 q\ をおこなったことに一致します。$
$すべての演算結果をまとめた表は$
\[
\begin{array}{c|c c }
\ \times \ &\ e\ &\ p\ &\ q\ &\ r\\
\hline
\ e\ & e & p & q & r\\
\ p\ & p & e & r & q\\
\ q\ & q & r & e & p\\
\ r \ & r & q & p & e\\
\end{array}
\]
$この表から、\ G'=\{e,\ p,\ q,\ r\}\ \ は演算について群となることがわかります。$
$GとG'の演算表から、それぞれの元について、$
$\hspace{3em}f_1 \ \ \longleftrightarrow \ \ e,\quad f_2 \ \ \longleftrightarrow \ \ p,\quad f_3 \ \ \longleftrightarrow \ \ r,\quad f_4 \ \ \longleftrightarrow \ \ r $
$が対応していることがわかります。つまりGとG'は同型ということです。$
$位数(元の個数)4のこの群を、「クラインの四元群」といいます。$
メインメニュー に戻る