MY MATH NOTE

平面図形の対称変換

　
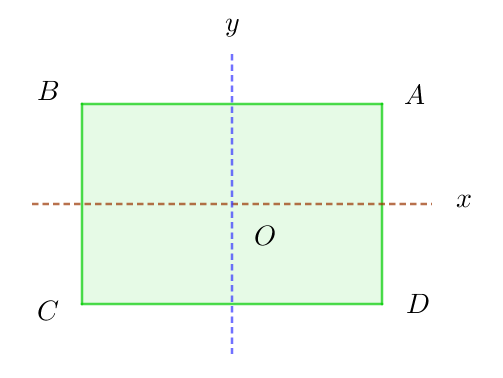
$右図のような長方形ABCDの対称変換は、頂点Aの行き先が決まれば、$
$頂点BはAの隣で2辺の長さの長い方だから1つに決まります。$
$A,Bが決まればC,Dは1通りにきまるので次の4つがあります。$

$\quad e:恒等変換(そのまま変えない変換)$
$\quad \omega:中心Oのまわりの180°の回転$
$\quad p:x軸に関する折返し$
$\quad q:y軸に関する折返し$

$\quad \omega \ \ によって \quad A \rightarrow C,\quad B \rightarrow D,\quad C \rightarrow A,\quad D \rightarrow B \quad に移るから$
\[ \omega= \left( \begin{array}{rrrr} A & B & C & D\\ C & D & A & B\\ \end{array} \right) \quad と表せます。 \] $同様にして$
\[ p= \left( \begin{array}{rrrr} A & B & C & D\\ D & C & B & A\\ \end{array} \right) \qquad q= \left( \begin{array}{rrrr} A & B & C & D\\ B & A & D & C\\ \end{array} \right) \qquad e= \left( \begin{array}{rrrr} A & B & C & D\\ A & B & C & D\\ \end{array} \right) \] $となります。$

　
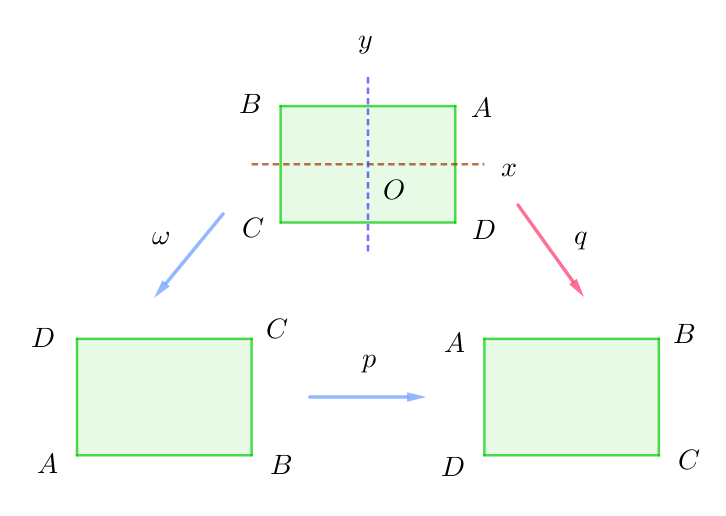
$次に、変換 \ \omega\ をおこなってから、さらに続けて変換 \ p\ を$
$おこなうとどうなるか調べましょう。$

$右図のとおり、\ \omega \ をあらわす置換とp\ を表す置換の$
$積 \ \omega \ p を求めると$

\[ \omega \ p= \left( \begin{array}{rrrr} A & B & C & D\\ C & D & A & B\\ \end{array} \right) \left( \begin{array}{rrrr} A & B & C & D\\ D & C & B & A\\ \end{array} \right)\\ \hspace{2em} = \left( \begin{array}{rrrr} A & B & C & D\\ B & A & D & C\\ \end{array} \right)\\ \] $\hspace{4em}=q$

$となって、変換 q\ をおこなったことに一致することがわかります。$


$長方形の対称変換 \ \ e,\ \omega,\ p,\ q \ \ を繰返しおこなうことは、どのような対称変換をおこなうことと同じか$
$表にまとめてみましょう。これを演算表といいます。$

\[ \begin{array}{c|c c } \ \times \ &\ e\ &\ \omega\ &\ p\ &\ q\\ \hline \ e\ & e & \omega & p　 & q \\ \ \omega \ & \omega & e & q & p\\ \ p\ & p & q & e & \omega\\ \ q\ & q & p & \omega & e\\ \end{array} \]

$(2)\ \ 正三角形の対称変換$

　
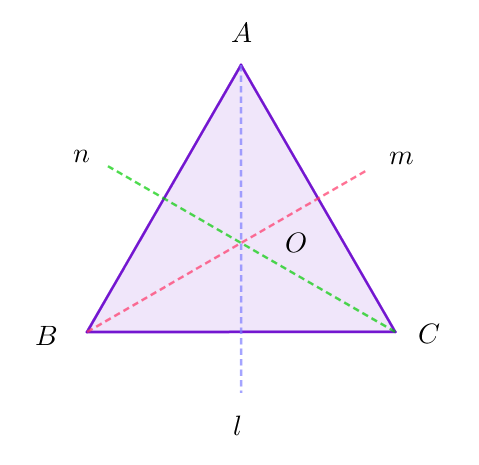
$右図のような正三角形ABCの対称変換は、頂点Aの行き先がきまれば、$
$頂点BはAの隣の2通りがある。A,Bが決まればCは1通りにきまるので$
$全部で3 \times 2=6 \ 通りあります。$

$e:恒等変換(そのまま変えない変換)$
$\omega:中心Oのまわりの120°の回転$
$\omega ^2:中心Oのまわりの240°の回転$
$p:l軸に関する折り返し$
$q:m軸に関する折り返し$
$q:n軸に関する折り返し$

\[ e= \left( \begin{array}{rrr} A & B & C\\ A & B & C\\ \end{array} \right) \qquad \omega= \left( \begin{array}{rrr} A & B & C\\ B & C & A\\ \end{array} \right) \qquad \omega ^2= \left( \begin{array}{rrr} A & B & C\\ C & A & B\\ \end{array} \right)\\ \] \[ p= \left( \begin{array}{rrr} A & B & C\\ A & C & B\\ \end{array} \right) \qquad q= \left( \begin{array}{rrr} A & B & C\\ C & B & A\\ \end{array} \right) \qquad r= \left( \begin{array}{rrr} A & B & C\\ B & A & C\\ \end{array} \right) \]
$演算表は次のとおりです。$

\[ \begin{array}{c|c c } \ \times \ &\ e\ &\ \omega\ &\ \omega ^2\ &\ p\ &\ q\ &\ r\\ \hline \ e\ &\ e\ &\ \omega\ &\ \omega ^2\ &\ p\ &\ q\ &\ r\\ \ \omega \ &\ \omega \ &\ \omega ^2\ &\ e\ &\ q\ &\ r\ &\ p\\ \ \omega ^2 \ &\ \omega ^2 \ &\ e \ &\ \omega \ &\ r\ &\ p\ &\ q\\ \ p \ &\ p \ &\ r \ &\ q \ &\ e\ &\ \omega ^2\ &\ \omega \\ \ q \ &\ q \ &\ p \ &\ r \ &\ \omega \ &\ e\ &\ \omega ^2 \\ \ r \ &\ r \ &\ q \ &\ p \ &\ \omega ^2\ &\ \omega \ &\ e \\ \end{array} \]

$(3)\ \ 正方形の対称変換$

　
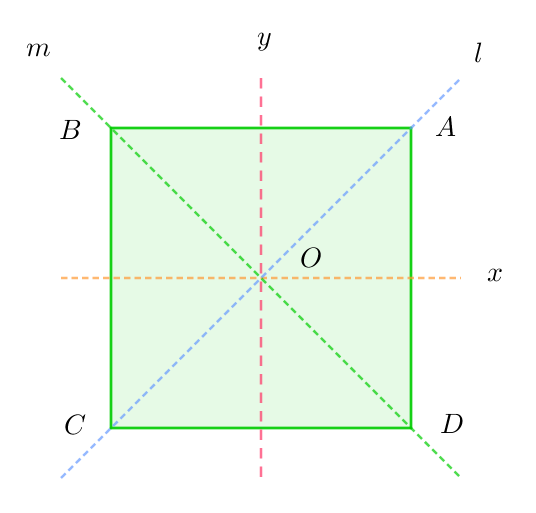
$右図のような正方形ABCDの対称変換は、頂点Aの行き先がきまれば、$
$頂点BはAの隣の2通りがある。A,Bが決まればC,Dは1通りにきまるので$
$全部で4 \times 2=8 \ 通りあります。$

$e:恒等変換(そのまま変えない変換)$
$\omega:中心Oのまわりの90°の回転$
$\omega ^2:中心Oのまわりの180°の回転$
$\omega ^2:中心Oのまわりの270°の回転$
$p:x軸に関する折り返し$
$q:y軸に関する折り返し$
$r:l軸に関する折り返し$
$s:m軸に関する折り返し$

\[ e= \left( \begin{array}{rrrr} A & B & C & D\\ A & B & C & D\\ \end{array} \right) \qquad \omega= \left( \begin{array}{rrrr} A & B & C & D\\ B & C & D & A\\ \end{array} \right) \qquad \omega ^2= \left( \begin{array}{rrrr} A & B & C & D\\ C & D & A & B\\ \end{array} \right) \qquad \omega ^3= \left( \begin{array}{rrrr} A & B & C & D\\ D & A & B & C\\ \end{array} \right)\\ \]
\[ p= \left( \begin{array}{rrrr} A & B & C & D\\ D & C & B & A\\ \end{array} \right) \qquad q= \left( \begin{array}{rrrr} A & B & C & D\\ B & A & D & C\\ \end{array} \right) \qquad r= \left( \begin{array}{rrrr} A & B & C & D\\ A & D & C & B\\ \end{array} \right) \qquad s= \left( \begin{array}{rrrr} A & B & C & D\\ C & B & A & D\\ \end{array} \right)\\ \]
$演算表は省略します。$



　

ページの先頭へ↑