球面極座標表示による曲線の回転体の表面積
$x=x(u,\ v), \ y=y(u,\ v), \ z=z(u,\ v)\ \ (x, \ y, \ z \ \ はそれぞれ \ u,\ v について C^1級)\ のとき$
$\qquad \big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big|= \sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}$
$でした。($曲面積$)をご覧ください。$
$これをつかって、曲線の回転体が球面極座標表示$
$\quad r=r(\theta),\quad x=r\sin \theta \cos \varphi , \quad y=r\sin \theta \sin \varphi,\quad z=r\cos \theta \ \ (0 \leqq \theta \leqq \pi,\ \ 0 \leqq \varphi \leqq 2\pi)$
$されるとき、回転体の表面積を求めます。$
$\quad \cfrac{\partial z}{\partial \varphi}=0 \quad に注意して$
\[\quad \cfrac{\partial (y,\ z)}{\partial (\theta,\ \varphi)}= \left| \begin{array}{ccccc} \cfrac{\partial y}{\partial \theta} & \cfrac{\partial y}{\partial \varphi}\\ \cfrac{\partial z}{\partial \theta} & \cfrac{\partial z}{\partial \varphi}\\ \end{array} \right| =\cfrac{\partial y}{\partial \theta} \cfrac{\partial z}{\partial \varphi} - \cfrac{\partial y}{\partial \varphi} \cfrac{\partial z}{\partial \theta}= -r\sin \theta \cos \varphi (r'\cos \theta -r\sin \theta) \]
\[\quad \cfrac{\partial (z,\ x)}{\partial (\theta,\ \varphi)}= \left| \begin{array}{ccccc} \cfrac{\partial z}{\partial \theta} & \cfrac{\partial z}{\partial \varphi}\\ \cfrac{\partial x}{\partial \theta} & \cfrac{\partial x}{\partial \varphi}\\ \end{array} \right| =\cfrac{\partial z}{\partial \theta} \cfrac{\partial x}{\partial \varphi} - \cfrac{\partial z}{\partial \varphi} \cfrac{\partial x}{\partial \theta}= (r'\cos \theta -r\sin \theta)(-r\sin \theta sin \varphi)\]
\begin{eqnarray*} \cfrac{\partial (x,\ y)}{\partial (\theta,\ \varphi)} &=&\left| \begin{array}{ccccc} \cfrac{\partial x}{\partial \theta} & \cfrac{\partial x}{\partial \varphi}\\ \cfrac{\partial y}{\partial \theta} & \cfrac{\partial y}{\partial \varphi}\\ \end{array} \right| =\cfrac{\partial x}{\partial \theta} \cfrac{\partial y}{\partial \varphi} - \cfrac{\partial x}{\partial \varphi} \cfrac{\partial y}{\partial \theta}\\ \\ &=&(r'\sin \theta +r\cos \theta)\cos \varphi \times r\sin \theta \cos \varphi+ r\sin \theta \sin \varphi \times (r'\sin \theta +r\cos \theta )\sin \varphi\\ \\ &=&r\sin \theta \cos ^2\varphi(r'\sin \theta +r\cos \theta)+r\sin \theta \sin ^2\varphi (r'\sin \theta +r\cos \theta )\\ \\ &=&r\sin \theta (r'\sin \theta +r\cos \theta) \end{eqnarray*}
$したがって$
\begin{eqnarray*} & &\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2\\ \\ &=&r^2\sin ^2\theta \cos ^2\varphi (r'\cos \theta -r\sin \theta)^2 + r^2\sin ^2 \theta sin ^2\varphi(r'\cos \theta -r\sin \theta)^2 +r^2\sin ^2\theta (r'\sin \theta +r\cos \theta)^2\\ \\ &=&r^2\sin ^2\theta (r'\cos \theta -r\sin \theta)^2 + r^2\sin ^2 \theta (r'\sin \theta +r\cos \theta)^2\\ \\ &=&r^2\sin ^2\theta (r'^2\cos ^2\theta -2rr'\sin \theta \cos \theta + r^2\sin ^2 \theta +r'^2\sin ^2\theta +2rr'\sin \theta\cos \theta ++r^2\cos ^2\theta)\\ \\ &=&(r^2+r'^2)r^2 \sin ^2\theta \\ \end{eqnarray*}
$\ 球面極座標表示による曲線の回転体の表面積$
\[ \qquad S=\iint _D \sqrt{r^2+r'^2}\ r \sin \theta \ d\theta \ d\varphi\]
$例1$
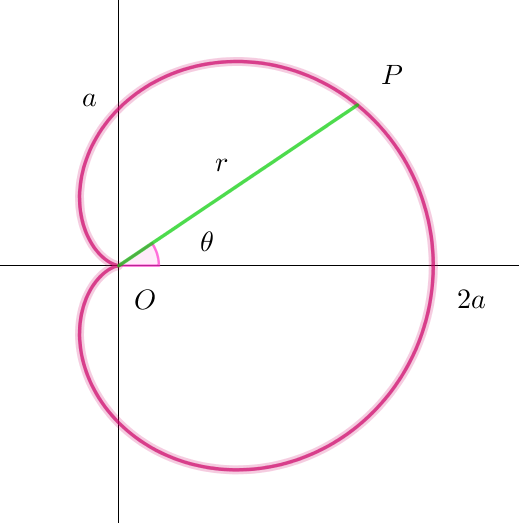
$極座標で表示された曲線 \ \ r=a(1+\cos \theta)\ \ で表される図形を始線の回りに$
$回転してできる回転体の表面積を求めてみましょう。$
$この図形は右図のとおりで、カージオイドとよばれています。$
$\qquad 詳しくは($カージオイド$)をご覧ください。$

$始線を\ z\ 軸として、z軸の回りの回転体は右図のとおりです。$
$回転体上の点 \ P(x,y,z)\ は$
$\quad r=r(\theta),\quad x=r\sin \theta \cos \varphi , \quad y=r\sin \theta \sin \varphi,\quad z=r\cos \theta $
$\qquad (0 \leqq \theta \leqq \pi,\ \ 0 \leqq \varphi \leqq 2\pi) \ \ と表されます。$
$\quad \sqrt{r^2+r'^2}=\sqrt{a^2(1+\cos \theta)^2+(-a\sin \theta)^2}=a\sqrt{2+2\cos \theta}=\sqrt{2}a\sqrt{1+\cos \theta}$
$よって$
\begin{eqnarray*}
S
&=&=\iint _D \sqrt{2}a\sqrt{1+\cos \theta}\ r\ \sin \theta d\theta d\varphi\\
\\
&=&=\iint _D \sqrt{2}a\sqrt{1+\cos \theta}\ a(1+\cos \theta) \sin \theta d\theta d\varphi\\
\\
&=&\sqrt{2}a^2\int _0^{2\pi}\int _0^{\pi} (1+\cos \theta)^{\scriptsize{\cfrac{3}{2}}} \sin \theta d\theta d\varphi\\
\\
&=&\sqrt{2}a^2 \times 2\pi \times \int _0^{\pi} (1+\cos \theta)^{\scriptsize{\cfrac{3}{2}}} \sin \theta d\theta \\
\\
&=&2\sqrt{2}\pi a^2 \big[-\cfrac{2}{5}(1+\cos \theta)^{\scriptsize{\cfrac{5}{2}}}\big]_0^{\pi}\\
\\
&=&2\sqrt{2}\pi a^2 \times \cfrac{2}{5} \times 2^{\scriptsize{\cfrac{5}{2}}}\\
\\
&=&\cfrac{32}{5}\pi a^2
\end{eqnarray*}
回転体の表面積メニュー に戻る
メインメニュー に戻る