カージオイド(心臓形)
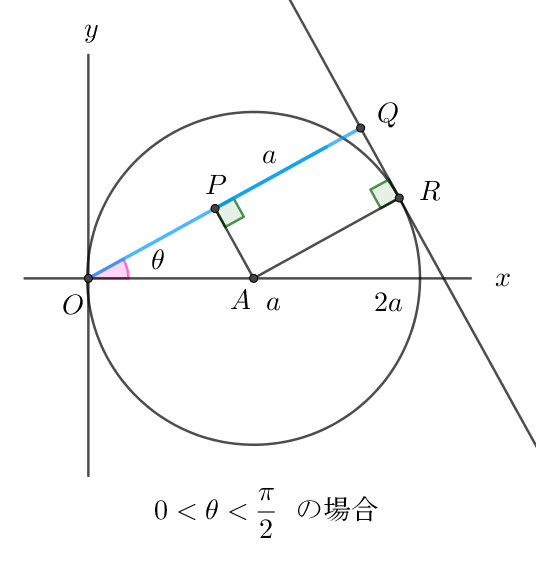
$中心A(a,0),半径aの円周上の点Rで接線lを引くと$
$\qquad l \perp AR$
$原点Oからlに下ろした垂線をOQとする。$
$点AからOQに下ろした垂線をAPとすると$
$四角形ARQPは長方形となる。$
$点Rが円周上を動くとき、点Q(r,\theta )の軌跡(描く曲線 )は$
(i)$\ \ 0 < \theta < \cfrac{\pi}{2} \ \ の場合$
\begin{eqnarray*}
\quad OQ
&=&OP+PQ\\
&=&OP+AR\\
&=&a\cos \theta +a\\
&=&a(1+\cos \theta)\\
\end{eqnarray*}
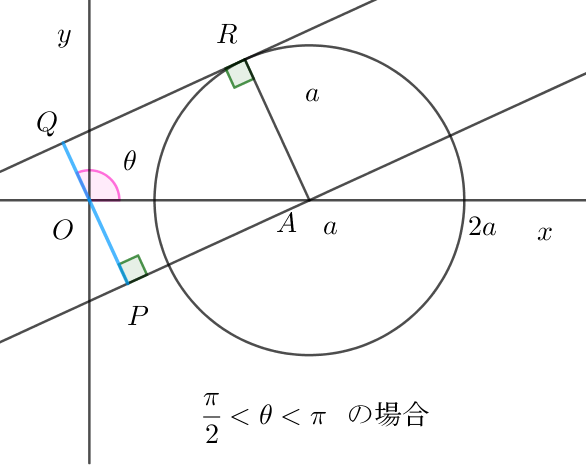
(ii)$\ \ \cfrac{\pi}{2} < \theta < \pi \ \ の場合$
\begin{eqnarray*}
\quad OQ
&=&PQ-OP\\
&=&AR-OP\\
&=&a-a\cos (\pi -\theta)\\
&=&a(1+\cos \theta)\\
\end{eqnarray*}
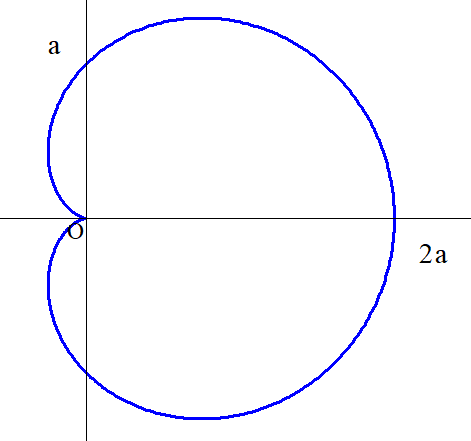
$\pi < \theta < 2\pi \ \ の場合も含めて点Q(r,\theta )の表す方程式は$
(i)$\quad 極方程式は \qquad r=a(1+\cos \theta)$
(ii)$\quad 複素数表示は \qquad z=a(1+\cos \theta)(\cos \theta +i\sin \theta)$
(iii)$\quad パラメータ表示は \quad x=a(1+\cos \theta )\cos \theta ,\quad y=a(1+\cos \theta )\sin \theta$
$グラフは右図です。$
メインメニュー に戻る