曲面積

$領域\ D\ を微小分割して、右図のような微小曲面 \ PQRS\ を考えます。$
$\quad \vec{OP}=\boldsymbol{r}(u,\ v),\quad \vec{OQ}=\boldsymbol{r}(u+\Delta u,\ v),\quad \vec{OR}=\boldsymbol{r}(u+\Delta u,\ v+\Delta v)$
$\quad \vec{OS}=\boldsymbol{r}(u,\ v+\Delta v) \quad だから$
$\vec{PQ}=\boldsymbol{r}(u+\Delta u,\ v) - \boldsymbol{r}(u ,\ v) \fallingdotseq \Delta u \cfrac{\partial \boldsymbol{r}}{\partial u},\qquad
\vec{PS}=\boldsymbol{r}(u,\ v+\Delta v) - \boldsymbol{r}(u ,\ v) \fallingdotseq \Delta v \cfrac{\partial \boldsymbol{r}}{\partial v}$
$微小曲面PQRSの面積 \ \ \Delta S \ \ は$
\begin{eqnarray*}
\Delta S
&\fallingdotseq &平行四辺形PQRS\\
\\
&=&|\vec{PQ} \times \vec{PS}|\\
\\
&=&\big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big|\Delta u \Delta v\\
\end{eqnarray*}
$\Delta u ,\ \ \Delta v \longrightarrow 0 \quad として、分割を細かくしたとき、微小部分の面積の和 \ \ \sum \Delta S \ \ が極限値 \ S\ をもつならば$
$この値を曲面の面積と考えます。$
\[曲面の面積=\iint _D \big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big|\ du dv\]
$\qquad dS=\big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big| \ du dv \quad を面積要素といいます。$
1 x=x(u,v), y=y(u,v), z=z(u,v) (x, y, z はそれぞれ u, v について C1級)のとき
\begin{eqnarray*} & &\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\\ \\ &=& \left| \begin{array}{ccccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k}\\ \cfrac{\partial x}{\partial u} & \cfrac{\partial y}{\partial u} & \cfrac{\partial z}{\partial u} \\ \cfrac{\partial x}{\partial v} & \cfrac{\partial y}{\partial v} & \cfrac{\partial z}{\partial v} \\ \end{array} \right| \\ \\ &=&\big(\cfrac{\partial y}{\partial u} \cfrac{\partial z}{\partial v} - \cfrac{\partial y}{\partial v} \cfrac{\partial z}{\partial u}\big)\boldsymbol{i} +\big(\cfrac{\partial z}{\partial u} \cfrac{\partial x}{\partial v} - \cfrac{\partial z}{\partial v} \cfrac{\partial x}{\partial u}\big)\boldsymbol{j} +\big(\cfrac{\partial x}{\partial u} \cfrac{\partial y}{\partial v} - \cfrac{\partial x}{\partial v} \cfrac{\partial y}{\partial u}\big)\boldsymbol{k} \\ \\ &=&\cfrac{\partial (y,\ z)}{\partial (u,\ v)} \boldsymbol{i}+ \cfrac{\partial (z,\ x)}{\partial (u,\ v)} \boldsymbol{j}+ \cfrac{\partial (x,\ y)}{\partial (u,\ v)} \boldsymbol{k}\\ \end{eqnarray*} \[\qquad ここに \quad \cfrac{\partial (y,\ z)}{\partial (u,\ v)}= \left| \begin{array}{ccccc} \cfrac{\partial y}{\partial u} & \cfrac{\partial y}{\partial v}\\ \cfrac{\partial z}{\partial u} & \cfrac{\partial z}{\partial v}\\ \end{array} \right| =\cfrac{\partial y}{\partial u} \cfrac{\partial z}{\partial v} - \cfrac{\partial y}{\partial v} \cfrac{\partial z}{\partial u} \quad を関数行列式(ヤコビアン)といいます。\]
$したがって次のように表現できます。$
$\big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big|=
\sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}$
$例1$
$\quad 曲面 \ \ \boldsymbol{r}=(av\cos u,\ av\sin u,\ v)\ \ ( a>0,\ \ 0 \leqq u \leqq 2\pi,\ \ 0 \leqq v \leqq 1)\ \ の面積$
$ \qquad この曲面については($曲面$)の例2を参考にしてください。$
$\qquad \cfrac{\partial (y,\ z)}{\partial (u,\ v)}=av\cos u \times 1 - a\sin u \times 0=av\cos u$
$\qquad \cfrac{\partial (z,\ x)}{\partial (u,\ v)}=0 \times a\cos u - 1 \times (-av\sin u )=av\sin u$
$\qquad \cfrac{\partial (x,\ y)}{\partial (u,\ v)}=(-av\sin u) \times a\sin u - a\cos u \times av\cos u =-a^2v\sin ^2u -a^2v \cos ^2u=-a^2v$
$\qquad \sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2} =\sqrt{a^2v^2\cos ^2u +a^2v^2\sin ^2u +a^4v^2}=\sqrt{a^2v^2+a^4v^2}=av\sqrt{1+a^2}$
\begin{eqnarray*} S &=&\iint_Dav\sqrt{1+a^2}dudv\\ \\ &=& a\sqrt{1+a^2} \int _0^{2\pi}du \int _0^1vdv\\ \\ &=& a\sqrt{1+a^2} \times 2\pi \times \big[\cfrac{v^2}{2}\big] _0^1\\ \\ &=&\pi a\sqrt{1+a^2} \end{eqnarray*}
$例2$
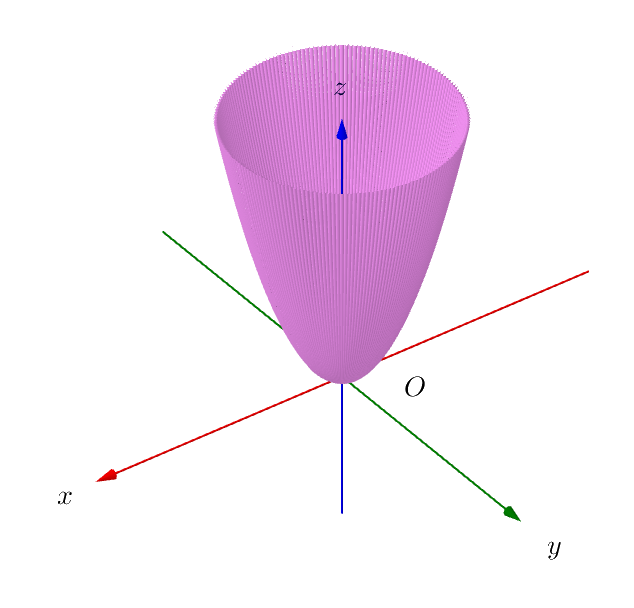
$曲面 \ \ \boldsymbol{r}=(v\cos u,\ v\sin u,\ v^2)\ \ ( 0 \leqq u \leqq 2\pi,\ \ 0 \leqq v \leqq 1)\ \ の面積$
$この曲面は右図のとおりで、回転放物面とよばれています。$
$\quad x^2+y^2=(v\cos u)^2+(v\sin u)^2=v^2=z \quad だから \quad z=x^2+y^2 $
$\quad \cfrac{\partial (y,\ z)}{\partial (u,\ v)}=v\cos u \times 2v - \sin u \times 0=2v^2\cos u$
$\quad \cfrac{\partial (z,\ x)}{\partial (u,\ v)}=0 \times \cos u - 2v \times (-v\sin u )=2v^2\sin u$
$\quad \cfrac{\partial (x,\ y)}{\partial (u,\ v)}=(-v\sin u) \times \sin u - \cos u \times v\cos u =-v\sin ^2u -v \cos ^2u=-v$
$\sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}
=\sqrt{4v^4\cos ^2u +4v^2\sin ^2u +v^2}=\sqrt{4v^4+v^2}=v\sqrt{4v^2+1}$
\begin{eqnarray*}
S
&=&\iint_D v\sqrt{4v^2+1}dudv\\
\\
&=& \int _0^{2\pi}du \int _0^1v\sqrt{4v^2+1}dv\\
\\
&=& 2\pi \times \cfrac{2}{3} \times \big[\cfrac{1}{8}(4v^2+1)^{\scriptsize{\cfrac{3}{2}}}\big] _0^1\\
\\
&=&\cfrac{\pi}{6}(5\sqrt{5}-1)
\end{eqnarray*}
2 z=z(x, y) (zは x, v について C1級)のとき
$\quad u=x,\ \ v=y \quad とおくと \quad z=z(u,v) \quad だから$
$\quad \cfrac{\partial \boldsymbol{r}}{\partial u}=\cfrac{\partial \boldsymbol{r}}{\partial x}=(1,\ 0,\ \cfrac{\partial z}{\partial x}),\qquad \cfrac{\partial \boldsymbol{r}}{\partial v}=\cfrac{\partial \boldsymbol{r}}{\partial y}=(0,\ 1,\ \cfrac{\partial z}{\partial y})$
\[ \cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}= \left| \begin{array}{ccccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k}\\ 1 & 0 & \cfrac{\partial z}{\partial x} \\ 0 & 1 & \cfrac{\partial z}{\partial y} \\ \end{array} \right| =(-\cfrac{\partial z}{\partial x},\ -\cfrac{\partial z}{\partial y},\ 1) \]
$\qquad \big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big|=\sqrt{(-\cfrac{\partial z}{\partial x})^2+(-\cfrac{\partial z}{\partial y})^2+1^2} , \qquad du=dx,\ \ dv=dy \quad だから$
$\qquad dS=\sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}\ dxdy$
\[曲面の面積=\iint _D \sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}\ dxdy\]
曲面の面積メニュー に戻る
メインメニュー に戻る