ラザフォードの散乱公式
1 はじめに
$1911年、ラザフォード(英)はラジウムの放射する\alpha 線(ヘリウムの原子核で正の電荷を帯びている)$
$を金の箔(フォイル)にあてて、散乱される \alpha 粒子の角度分布を調べた。$
$ほとんどの \alpha 粒子は直進するが、中には大きな角度で散乱されるものもあった。この散乱状況から$
$原子は正の電荷をもった核があることがつきとめられた。$
$それでは、ラザフォードの散乱公式をニュートン力学をもちいて導きましょう。$
2 $\alpha$ 粒子の運動
$\hspace{3em}$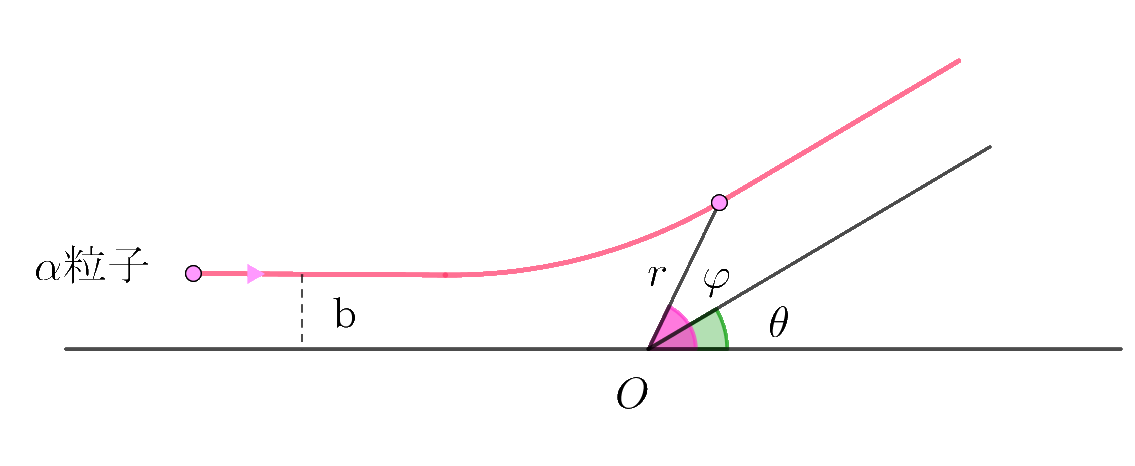
$核を通る軸をx軸とし、これに平行にb離れて入射される\alpha粒子の質量をM,電荷は+2e,$
$入射速度はv_0とする。$
$このbによって\alpha 粒子の軌道が決定されるので、bを衝突パラメータ(径数)という。$
$\alpha 粒子の運動は、核から受けるクーロン力(中心力)であるから、核を始点とする$ 2次元極座標表示 $をつかう。$
(i)$\ r方向の運動方程式は$
$\qquad M\{\cfrac{d^2r}{dt^2}-r\big(\cfrac{d\varphi}{dt}\big)^2\}=\cfrac{2Ze^2}{4\pi\epsilon_0r^2} より$
$\qquad \cfrac{d^2r}{dt^2}-r\big(\cfrac{d\varphi}{dt}\big)^2=\cfrac{2Ze^2}{4\pi\epsilon_0Mr^2} \hspace{15em}(1)$
(ii)$\ \varphi 方向の運動方程式は$
$\qquad M\{2\cfrac{dr}{dt}\cfrac{d\varphi}{dt}+r\cfrac{d^2\varphi}{dt^2}\}=0$
$\qquad M\cfrac{d}{dt}\big(r^2\cfrac{d\varphi}{dt}\big)=0$
よって
$\qquad Mr^2\cfrac{d\varphi}{dt}=L\quad (定数) \hspace{17em} (2)$
$これは角運動量保存を示している。$
$\alpha 粒子の入射時の角運動量は L=-Mv_0b だから$
$\qquad Mr^2\cfrac{d\varphi}{dt}=-Mv_0b $
$\qquad r^2\cfrac{d\varphi}{dt}=-v_0b \hspace{20em}(3)$
$ここで、u=\cfrac{1}{r} と変換すると$
$\qquad \cfrac{d\varphi}{dt}=-\cfrac{v_0b}{r^2}=-v_0bu^2 $
$\qquad \therefore \cfrac{dr}{dt}=\cfrac{d\varphi}{dt}\cfrac{dr}{d\varphi}=-v_0bu^2\cfrac{dr}{d\varphi} \hspace{14em}(4)$
また
$\qquad \cfrac{d}{d\varphi}\big(\cfrac{1}{u}\big)=\cfrac{d}{du}\Big(\cfrac{1}{u}\Big)\cfrac{du}{d\varphi}=-\cfrac{1}{u^2}\cfrac{du}{d\varphi} \hspace{12em} (5)$
\begin{eqnarray*} \cfrac{d^2r}{dt^2}&=&\cfrac{d}{dt}\Big(\cfrac{dr}{dt}\Big)\\ &=&\cfrac{d}{dt}\big(-v_0bu^2\cfrac{dr}{d\varphi}\big) \hspace{8em} (4) より\\ &=&\cfrac{d}{dt}\big\{-v_0bu^2\cfrac{d}{d\varphi}\Big(\cfrac{1}{u}\Big)\Big\}\\ &=&\cfrac{d}{dt}\Big\{-v_0bu^2\big(-\cfrac{1}{u^2}\cfrac{du}{d\varphi}\big)\Big\} \hspace{4em}(5)より\\ &=&\cfrac{d}{dt}\big(v_0b\cfrac{du}{d\varphi}\big)\\ &=&\cfrac{d\varphi}{dt}\cfrac{d}{d\varphi}\big(v_0b\cfrac{du}{d\varphi}\big)\\ &=&-v_0bu^2\cfrac{d}{d\varphi}\big(v_0b\cfrac{du}{d\varphi}\big)\\ &=&-v_0^2b^2u^2\cfrac{d^2u}{d\varphi^2} \hspace{19em}(6)\\ \end{eqnarray*}
$ここで、元にもどって、(3)を(1)に代入すると$
$\qquad \cfrac{d^2r}{dt^2}-\cfrac{1}{r^3}(-v_0b )^2=\cfrac{2Ze^2}{4\pi\epsilon_0Mr^2}$
$(6)を代入して$
$\qquad -v_0^2b^2u^2\cfrac{d^2u}{d\varphi^2}-v_0^2b^2u^3=\cfrac{2Ze^2}{4\pi\epsilon_0M}u^2$
$\qquad \cfrac{d^2u}{d\varphi^2}=-\big(u+\cfrac{2Ze^2}{4\pi\epsilon_0 Mv_0^2b^2}\big)$
$ここで、\cfrac{Ze^2}{4\pi\epsilon_0}=k,\quad \cfrac{1}{2}Mv_0^2=E とおくと$
$\qquad \cfrac{d^2u}{d\varphi^2}=-\big(u+\cfrac{k}{Eb^2}\big) \hspace{18em}(7)$
$右辺第2項は定数であることに注意して p=u+\cfrac{k}{Eb^2} とおくと$
$\qquad \cfrac{d^2p}{d\varphi^2}=-p$
$これは超有名な単振動の微分方程式で、解は$
$\qquad p=A\cos(\varphi + \beta)$
$\qquad \therefore \cfrac{1}{r}=A\cos(\varphi +\beta )-\cfrac{k}{Eb^2} \hspace{16em}(8)$
$ここで、\beta \ を決めるためにtで微分すると$
$\qquad -\cfrac{1}{r^2}\cfrac{dr}{dt}=-A\sin(\varphi +\beta )\cfrac{d\varphi}{dt}$
\begin{eqnarray*} \cfrac{dr}{dt}&=&A\sin(\varphi +\beta ) \times r^2\cfrac{d\varphi}{dt}\\ &=&A\sin(\varphi + \beta ) \times (-v_0b) \hspace{4em} (3)より\\ \\ &=&-Av_0b\sin(\varphi + \beta ) \hspace{16em}(9)\\ \end{eqnarray*}
$ここで、放射側は r \rightarrow \infty ,\quad \varphi=\pi ,\quad \cfrac{dr}{dt}=-v_0 だから$
$(8)式は 0=A\cos(\pi +\beta)-\cfrac{k}{Eb^2} $
$\qquad A\cos \beta =-\cfrac{k}{Eb^2} \hspace{19em}(10)$
$(9)式は -v_0=-Av_0b\sin(\pi + \beta ) $
$\qquad Ab\sin \beta =-1 \hspace{20em}(11)$
$(11) ÷ (10) $
$\qquad \tan \beta = \cfrac{E}{k}b \hspace{21em}(12)$
$これで、\alpha 粒子の軌道が決定されました。$
3 衝突パラメータbと散乱角 $\theta $の関係$
$(8)式の \cfrac{1}{r}=A\cos(\varphi +\beta )-\cfrac{k}{Eb^2} において $
(i)$\ 放射側で r \rightarrow \infty とすると \varphi=\pi だから$
$\qquad 0=A\cos (\pi+\beta ) -\cfrac{k}{Eb^2} $
$\qquad A\cos (\pi+\beta ) =\cfrac{k}{Eb^2} \hspace{19em}(13)$
(ii)$\ 散乱側で r \rightarrow \infty とすると \varphi=\theta だから$
$\qquad 0=A\cos (\theta +\beta ) -\cfrac{k}{Eb^2} \hspace{17em}(14)$
$(14)-(13)より$
$\qquad A\cos (\theta +\beta ) - A\cos (\pi+\beta ) =0$
$\qquad -2A\sin \Big(\beta +\cfrac{\theta}{2}+\cfrac{\pi}{2} \Big)\sin \Big(\cfrac{\theta}{2}-\cfrac{\pi}{2}\Big)=0$
(i) $\sin \Big(\cfrac{\theta}{2}-\cfrac{\pi}{2}\Big)=0 のとき$
$\qquad \cos \cfrac{\theta}{2}=0 \qquad 0 \leqq \theta \leqq \pi だから$
$\qquad \cfrac{\theta}{2}=\cfrac{\pi}{2} \quad \therefore \theta=\pi$
$これは、\alpha 粒子が核の中心に衝突して完全に押し戻される場合であるから、b=0 のときである。$
(ii) $\ \sin \big(\beta +\cfrac{\theta}{2}+\cfrac{\pi}{2} \big)=0 のとき$
$ここで (8)の \cfrac{1}{r}=A\cos(\varphi +\beta )-\cfrac{k}{Eb^2} のAについて \ A < 0 とすると$
$(10)より A\cos \beta < 0 だから \cos \beta > 0$
$(11)より A\sin \beta < 0 だから \sin \beta > 0$
$よって 0 < \beta < \cfrac{\pi}{2}\hspace{20em}(15)$
$また 0 \leqq \theta \leqq \pi だから$
$\qquad \cfrac{\pi}{2} < \beta + \cfrac{\theta}{2} +\cfrac{\pi}{2} < \cfrac{\pi}{2}+\cfrac{\pi}{2}+\cfrac{\pi}{2}$
$したがって$(ii)$の解は \beta +\cfrac{\theta}{2}+\cfrac{\pi}{2} =\pi$
$\qquad \beta = \cfrac{\pi}{2}-\cfrac{\theta}{2} $
$このとき \tan \beta =\tan \big(\cfrac{\pi}{2}-\cfrac{\theta}{2}\big)=\cot \cfrac{\theta}{2} $
$これを(12)に代入すると$
$\qquad \cfrac{E}{k}b =\cot \cfrac{\theta}{2} $
$\qquad \therefore b=\cfrac{k}{E}\cot \cfrac{\theta}{2} \hspace{20em}(16)$
4 ラザフォードの公式
$\hspace{3em}$
 $入射側では、同一の入射速度(エネルギー)をもった多数の\alpha 粒子が送り込まれる。$
$入射側では、同一の入射速度(エネルギー)をもった多数の\alpha 粒子が送り込まれる。$$そこで、単位時間、単位面積当たりに入射する\alpha 粒子の個数をN_0とする。$
$半径bとb+dbの間のリングのうち、中心角がd\varphi の部分の面積は b\ db\ d\varphi だから$
$この領域を通過する \alpha 粒子の個数は dN=N_0b\ db\ d\varphi $
$一方、散乱側では\alpha 粒子は放射状に広がる。原子核の位置を原点Oとした幅rd\theta の帯状の立体角は$
$\hspace{36em}$ 立体角を参照
$\qquad \cfrac{2\pi r \sin \theta \ r\ d\theta}{r^2}=2\pi \sin \theta d\theta$
$であるから、入射側の中心角d\varphi に対する領域の立体角は$
$\qquad d\omega =2\pi\sin \theta d\theta \times \cfrac{d\varphi}{2\pi}=\sin \theta \ d\theta \ d\varphi$
$となる。$
$散乱側の、単位時間、単位立体角当たりの散乱粒子の個数を\sigma(\theta) とするとその個数は$
$\qquad dN=N_0\sigma(\theta)\sin \theta \ d\theta \ d\varphi$
$これらの領域を通過する入射側と散乱側の粒子数は等しいから$
$\qquad dN=N_0b\ db\ d\varphi= N_0\sigma(\theta)\sin \theta \ d\theta \ d\varphi$
$\qquad \therefore \sigma(\theta)=\cfrac{b}{\sin \theta }\times \cfrac{db}{d\theta}$
$(16)より$
$\qquad b=\cfrac{k}{E}\cot \cfrac{\theta}{2}=\cfrac{k}{E}\ \cfrac{1}{\tan \cfrac{\theta}{2}} だから$
\begin{eqnarray*} \cfrac{db}{d\theta}&=&\cfrac{k}{E}\Big(-\cfrac{\cfrac{1}{2} \times \cfrac{1}{\cos ^2\cfrac{\theta}{2}}}{\tan^2{\cfrac{\theta}{2}}}\Big)\\ &=&-\cfrac{k}{2E} \times \cfrac{1}{\tan^2 \cfrac {\theta}{2}\cos ^2\cfrac{\theta}{2}}\\ &=&-\cfrac{k}{2E} \times \cfrac{1}{\sin ^2\cfrac{\theta}{2}}\\ \end{eqnarray*} $これが負になるのは、\cfrac{db}{d\theta} < 0 だからである。$
$そこで、絶対値をとると$
\begin{eqnarray*} \sigma(\theta)&=&\cfrac{k}{E}\ \cfrac{1}{\tan \cfrac{\theta}{2}} \times \cfrac{1}{\sin \theta}\times \Big(\cfrac{k}{2E} \times \cfrac{1}{\sin ^2\cfrac{\theta}{2}}\Big)\\ &=&\cfrac{k^2}{2E^2} \times \cfrac{\cos \cfrac{\theta}{2}}{\sin \cfrac{\theta}{2}} \times \cfrac{1}{2\sin \cfrac{\theta}{2}\cos \cfrac{\theta}{2}}\times \cfrac{1}{\sin ^2\cfrac{\theta}{2}}\\ &=&\cfrac{k^2}{4E^2} \ \cfrac{1}{\sin ^4\cfrac{\theta}{2}}\\ \end{eqnarray*}
$これが有名な「ラザフォードの散乱公式」とよばれている式であり、\sin^4\cfrac{\theta}{2}\ に反比例$
$していることがわかります。$
$散乱された\alpha 粒子は、途中に置かれた蛍光スクリーンにぶつかり発光するすることから$
$これを数えて、理論値 \ \sin ^4\cfrac{\theta}{2} \ に反比例することを確認したわけです。$
$この式もラザフォード自身が導いたというから、やはり歴史に名を残すような偉人はすごいですね。$
5 $\alpha$粒子の描く曲線
$(8)式の \cfrac{1}{r}=A\cos(\varphi +\beta )-\cfrac{k}{Eb^2} より$
$\qquad r=-\cfrac{1}{\cfrac{k}{Eb^2}-A\cos(\varphi +\beta )}=-\cfrac{\cfrac{Eb^2}{k}}{1-\cfrac{Eb^2}{k}A\cos(\varphi +\beta )}$
$これは、2次曲線の極座標表示であることに注意して 離心率 e=-\cfrac{Eb^2}{k}A を求めると$
$(10)式 A\cos \beta =-\cfrac{k}{Eb^2} より A=-\cfrac{k}{Eb^2\cos \beta } を代入して$
$\qquad e=-\cfrac{Eb^2}{k} \times \big(-\cfrac{k}{Eb^2\cos \beta }\big)=\cfrac{1}{\cos \beta}$
$\qquad 0 < \beta < \cfrac{\pi}{2} だから 0 < \cos \beta < 1$
$したがって e>1 となり、双曲線であることが示された。$
$実際は、大量の\alpha 粒子が打ち込まれるわけだから、x軸の回りの回転双曲面となります。$
メインメニュー に戻る