立体角
1 はじめに
$ 初期量子力学にラザフォードの散乱公式$(参照)$という角度分布を求める式があります。$
$この式を導く途中で、「立体角」が使われますが、この立体角なるもの、それまでは聞いた$
$こともありませんでした。$
$また、これがガウス積分と結びつくから不思議です。$
$そこで、この立体角について考えてみましょう。$
2 平面角
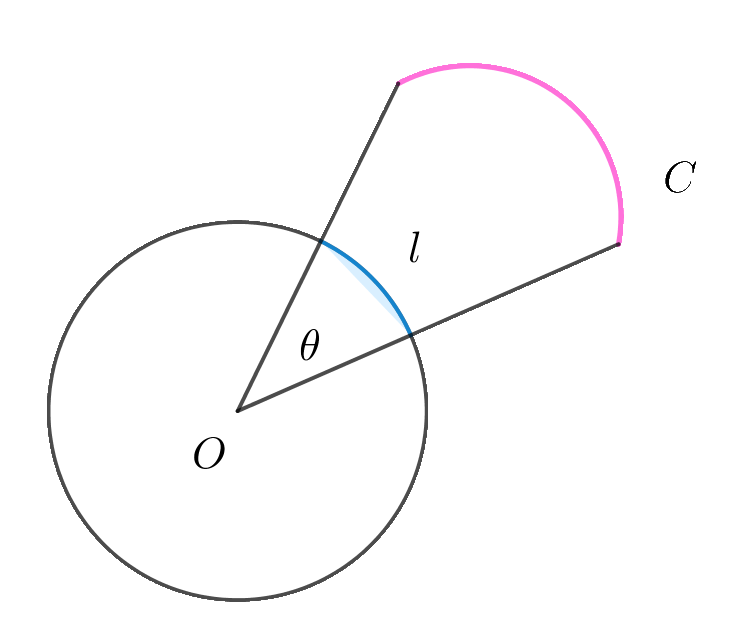
$点Oを中心とする半径\ 1\ の円が切り取る円弧の長さ\ l\ を$
$曲線Cの「平面角」といい、\omega \ であらわす。$
$平面角といっても、2平面のなす幾何的な角度のこと$
$ではない。$
$また、「平面角」と定義したが、この用語はおそらく$
$ないと思われます。$
$立体角をイメージするための私の勝手なネーミングです。$
$例1 半径\ 1\ の円の平面角$
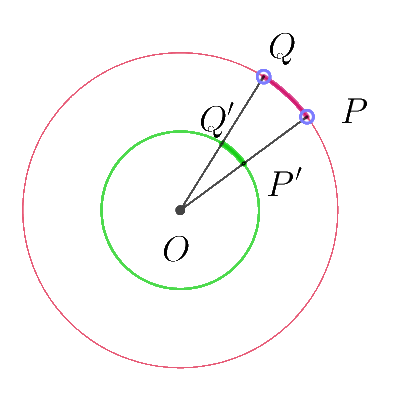
$弧PQを半径\ 1\ の円が切り取ると、弧P'Q'であるが、円周全体では$
$単位円が得られる。$
$よって、平面角は$
$\qquad \omega=1 \times 2\pi =2\pi $
$このことからわかるように、平面角は弧度法(単位はラジアン)を$
$拡張したものと考えてよいでしょう。$
例2 線分の平面角
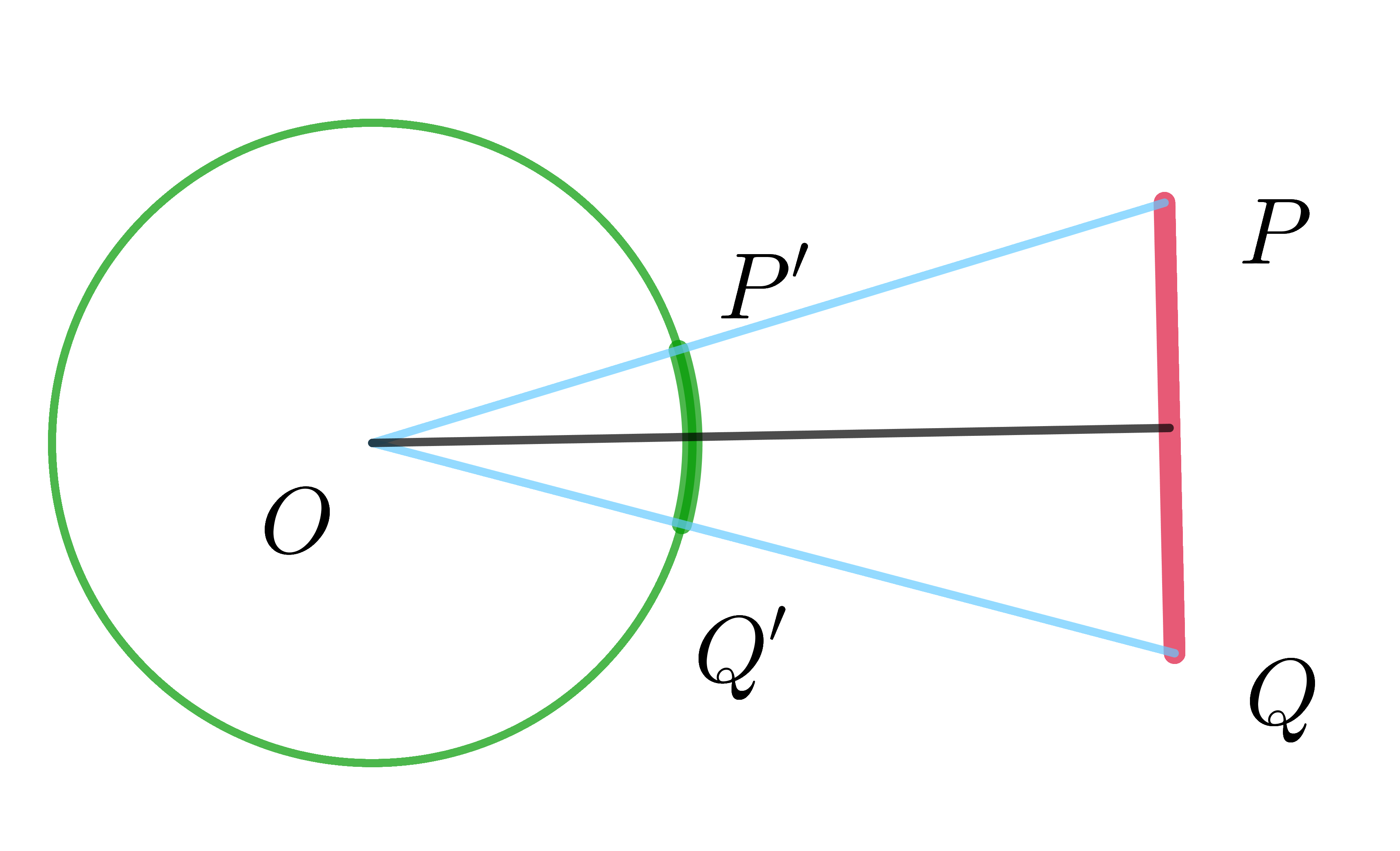
$ただし、線分PQの中点をMとすると$
$\qquad OM=a, \quad OM \perp PQ $
$である。$
$∠POM=\theta \ とすると$
$\\tan \ \theta =\cfrac{\cfrac{b}{2}}{a}=\cfrac{b}{2a} より \theta=\tan ^{-1}\cfrac{b}{2a}$
$よって、平面角は \omega=1 \times 2\theta=2\tan ^{-1}\cfrac{b}{2a}$
$一般の曲線の場合は、微小区間に分割して線分ととらえ、dl=PQとする。$
$PQの法線ベクトルを\ \vec{n},\ PQ上の点Rに対して\vec{OR}=\vec{r} \ とし、\vec{n}\ と\ \vec{r}\ のなす角を \ \theta \ とする。$
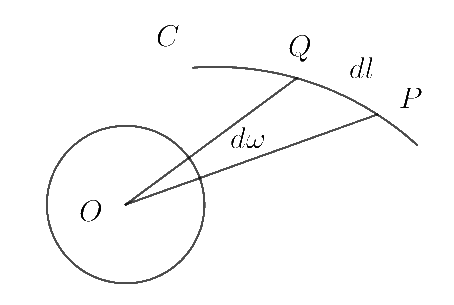
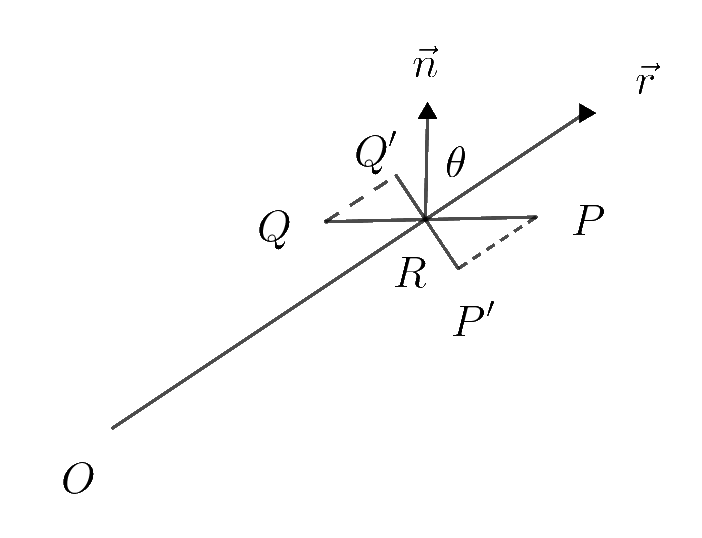
$線分PQの\ \vec{r}\ に垂直な成分P'Q'は \quad P'Q'=PQ\cos \theta =dl\cos \theta $
$線分PQの平面角 \ d\omega \ を用いると相似比が\ 1:r \ であるから \quad P'Q'=rd\omega$
$よって rd\omega=dl\cos \theta$
$\qquad d\omega=\cfrac{\cos \theta}{r}dl=\cfrac{r\cos \theta}{r^2}dl=\cfrac{\vec{r}・\vec{n}}{r^2}dl$
\[\therefore \omega=\int _l \cfrac{\vec{r}・\vec{n}}{r^2}dl\hspace{12em}\]
3 立体角
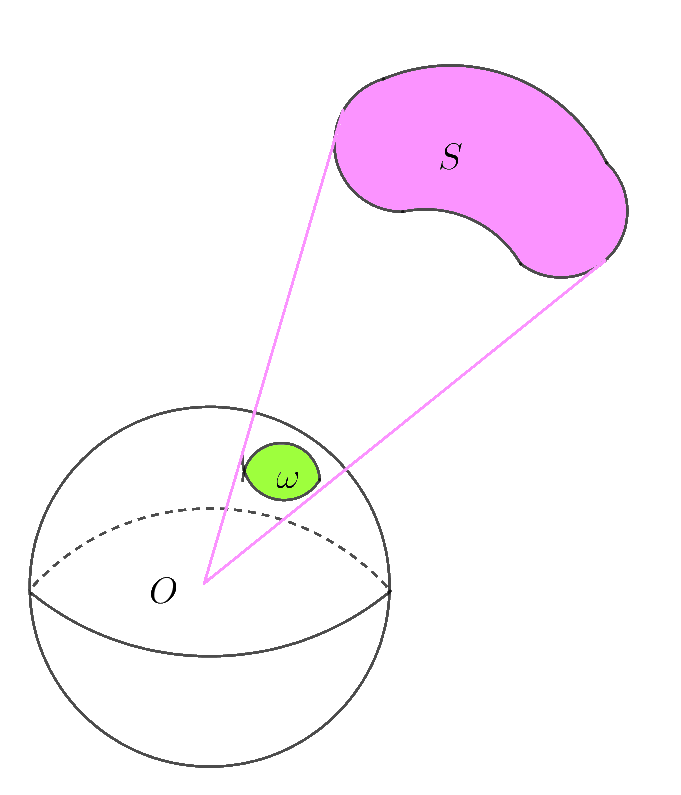
$点Oを中心とする半径\ 1\ の球面が切り取る図形の$
$面積 \ \omega \ を曲面 \ S\ の「立体角」という。$
$とくに、半径 \ r\ の球面が切り取る図形の面積をS(r)とすると$
$面積比は相似比の2乗であるから$
$\qquad \cfrac{\omega}{S(r)}=(\cfrac{1}{r})^2$
$\qquad \therefore \omega=\cfrac{S(r)}{r^2}$
$例1 半径rの球の立体角$
$半径 \ r \ の球の表面積は S(r)=4\pi r^2 $
よって
$\qquad \omega=\cfrac{4\pi r^2}{r^2}=4\pi$
$例2 コンタクトレンズ(球面の一部)の立体角$

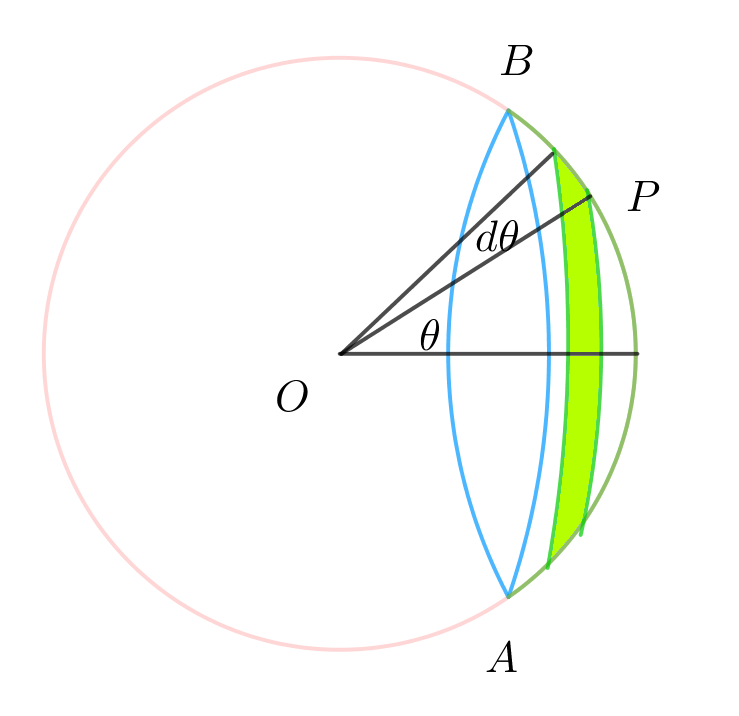
$球面上の点 \ p\ と \ x\ 軸のなす角を \ \theta \ とする。ただし 0 \leqq \theta \leqq \alpha $
$リンゴに包丁をあてて、皮を薄くグルッと剥くイメージで$
$\qquad 幅 \ \ d=rd\theta , 長さ \ \ l=2\pi r\sin \theta だから$
$\qquad 皮の面積は dS=ld=2\pi r\sin \theta \times rd\theta=2\pi r^2\sin \theta d\theta$
よって、立体角は
$\qquad d \omega =\cfrac{dS}{r^2}=2\pi \sin \theta d\theta$
\[\omega=\int _0 ^\alpha d \omega=2\pi\int _0 ^\alpha \sin \theta d \theta=2\pi(1-\cos \alpha)\]
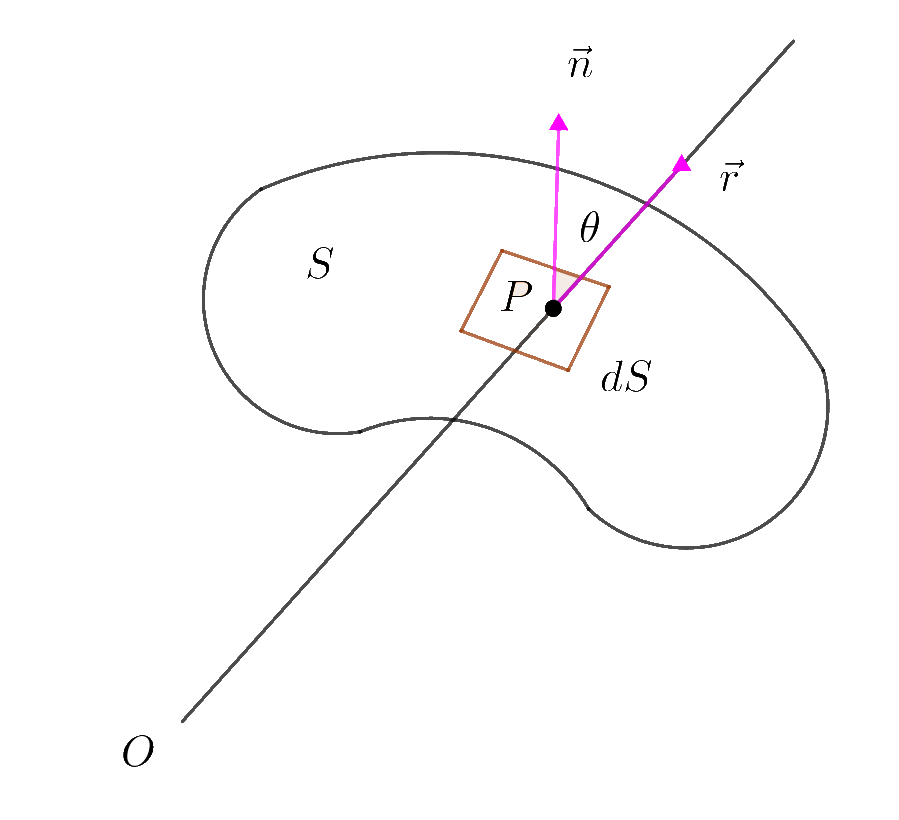
$\vec{OP}\ と向きが一致するが、一般的にはそうならない。$
$そこで、曲面S上の任意の点Pにおける接平面の方向$
$ベクトルを\ \vec{n}, \quad \vec{OP}=\vec{r},\ この2つのベクトルのなす角を$
$\ \theta \ とし、点Pを含む微小曲面の面積をdS とする。$
$r\ 方向の面積は \ dS\cos \theta \ となるから$
$\qquad d\omega =\cfrac{dS\cos \theta }{r^2}=\cfrac{rcos \theta}{r^3}dS=\cfrac{\vec{r}・\vec{n}}{r^3}dS$
$したがって$
\[\hspace{3em} \omega =\iint _S\cfrac{\vec{r}・\vec{n}}{r^3}dS\]
$これを立体角の定義としている本もあるが、初心者には全く理解できない。(私がそうだった!!)$
$上のような手順を踏めば、なんとなくわかったような気がする。(?)$
$とくに、曲面Sとして原点中心、半径 \ r\ の球面をとると、例1より \ \omega =4\pi \ だから$
\[\iint _S\cfrac{\vec{r}・\vec{n}}{r^3}dS=4\pi\] $これを「ガウス積分」といいますが、立体角の考え方から値を導きました。$
$正確には、点OとSの位置関係により$
$\qquad $ガウス積分
$\hspace{2em} 原点O中心、半径 \ r\ の球面をSとすると$
\[
\hspace{3em}
\iint _S\cfrac{\vec{r}・\vec{n}}{r^3}dS=
\begin{cases}
4\pi & (点OがSの内部のとき) \\
0 & (点OがSの外部のとき) \\
2\pi & (点OがS上のとき) \\
\end{cases} \]
$となります。(後ろの2つの証明は次の機会にします)$
$例3\ \ 円板の立体角$
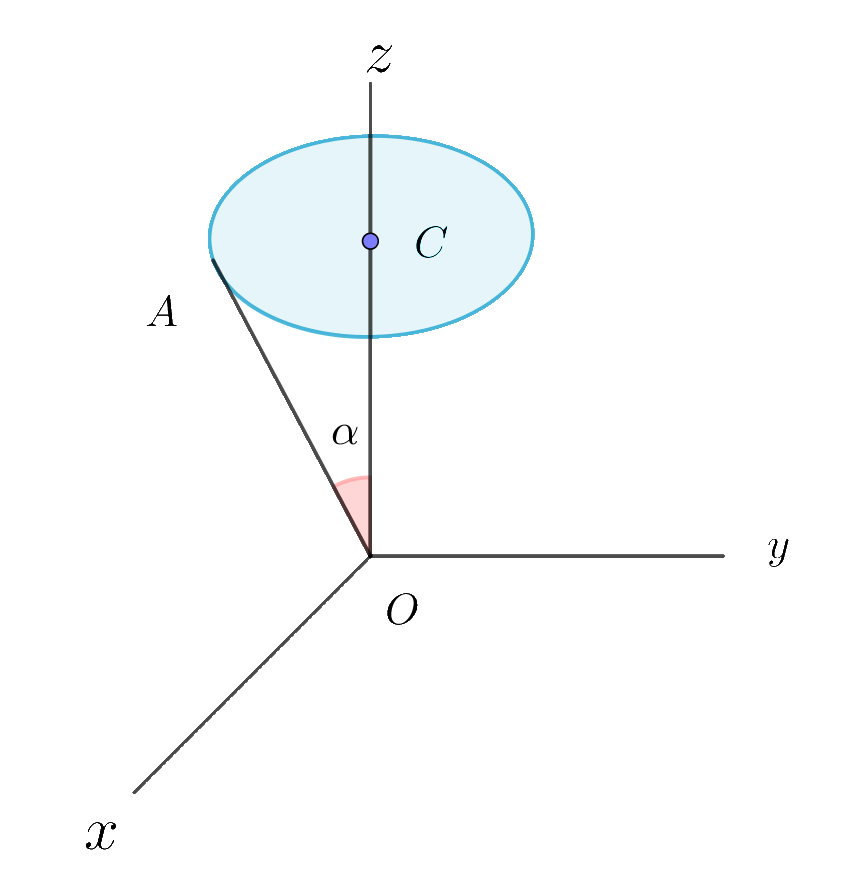
$あり、周上の点をPとすると \ ∠COP=\alpha \ である。$
$OC=l \ とすると \ C(0,0,l)$
$円板状の任意の点をP(x,y,l) ただし x^2+y^2 \leqq a^2 $
$円板の単位法線ベクトルは \ \vec{n}=(0,0,1)$
$とおけるから$
$\qquad \vec{r}・\vec{n}=(x,y,l)・(0,0,1)=l$
$よって$
\[\omega=\iint _S \cfrac{\vec{r}・\vec{n}}{r^3}dS=\iint _S \cfrac{l}{r^3}dS=\iint _S \cfrac{l}{(x^2+y^2+l^2)^\cfrac{3}{2}}dxdy\] $x=\rho\cos \varphi, \ y=\rho\sin \varphi \quad (0 \leqq \rho \leqq a, \ 0 \leqq \varphi \leqq 2\pi)\ と極座標変換すると$
$\qquad x^2+y^2+l^2=\rho^2+l^2,\quad dxdy=\rho d\rho d\varphi $
\begin{eqnarray*} \omega&=&\int_o^{2\pi} \int _0 ^a \cfrac{l}{(\rho ^2+l^2)^{\cfrac{3}{2}}}\rho d\rho d\varphi\\ &=&2\pi l\Big[-(\rho ^2+l^2)^{-\cfrac{1}{2}}\Big]_0^a\\ &=&-2\pi l\Big(\cfrac{1}{\sqrt{a^2+l^2}}-\cfrac{1}{\sqrt{l^2}}\Big)\\ &=&2\pi \Big(1-\cfrac{l}{\sqrt{a^2+l^2}}\Big)\\ &=&2\pi (1-\cos \alpha )\\ \end{eqnarray*}
$例2の結果と一致しましたが、偶然ではありません。$
$曲面Sであろうと円板Cであろうと立体角は等しくなります。$
メインメニュー に戻る