数値積分による$\pi$ の計算

$\hspace{3em}$ 数値積分法とは

　

$(1) \ y=\sqrt{1-x^2} \quad ( 0 \ \leqq x \leqq \ \cfrac{1}{2} \ )\ \ を用いて$
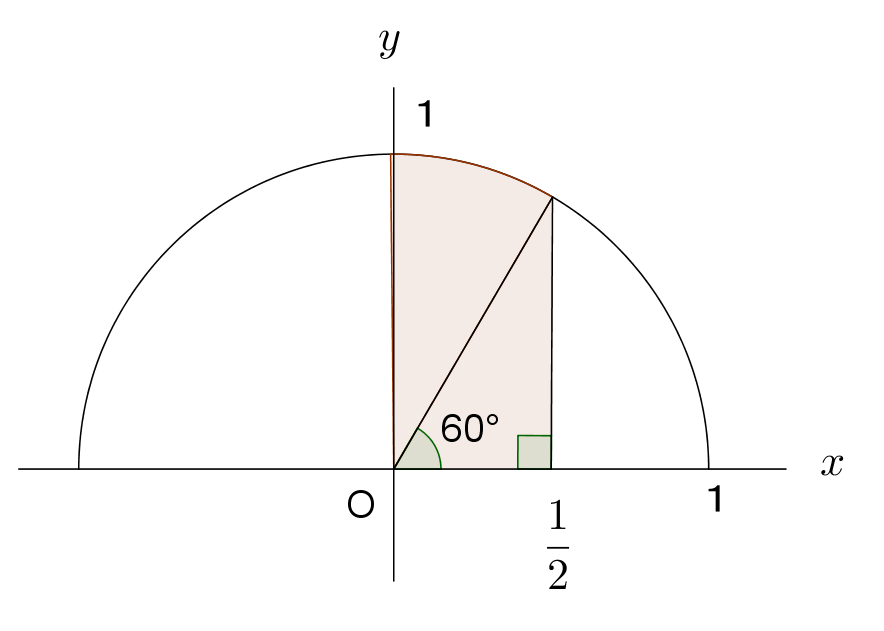
\begin{eqnarray*} I=\int_{0}^{\cfrac{1}{2}}\sqrt{1-x^2} )dx &=&(中心角30°の扇形の面積) + (直角三角形の面積) \hspace{6em}\\ &=&\cfrac{\pi ×1^2}{12} + \cfrac{1}{2} × \cfrac{1}{2} × \cfrac{\sqrt 3}{2}\\ &=&\cfrac{\pi}{12} +\frac{\sqrt 3}{8}\\ \end{eqnarray*} $\hspace{2em} \therefore \ \pi =12I-\cfrac{3}{2}\sqrt 3$

$I$ を数値積分で求めて代入すれば $\pi$ の値が求まる。

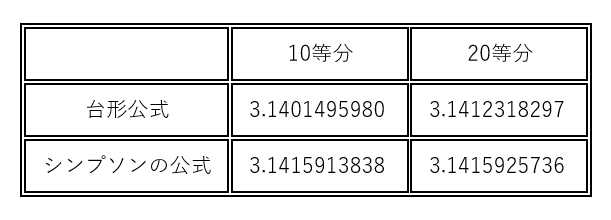
分割数が 10 と 20　のそれぞれについて Excel で計算した結果は下の表のとおりです。
　

　

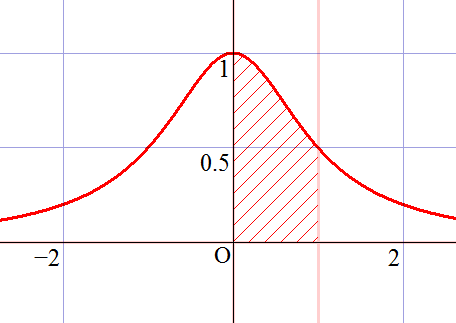
$(2) \ y=\dfrac{1}{1+x^2} \quad ( 0 \ \leqq x \ \leqq \ 1)\ \ を用いて$
\[I=\int_{0}^{1}\dfrac{1}{1+x^2}dx=\left[\tan^{-1}x\right ]_{0}^{1}=\tan^{-1}1=\dfrac{\pi}{4}\] 　だから、$I$ を数値積分で求めて代入すれば $\pi=4I$ より求まる。

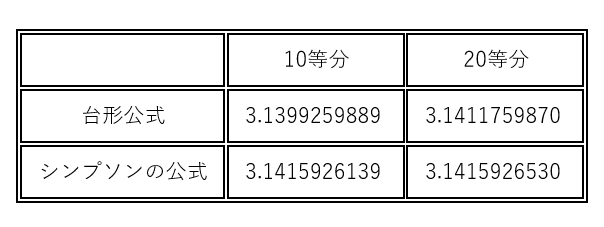
分割数が 10 と 20　のそれぞれについて計算した結果は下の表のとおりです。
　


ページの先頭へ↑




円周率 $π$ の話　に戻る


メインメニュー　に戻る