\[\qquad 不等式 \quad \cfrac{a^p}{p}+\cfrac{b^q}{q} \geqq ab\]


$定理 \quad a > 0,\ \ b > 0,\ \ p > 0,\ \ q > 0,\ \ \cfrac{1}{p}+\cfrac{1}{q}=1 \quad のとき \quad \cfrac{a^p}{p}+\cfrac{b^q}{q} \geqq ab \qquad 等号は \quad a^p=b^q \quad のとき$


$(証明\ 1)$

$\cfrac{1}{p}+\cfrac{1}{q}=1 \quad より \quad p+q=pq \qquad (p-1)(q-1)=1 \qquad \therefore \ \ \cfrac{1}{p-1}=q-1$

$f(x)=x^{p-1}\ \ (p > 1,\ \ x \geqq 0)\quad とおくと \quad x=y^{\scriptsize{\cfrac{1}{p-1}}}=y^{q-1}$

$y=f(x)\ \ は \ \ f(0)=0,\quad x \geqq 0 \quad で単調増加だから、ヤングの不等式( $ ヤングの不等式$をご覧ください) より$

\[\qquad \int _0^a f(x)dx +\int_0^b g(y)dy \geqq ab \]
\[左辺=\int _0^a x^{p-1}dx +\int_0^b y^{q-1}dy =\big[\cfrac{x^p}{p}\big]_0^a +\big[\cfrac{y^q}{q}\big]_0^b=\cfrac{a^p}{p}+\cfrac{b^q}{q}\]
$よって \quad \cfrac{a^p}{p}+\cfrac{b^q}{q} \geqq ab$

$等号は、b=a^{p-1} \ \ のときだから \quad a=b^{\scriptsize{\cfrac{1}{p-1}}}=b^{q-1} \quad すなわち \quad a^p~=b^q \quad のとき$


$(証明 \ 2)$

$f(x)=\cfrac{1}{p}x^p -bx+\cfrac{b^q}{q} \ \ (x > 0)\ \ とおくと \qquad f'(x)=x^{p-1}-b $

\[ f'(x)=0 \quad より \quad x=b^{\scriptsize{\cfrac{1}{p-1}}}=b^{q-1} \qquad 増減表は \qquad \begin{array}{c||c|c|c|c|c} x& 0 & \cdots & b^{q-1} & \cdots \\ \hline f'(x)& & - & 0 & + \\ \hline f(x)& & \searrow & 極小 & \nearrow & \\ \end{array} \]
$f(x)\ は \ x=b^{q-1}\ で極小かつ最小となり、最小値は$
\begin{eqnarray*} f(b^{q-1}) &=&\cfrac{1}{p}(b^{q-1})^p -b\cdot b^{q-1} +\cfrac{b^q}{q} \\ \\ &=&\cfrac{1}{p} b^{pq-p} -b^q +\cfrac{b^q}{q} \\ \\ &=&\cfrac{b^q}{p} -b^q +\cfrac{b^q}{q} \\ \\ &=&\big(\cfrac{1}{p}+\cfrac{1}{q}-1\big)b^q \\ \\ &=&0 \end{eqnarray*} $よって \quad f(x) \geqq f(b^{q-1}) \geqq 0 \quad より \quad \cfrac{1}{p}x^p -bx+\cfrac{b^q}{q} \geqq 0$

$x=a \ \ を代入して \quad \cfrac{1}{p}a^p -ab+\cfrac{1}{q}b^q \geqq 0$

$すなわち　\quad \cfrac{a^p}{p}+\cfrac{b^q}{q} \geqq ab$


$(証明 \ 3)$

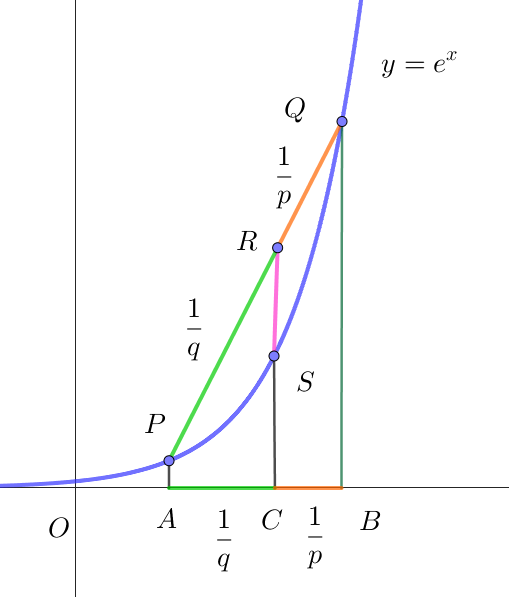　 $f(x)=e^x \quad とおく$

$A(a,\ 0),\ B(b,\ 0) \ \ とし、線分 \ AB\ を \ \ \cfrac{1}{q} : \cfrac{1}{p}\ \ に内分する点を \ C\ とすると$

$\quad C(\cfrac{a}{p}+\cfrac{b}{q},\ 0)$

$3\ 点 \ A,\ B,\ C\ に対応する曲線上の点をそれぞれ \ P,\ Q,\ S\ とし、線分 \ PQ\ を$

$\cfrac{1}{q} : \cfrac{1}{p}\ \ に内分する点を \ R\ とすると、$

$P(a,\ e^a),\ \ Q(b,\ e^b),\ \ S(\cfrac{a}{p}+\cfrac{b}{q}, \ e^{\scriptsize{\cfrac{a}{p}+\cfrac{b}{q}}}),\ \ R(\cfrac{a}{p}+\cfrac{b}{q},\ \cfrac{e^a}{p}+\cfrac{e^b}{q})$

$f(x)=e^x \ \ は下に凸な曲線だから \quad CR \geqq CS \quad (このことについては $ 曲線の凹凸$をご覧ください)$

$\cfrac{e^a}{p}+\cfrac{e^b}{q} \geqq e^{\scriptsize{\cfrac{a}{p}+\cfrac{b}{q}}} \qquad \therefore \ \ \cfrac{e^a}{p}+\cfrac{e^b}{q} \geqq e^{\scriptsize{\cfrac{a}{p}}} \cdot e^{\scriptsize{\cfrac{b}{q}}} $

$e^{\scriptsize{\cfrac{a}{p}}}\ \ と \ \ e^{\scriptsize{\cfrac{b}{q}}}\ \ をあらためて \ \ a,\ b\ \ とおくと \quad e^a=a^p,\quad e^b=b^q \quad だから \quad \cfrac{a^p}{p}+\cfrac{b^q}{q} \geqq ab$

$(証明 \ 4)$

　
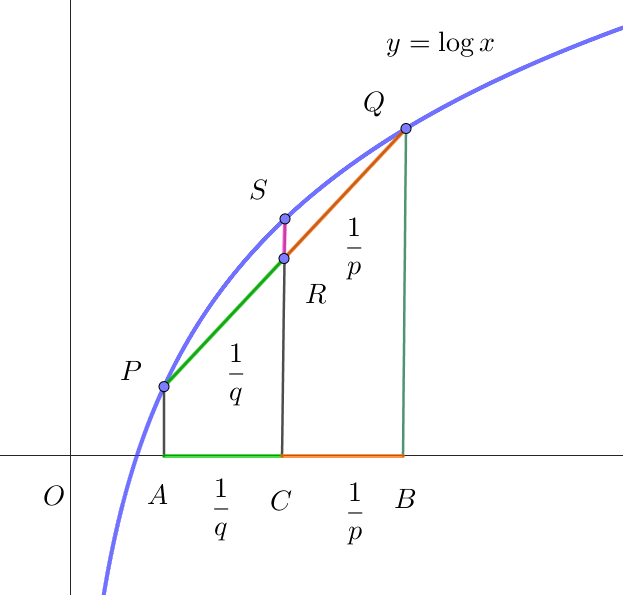
$f(x)=\log x \quad とおく$

$A(a^p,\ 0),\ B(b^q,\ 0) \ とし、線分 \ \ AB \ \ を \ \ \cfrac{1}{q} : \cfrac{1}{p}\ \ に内分する点を \ C\ とすると$

$\quad C(\cfrac{a^p}{p}+\cfrac{b^q}{q},\ 0)$

$3\ 点 \ A,\ B,\ C\ に対応する曲線上の点をそれぞれ \ P,\ Q,\ S \ とし、線分 \ PQ\ を$

$\cfrac{1}{q} : \cfrac{1}{p}\ \ に内分する点を \ R\ とすると$

$\quad P(a^p,\ \log a^p),\ Q(b^q,\ \log b^q),\ S(\cfrac{a^p}{p}+\cfrac{b^q}{q},\ \log \big({\cfrac{a^p}{p}+\cfrac{b^q}{q}}\big)),\ \ R(\cfrac{a^p}{p}+\cfrac{b^q}{q},\ \cfrac{\log a^p}{p}+\cfrac{\log b^q}{q})$

$f(x)=\log x \ \ は上に凸な曲線だから \qquad CR \leqq CS \quad (このことについては $ 曲線の凹凸$をご覧ください)$

$\cfrac{\log a^p}{p}+\cfrac{\log b^q}{q} \leqq \log \big({\cfrac{a^p}{p}+\cfrac{b^q}{q}}\big)$

$\log a + \log b \leqq \log \big({\cfrac{a^p}{p}+\cfrac{b^q}{q}}\big)$

$\log ab \leqq \log \big({\cfrac{a^p}{p}+\cfrac{b^q}{q}}\big)$

$\therefore \ \ ab \leqq {\cfrac{a^p}{p}+\cfrac{b^q}{q}}$


ページの先頭へ↑



メインメニュー　に戻る