ヤングの不等式
$y=f(x)\ は \ \ x \geqq 0\ \ で連続な単調増加関数で、f(0)=0\ \ とする。x=g(y)\ をその逆関数とすると、$
\[a >0,\ \ b>0 \ のとき \quad \int _0^a f(x)dx +\int_0^b g(y)dy \geqq ab \qquad 等号は \quad b=f(a) \quad のとき\]
$これをヤングの不等式といいます。$
$(証明)$
$\hspace{6em} f(a) >b \quad のとき \hspace{15em} f(a) < b \quad のとき$
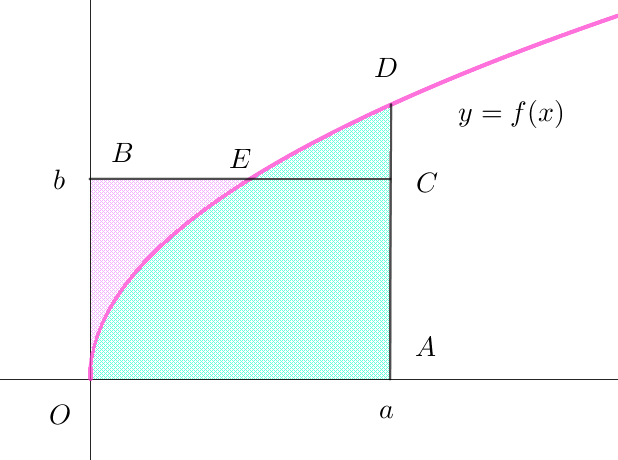
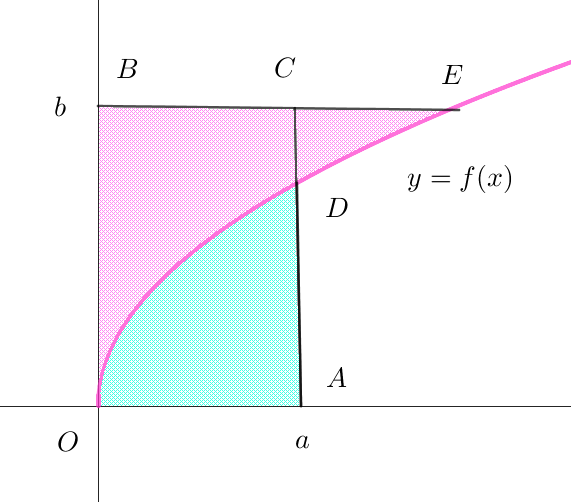
\[上図で、\int _0^a f(x)dx \ \ は水色の部分、\int _0^b g(y)dy \ \ はピンク色の部分の面積を表すからその和は\]
$長方形 \ OACB\ の面積より大きい。$
\[したがって \quad \int _0^a f(x)dx +\int _0^b g(y)dy \geqq ab\]
$等号は \ 3\ 点 \ C,\ D,\ E\ \ で囲まれた領域の面積が \ 0\ のときだから、b=f(a)\ \ (a=g(b)) \ \ のとき$
$上図は、y=f(x)\ が上に凸な場合であるが、下に凸でも同様である。$
メインメニュー に戻る