曲線の凹凸
$下に凸なグラフは、曲線は接線の上側にあるから接線の傾き \ f'(x)\ は、増加する。すなわち \ \ f''(x) > 0$
$上に凸なグラフは、曲線は接線の下側にあるから接線の傾き \ f'(x)\ は、減少する。すなわち \ \ f''(x) < 0$
$\hspace{8em}$

$\hspace{8em}$
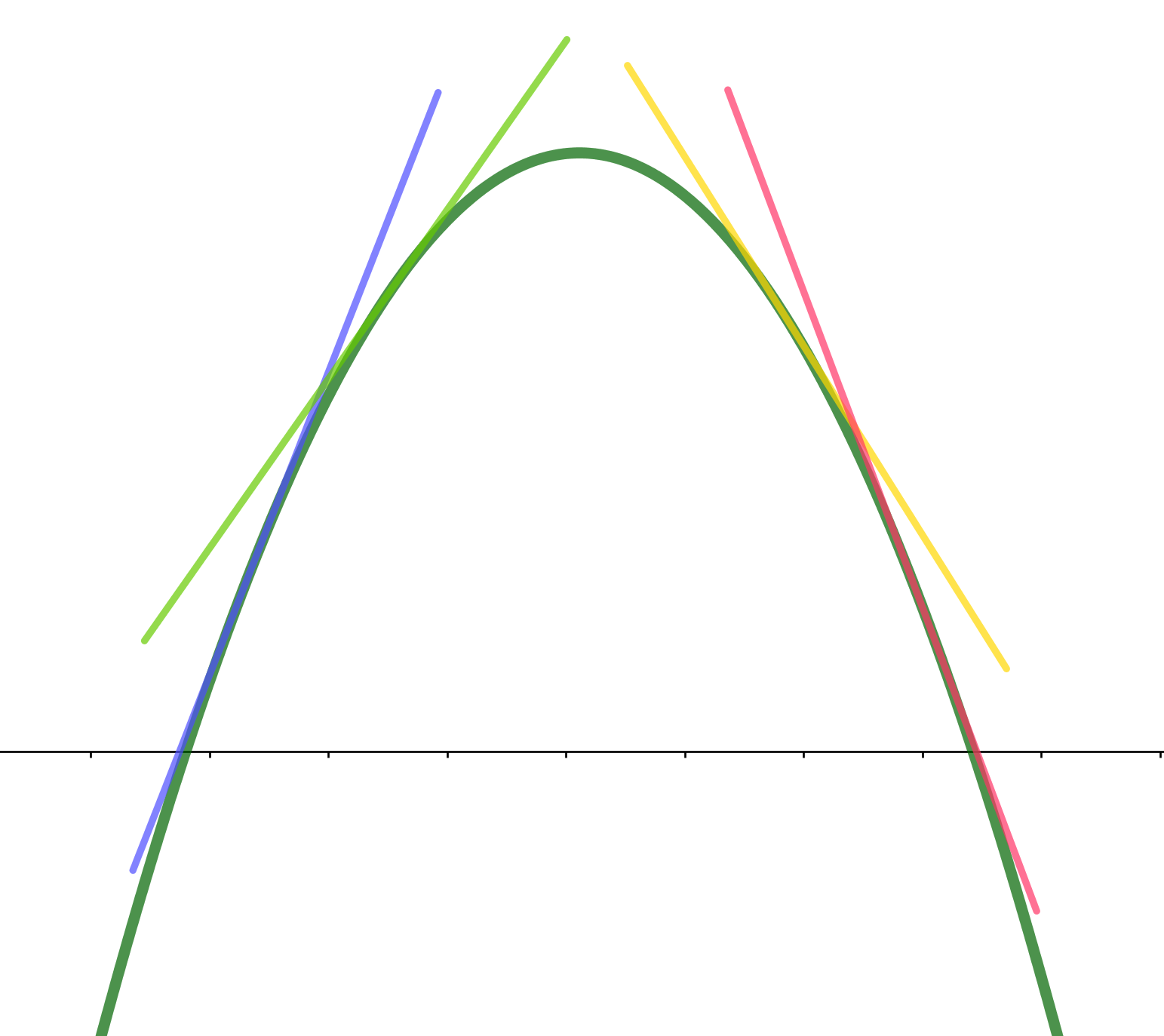
$この程度の記述であり、そもそも曲線が上に凸、下に凸の定義はなく、接線が曲線の上側または下側にある$
$ことの証明もありません。それでも、何となくイメージでわかりますが \cdots $
$それでは、少していねいに考えてみましょう。$
$2\ \ 定義$
$区間 \ [a,\ b]\ で、曲線 \ y=f(x)\ 上の任意の \ 2\ 点 \ A, B\ に対し、$
$\quad (1)\ \ 弦 \ AB\ が弧 \ AB\ の上にあるとき、f(x)\ はこの区間で下に凸$
$\quad (2)\ \ 弦 \ AB\ が弧 \ AB\ の下にあるとき、f(x)\ はこの区間で上に凸$
$という。$
$\hspace{8em}$
$\hspace{8em}$
$次に、この内容を式で表してみましょう。$
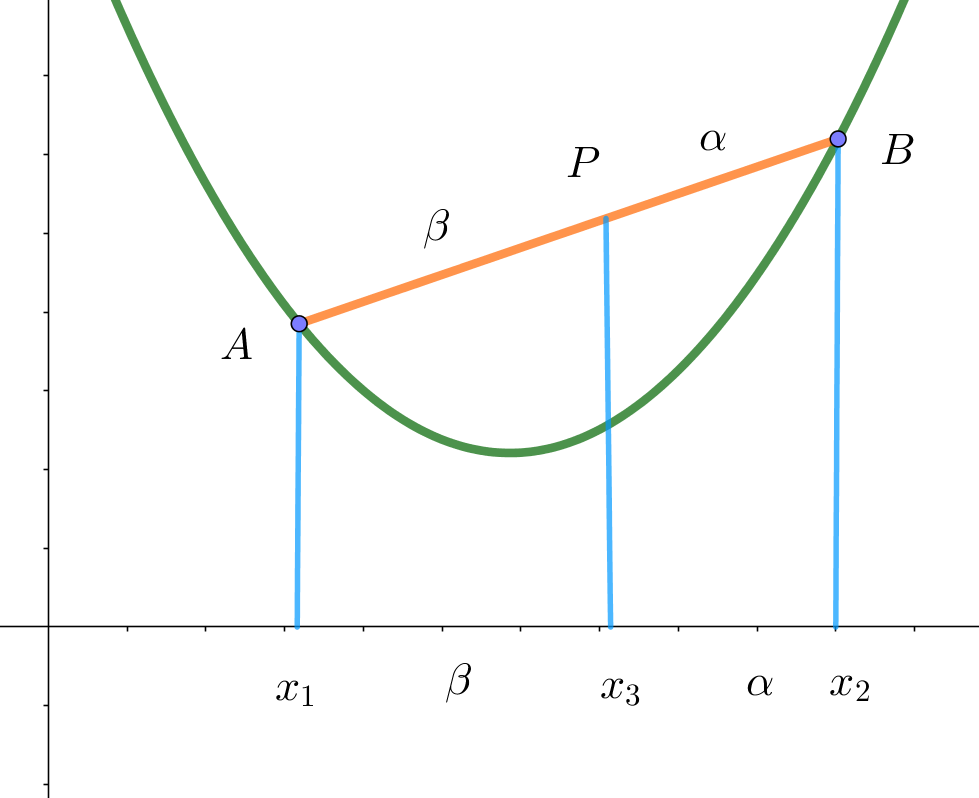
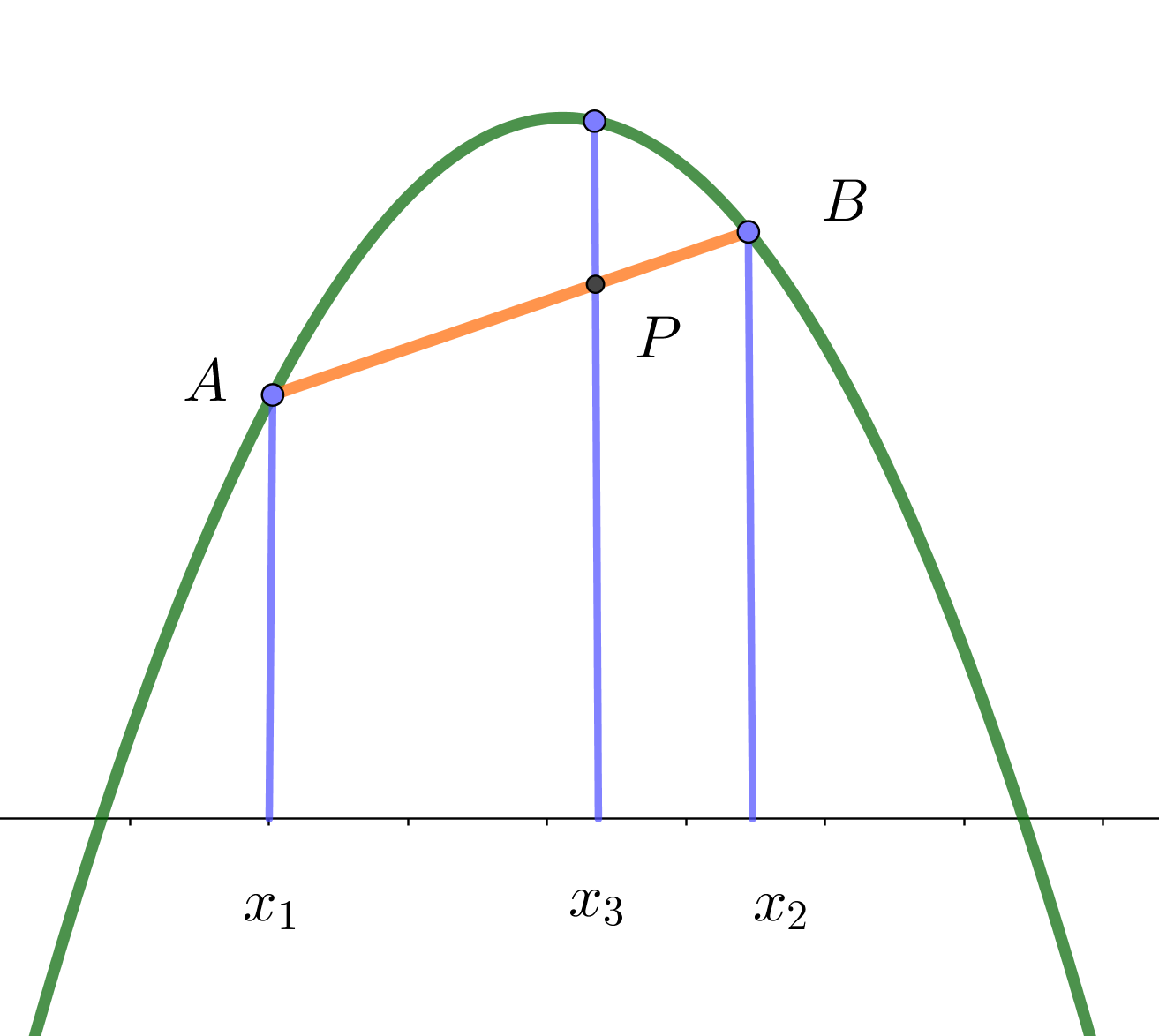
$A(x_1,\ f(x_1)),\ B(x_2,\ f(x_2))\ とし、\alpha > 0,\ \beta > 0,\ \alpha +\beta =1 \ \ とする。$
$線分 \ AB\ を \ \beta : \alpha \ に内分する点 \ P\ の座標 \ (x_3,\ y_3)\ は$
$\qquad x_3=\alpha x_1+\beta x_2 ,\quad y_3=\alpha f(x_1)+\beta f(x_2)$
$したがって$
$\quad (1)\ 下に凸のときは、弦 \ AB\ が弧 \ AB\ の上にあるから、f(\alpha x_1+\beta x_2) \leqq \alpha f(x_1) + \beta f(x_2)$
$\quad (2)\ 上に凸のときは、弦 \ AB\ が弧 \ AB\ の下にあるから、f(\alpha x_1+\beta x_2) \geqq \alpha f(x_1) + \beta f(x_2)$
$3\ \ 定理1$
$関数 \ f(x)\ は区間\ [a, \ b] \ で \ 2\ 回微分可能で、f''(x) \geqq 0 \ \ ならば、f(x)\ はこの区間で下に凸である。$
$この区間内の任意の \ 2\ 数 \ x_1,\ x_2 \ \ (x_1 < x_2) \ について、\alpha > 0,\ \beta > 0 , \alpha + \beta =1 \ \ に対し$
$\quad x_1 < \alpha x_1 +\beta x_2 < x_2 \qquad (差をとって、簡単に証明できる。)$
$平均値の定理より$
$\quad \cfrac{f(\alpha x_1 +\beta x_2)-f(x_1)}{(\alpha x_1+\beta x_2)-x_1}=f'(z_1) \ \ となる \ z_1\ が \ (x_1,\ \alpha x_1+\beta x_2)\ に存在する。$
$(\alpha x_1+\beta x_2)-x_1=\beta x_2-(1-\alpha )x_1=\beta x_2-\beta x_1=\beta (x_2-x_1) \ \ だから$
$\quad f'(z_1)=\cfrac{f(\alpha x_1 +\beta x_2)-f(x_1)}{\beta (x_2-x_1)} \hspace{10em}(1)$
$同様にして$
$\cfrac{f(x_2)-f(\alpha x_1 +\beta x_2)}{x_2-(\alpha x_1+\beta x_2)}=f'(z_2) \ \ となる \ z_2\ が \ (\alpha x_1+\beta x_2,\ x_2)\ に存在する。$
$x_2-(\alpha x_1+\beta x_2)=(1-\beta )x_2-\alpha x_1=\alpha x_2-\alpha x_1=\alpha (x_2-x_1) \ \ だから$
$\quad f'(z_2)=\cfrac{f(x_2)-f(\alpha x_1 +\beta x_2)}{\alpha (x_2-x_1)} \hspace{10em}(2)$
$また、z_1 < z_2 \ \ から f'(z_2)-f'(z_1)=(z_2-z_1)f''(z_3) \ \ となる \ z_3\ が \ (z_1,\ z_2)\ に存在する。$
$\quad z_2-z_1 > 0,\ \ f''(z_3) \geqq 0 \ \ から \quad f'(z_2)-f'(z_1) \geqq 0$
$(1),(2)より$
$\cfrac{f(x_2)-f(\alpha x_1 +\beta x_2)}{\alpha (x_2-x_1)} - \cfrac{f(\alpha x_1+\beta x_2)-f(x_1)}{\beta (x_2-x_1)} \geqq 0$
$分母をはらって$
$\quad \beta \{f(x_2)-f(\alpha x_1 +\beta x_2)\}- \alpha \{f(\alpha x_1+\beta x_2)-f(x_1)\} \geqq 0$
$\quad \alpha f(x_1)+\beta f(x_2) \geqq (\alpha + \beta )f(\alpha x_1 +\beta x_2)$
$\therefore \ \ \alpha f(x_1)+\beta f(x_2) \geqq f(\alpha x_1 +\beta x_2)$
$なお、\alpha ,\ \beta \ のうち一方が \ 0\ のときは、他方が \ 1\ であるから\ \ \alpha f(x_1)+\beta f(x_2) = f(\alpha x_1 +\beta x_2)\ \ が成り立つ$
$以上より、f(x)\ はこの区間で凸関数である。$
$(別証)$
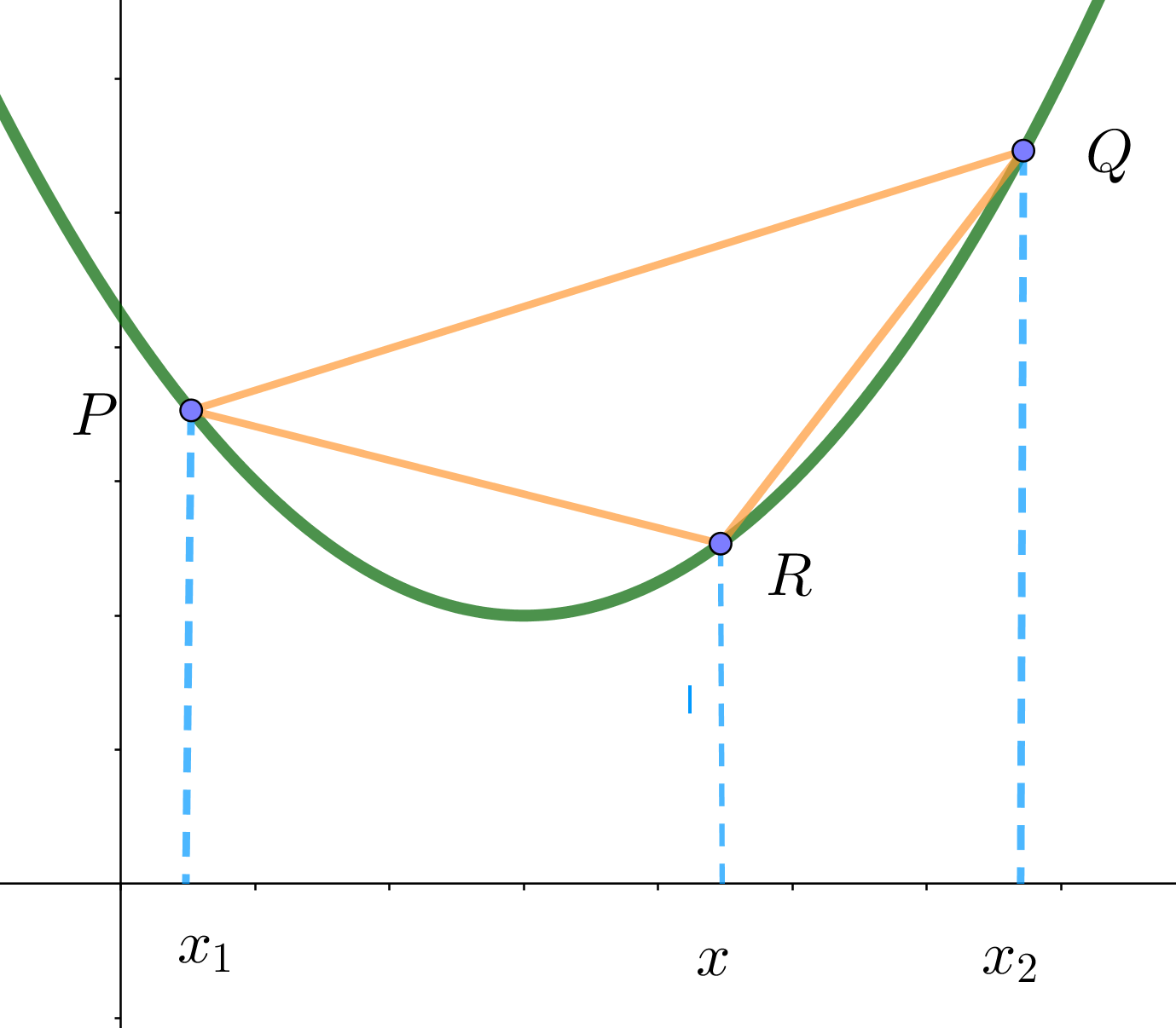
$区間 \ (a,\ b)\ の任意の \ 2\ 数を \ x_1,\ x_2 \ \ (x_1 < x_2)\ とし、$
$曲線上のこの \ 2\ 点を \ P(x_1,\ y_1),\ Q(x_2,\ y_2)\ とする。$
$平均値の定理より$
$\quad \cfrac{y-y_1}{x-x_1}=f'(c_1),\quad \cfrac{y_2-y}{x_2-x}=f'(c_2)$
$を満たす \ c_1,\ c_2\ がそれぞれ \ (x_1,\ x),\ (x,\ x_2)\ に存在する。$
$区間 \ (a,\ b)\ で、f''(x) > 0 \ \ ならば f'(x)\ はこの区間で単調増加だから$
$c_1 < c_2 \ \ より f'(c_1) < f'(c_2)$
$\quad \cfrac{y-y_1}{x-x_1} < \cfrac{y_2-y}{x_2-x} \hspace{10em}(3)$
$分母を払って$
$(x_2-x)(y-y_1) < (x-x_1)(y_2-y)$
$(x_2-x_1+x_1-x)(y-y_1) < (x-x_1)(y_2-y_1+y_1-y)$
$(x_2-x_1)(y-y_1)+(x_1-x)(y-y_1) < (y_2-y_1)(x-x_1)+(x-x_1)(y_1-y)$
$(x_2-x_1)(y-y_1) < (y_2-y_1)(x-x_1)$
$\therefore \ \ y-y_1 < \cfrac{y_2-y_1}{x_2-x_1}(x-x_1)$
$これは、点 \ R(x,\ y)\ が直線 \ PQ\ より下にあることを示しています。$
$すなわち、弧 \ PQ\ が弦 \ PQ\ の下方にあるから \ f(x)\ は下に凸です。$
$f''(x) < 0 \ \ の場合も同様に示される。$
$さらに、f''(x) > 0 \ \ ならば(3)より \ \ (PRの傾き) < (RQの傾き) \ であることもわかる。$
$4 \ \ 定理2\ \ 接線との位置関係$
$曲線 \ y=f(x) \ がある区間で、f''(x) > 0\ \ ならば、この曲線はこの区間の任意の接線の上側にある。$

$曲線上の点 \ P(x,\ f(x))\ における接線 \ PT\ は、$
$\quad y=f'(x_1)(x-x_1)+f(x_1)$
$x_1 < x \ のとき平均値の定理より$
$\quad \cfrac{f(x)-f(x_1)}{x-x_1}=f'(c) \ \ となる \ c\ が \ (x_1,\ x)\ に存在する。$
$f''(x) > 0 \ \ ならば \ f'(x)\ は増加関数だから \quad f'(x_1) < f'(c)$
$\therefore \ \ f'(x_1) < \cfrac{f(x)-f(x_1)}{x-x_1} $
$ f(x) > f'(x_1)(x-x_1)+f(x_1)$
$したがって \quad SQ > SR$
$x < x_1 \ \ のときも同様である。$
メインメニュー に戻る