最速降下曲線

　

$質量mの質点が、xy平面上の2点OとAを結ぶ$
$なめらかな曲線上を重力のみで滑り落ちる$
$とき、かかる時間が最小となる曲線は?$


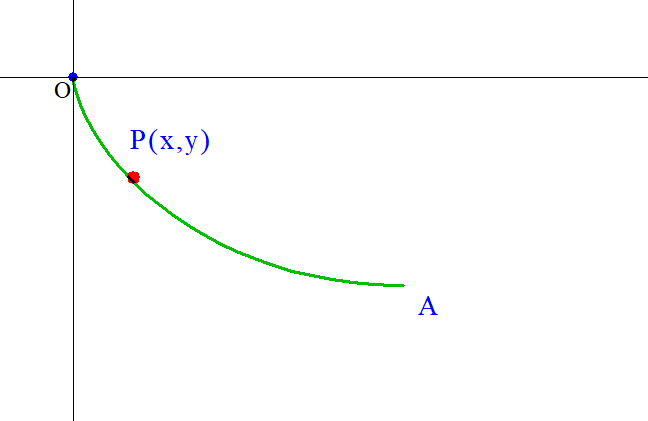
$座標軸を水平方向にx軸、鉛直方向上にy軸$
$の正方向にとる。O(0,0),A(a,b)とする。$
$原点Oでは力学的エネルギーは0であるから$
$点P(x,y)での速度をvとすると$
$\qquad \cfrac{1}{2}mv^2-mgy=0$
$\qquad \therefore v=\sqrt{2gy}$

$曲線に沿った微小の長さ(線素といいます)をds とすると　ds=\sqrt{1+y'^2}dx 　だから$
$かかる時間は$
\[T=\int _0 ^s \cfrac{ds}{v}=\int _0 ^s \cfrac{ds}{\sqrt{2gy}}=\cfrac{1}{\sqrt{2g}}\int _0 ^a \sqrt{\cfrac{1+y'^2}{y}}dx\] $\qquad f=\sqrt{\cfrac{1+y'^2}{y}} 　とおくと$

$\qquad \cfrac{\partial f}{\partial ｘ}=0 , \quad \cfrac{\partial f}{\partial y'}= \cfrac{1}{\sqrt{y}} \cfrac{y'}{\sqrt{1+y'^2}}$

$オイラー・ラグランジュの方程式(2)をつかって　($変分法$を参考にしてください)$

$\qquad \cfrac{d}{dx}\big(f-y'\cfrac{\partial f}{\partial y'}\big) =0 　より　\cfrac{d}{dx}\big(\sqrt{\cfrac{1+y'^2}{y}} -y' \times \cfrac{1}{\sqrt{y}} \cfrac{y'}{\sqrt{1+y'^2}}\big)=0$

$\qquad \sqrt{\cfrac{1+y'^2}{y}} - \cfrac{y'^2}{\sqrt{y}\sqrt{1+y'^2}}=c \quad (cは定数)$

$分母を払ってまとめると$

$\quad (1+y'^2)-y'^2=c\sqrt{y}\sqrt{1+y'^2}$

$\qquad y(1+y'^2)=c \quad (\cfrac{1}{c^2} \rightarrow c と置きかえて)$

$\qquad y'^2=\cfrac{c}{y}-1=\cfrac{c-y}{y}$
$ここで、y=c\sin ^2 \cfrac{t}{2} とおくと　 y'=c\sin \cfrac{t}{2}\cos \cfrac{t}{2} \cfrac{dt}{dx} 　だから$

$\qquad \big(c\sin \cfrac{t}{2}\cos \cfrac{t}{2} \cfrac{dt}{dx}\big)^2=\big(c-c\sin ^2\cfrac{t}{2}\big) \times \cfrac{1}{c\sin ^2\cfrac{t}{2}}=\cfrac{\cos ^2 \cfrac{t}{2}}{c\sin ^2\cfrac{t}{2}}$

$\qquad \therefore c\sin \cfrac{t}{2}\cos \cfrac{t}{2} \cfrac{dt}{dx}=\cfrac{\cos \cfrac{t}{2}}{\sin \cfrac{t}{2}}$

$\qquad \cfrac{dx}{dt}=c\sin ^2 \cfrac{t}{2}=\cfrac{c}{2}(1-\cos t)$
$よって　x=\cfrac{c}{2}(t-\sin t)$
$なお、t=0 \ \ で\ \ x=0 \ \ だから積分定数は0である。$

$もともと、y=c\sin ^2 \cfrac{t}{2} とおいたから　y=\cfrac{c}{2}(1-\cos t)$
$したがって$
\[ \left\{ \begin{array}{l} x=\cfrac{c}{2}(t-\sin t)\\ y=\cfrac{c}{2}(1-\cos t)\\ \end{array} \right. \] $これは、サイクロイド曲線である。$





ページの先頭へ↑



変分法　に戻る


サイクロイド振り子　に戻る


メインメニュー　に戻る