サイクロイド



　
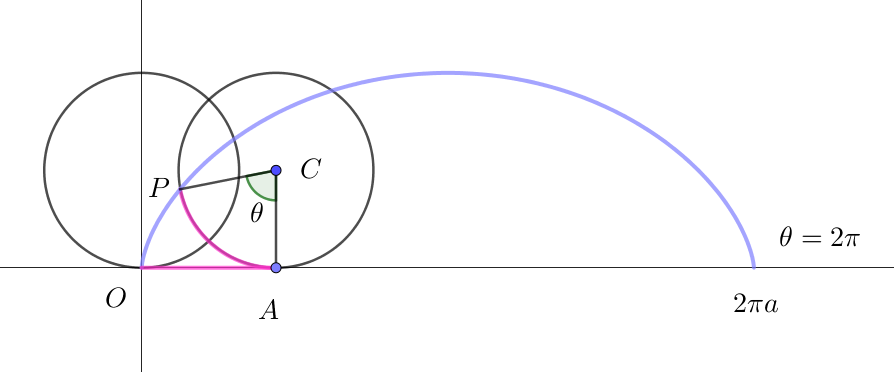
$座標平面上で、半径 \ a\ の円がx軸上を回転する$
$とき円周上の \ 1\ 点の軌跡をサイクロイドと$
$いいます。右図の青色の曲線のことです。$

$始めに原点にあった円周上の点 \ P(x,\ y)\ が$
$x\ 軸の正方向に中心角 \ \theta \ 回転したとき$

$OA=弧PA=a\theta,\quad PB=a\sin \theta,\quad CB=a\cos \theta$

　
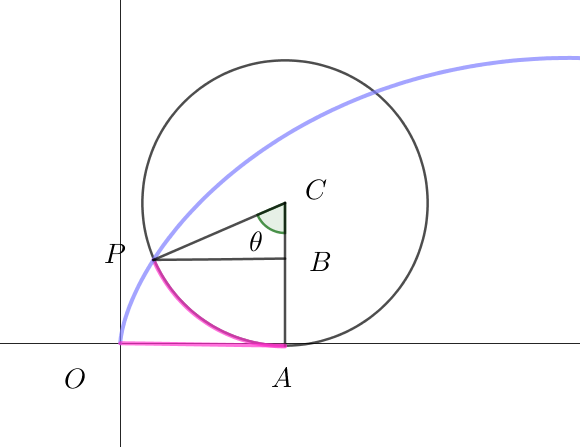
$\quad x=OA-PB=a\theta - a\sin \theta=a(\theta - \sin \theta)$

$\quad y=CA-CB=a - a\cos \theta=a(1- \cos \theta)$

$よって \ \ サイクロイドは$

$\quad x=a(\theta - \sin \theta),\quad y=a(1- \cos \theta)$

$と表される曲線です。$



ページの先頭へ↑




メインメニュー　に戻る