正規分布の確率密度関数
1 測定誤差
$ある量をn回測定したとき、各回の測定値X_1,X_2,\cdots ,X_nは互いに独立な確率変数となります。$
$また、真の値をm(未知)とすると、各回の測定誤差$
$\qquad \varepsilon_1=X_1-m,\ \ \varepsilon_2=X_2-m,\ \ \cdots , \ \ \varepsilon_n=X_n-m $
$は、やはり独立に同じ確率分布にしたがいます。$
$したがって、誤差の同時確率密度関数は独立性から$
$\qquad P(\varepsilon_1,\varepsilon_2,\cdots , \varepsilon_n)=P(\varepsilon_1)P(\varepsilon_2) \cdots P(\varepsilon_n) =P(X_1-m)P(X_2-m) \cdots P(X_n-m) $
$のように、mの関数であらわされます。$
2 誤差分布の確率密度関数
$そこで、あらためて右辺をP(m)とおくと$
$\qquad P(m)=P(X_1-m)P(X_2-m) \cdots P(X_n-m) \hspace{15em}(1)$
$測定値は、真の値mの近くにバラつき、mから遠く離れた値はとらない。(そのような事象の確率は0に近い)$
$したがって、P(m)は$
$\quad m=\overline{X}=\cfrac{X_1+X_2+ \cdots +X_n}{n} \hspace{23em}(2)$
$で最大値をとると考えられます。(この仮定がこの分布を決定づけるものです。)$
$(1)の両辺の対数をとって$
$\qquad \log P(m)=\log P(X_1-m)+\log P(X_2-m)+ \cdots + \log P(X_n-m) $
$両辺をmで微分すると$
$\qquad \cfrac{P'(m)}{P(m)}=\cfrac{P'(X_1-m)}{P(X_1-m)}(-1)+\cfrac{P'(X_2-m)}{P(X_2-m)}(-1)+\cdots +\cfrac{P'(X_n-m)}{P(X_n-m)}(-1)$
$P(m)はm=\overline{X}で最大値をとるから\quad P'(\overline{X})=0$
$よって$
$\qquad \cfrac{P'(X_1-\overline{X})}{P(X_1-\overline{X})}+\cfrac{P'(X_2-\overline{X})}{P(X_2-\overline{X})}+\cdots +\cfrac{P'(X_n-\overline{X})}{P(X_n-\overline{X})}=0$
$ここで、f(X_i-\overline{X})=\cfrac{P'(X_i-\overline{X})}{P(X_i-\overline{X})}\ \ とおくと$
$\qquad f(X_1-\overline{X})+f(X_2-\overline{X})+\cdots + f(X_n-\overline{X})=0 \hspace{15em}(3)$
$また$
$\qquad n \overline{X}=X_1+X_2+ \cdots +X_n \ \ より$
$\qquad (X_1 - \overline{X})+(X_2 - \overline{X})+\cdots +(X_n - \overline{X})=0 \hspace{16em}(4)$
$X_i - \overline{X}をあらためてx_i とおくと$
$(3)は\quad f(x_1)+f(x_2)+\cdots +f(x_n)=0$
$(4)は\quad x_1+x_2+\cdots +x_n=0$
$これらを満たす関数f(x)はf(x)=ax\ \ (aは定数)です。($ コーシーの関数方程式$参照)\ $
$x \rightarrow x-m \ \ とおいて、f(x - m)=a(x -m)$
$\qquad \cfrac{P'(x-m)}{P(x-m)}=a(x-m)$
$積分して$
$\qquad \log P(x-m)=\cfrac{a}{2}(x-m)^2+C$
$\qquad P(x-m)=Ce^{\dfrac{a}{2}(x-m)^2}$
$右辺をあらためてP(x)とおくと$
$\qquad P(x)=Ce^{\dfrac{a}{2}(x-m)^2}$
$x \rightarrow \pm \infty \ \ のとき \ \ P(x) \rightarrow 0 \ \ (誤差の考え)だから \ \ a <0$
$あらためて、 a \ を -a \ \ (a >0)とおいて$
$\qquad P(x)=Ce^{-\dfrac{a}{2}(x-m)^2}$
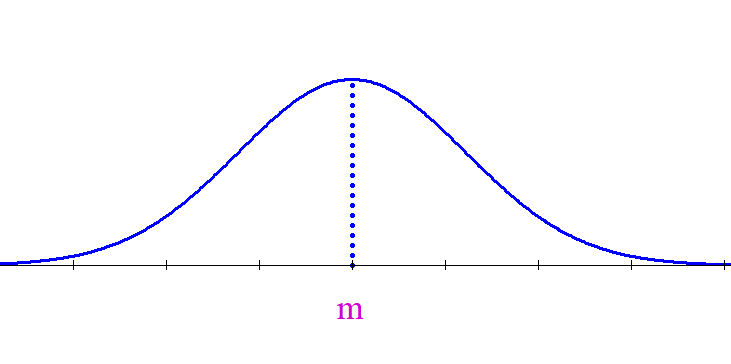
$これが、(1)\ \ すなわち誤差分布の確率密度関数です。$
$グラフは右図のとおりです。$
3 正規分布
$誤差分布の確率密度関数のCとaを決定しましょう。$
(i)$\ \ P(x) \geqq 0 \ \ だから C > 0$
(ii)$\ \ $ \[ 全確率 \ 1\ \ より \quad \int_{-\infty} ^\infty f(x)dx = 1 \quad \therefore C \int_{-\infty}^\infty e^{-\cfrac{a}{2}(x-m)^2}dx = 1 \]
$この積分をIとし、\sqrt{\dfrac{a}{2}}(x-m)=t \ \ とおくと \sqrt{\dfrac{a}{2}}dx =dt $
\[I=C \sqrt{\dfrac{2}{a}} \int_{-\infty}^\infty e^{-t^2}dt \] $この積分はガウス積分だから($ ガウス積分$参照)$
$\qquad I=C \sqrt{\dfrac{2}{a}} \sqrt{\pi}$
$\qquad \therefore C \sqrt{\dfrac{2}{a}} \sqrt{\pi}=1 \ \ より C=\sqrt{\dfrac{a}{2\pi}}$
(iii)$\ \ 平均$
\begin{eqnarray*} E &=& \int_{-\infty} ^\infty xf(x)dx \\ &=&C \int_{-\infty}^\infty x e^{-\dfrac{a}{2}(x-m)^2}dx \\ \end{eqnarray*} $\sqrt{\dfrac{a}{2}}(x-m)=t \ \ とおくと \sqrt{\dfrac{a}{2}}dx =dt ,\quad x=m+\sqrt{\dfrac{2}{a}}\ t$
\begin{eqnarray*} E &=&C \int_{-\infty}^\infty (m+\sqrt{\dfrac{2}{a}}t) e^{-t^2} \sqrt{\dfrac{2}{a}} dt \\ \\ &=&C \sqrt{\dfrac{2}{a}} \int_{-\infty}^\infty (m+\sqrt{\dfrac{2}{a}}\ t) e^{-t^2} dt \\ \\ &=&mC \sqrt{\dfrac{2}{a}} \underbrace{\int_{-\infty}^\infty e^{-t^2} dt}_{\substack{ガウス積分}} + C\ \cfrac{2}{a} \underbrace{\int_{-\infty}^\infty t e^{-t^2} dt}_{\substack{奇関数だから0}} \\ \\ &=&mC \sqrt{\dfrac{2}{a}} \times \sqrt{\pi}\\ \\ &=&m \times \sqrt{\dfrac{a}{2\pi}} \times \sqrt{\dfrac{2}{a}} \times \sqrt{\pi}\\ \\ &=&m\\ \end{eqnarray*}
(iv)$\ \ 分散$
\begin{eqnarray*} V &=& \int_{-\infty} ^\infty (x-m)^2f(x)dx \\ \\ &=&C\int_{-\infty}^\infty (x-m)^2 e^{-\dfrac{a}{2}(x-m)^2}dx \\ \end{eqnarray*} $\sqrt{\dfrac{a}{2}}(x-m)=t \ \ とおくと \sqrt{\dfrac{a}{2}}dx =dt ,\quad x-m=\sqrt{\dfrac{2}{a}}\ t$
\begin{eqnarray*} V &=&C \int_{-\infty}^\infty \cfrac{2}{a}\ t^2 \ e^{-t^2} \sqrt{\dfrac{2}{a}} dt \\ \\ &=&C \ \cfrac{2}{a}\sqrt{\dfrac{2}{a}} \int_{-\infty}^\infty t^2 e^{-t^2} dt \\ \end{eqnarray*} \begin{eqnarray*} I &=&\int_{-\infty}^\infty t^2 e^{-t^2} dt \\ \\ &=&-\cfrac{1}{2}\int_{-\infty}^\infty t (-2t)e^{-t^2} dt \\ \\ &=&-\cfrac{1}{2}\underbrace{\big[t e^{-t^2} \big]_{-\infty}^\infty }_{\substack{=0}}+\cfrac{1}{2}\int_{-\infty}^\infty e^{-t^2} dt \\ \\ &=&\cfrac{1}{2}\int_{-\infty}^\infty e^{-t^2} dt \\ \\ &=&\cfrac{\sqrt{\pi}}{2}\\ \end{eqnarray*}
$よって、V=\sqrt{\dfrac{a}{2\pi}} \times \cfrac{2}{a}\sqrt{\dfrac{2}{a}} \times \cfrac{\sqrt{\pi}}{2}=\cfrac{1}{a}$
$分散を \sigma ^2 とおくと \quad a=\cfrac{1}{\sigma ^2} \ \ より C=\cfrac{1}{\sqrt{2\pi}\sigma}$
$よって、f(x)=\cfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{1}{2\sigma ^2}(x-m)^2}$
$この、平均m,標準偏差\sigma の確率密度関数を正規分布といい、N(m,\sigma ^2) とあらわします。$
$ほとんどの統計学の本の記述は、「このような確率密度関数をもつ分布を正規分布という」となっていますが、$
$上のような内容が省略されているわけです。$
$正規分布を初めて導いたのはガウスですが、ガウスがどのように考えたのかは不勉強でわかりません。$
メインメニュー に戻る