MY MATH NOTE

平面極座標への変数変換

$関数 \ f(x,\ y)\ に対して、x\ y\ 平面での領域 \ D\ 内の点と \ x=r\cos \theta,\ y=r\sin \theta \ \ (r > 0,\ \ 0 \leqq \theta < 2\pi)$
$と変数変換した極座標平面で表された領域 \ E\ 内の点が \ 1\ 対 \ 1\ に対応するとき$
\[\qquad \iint_D f(x,y)dxdy=\iint_{E}f(r\cos \theta,r\sin \theta)rdrd\theta\]

　
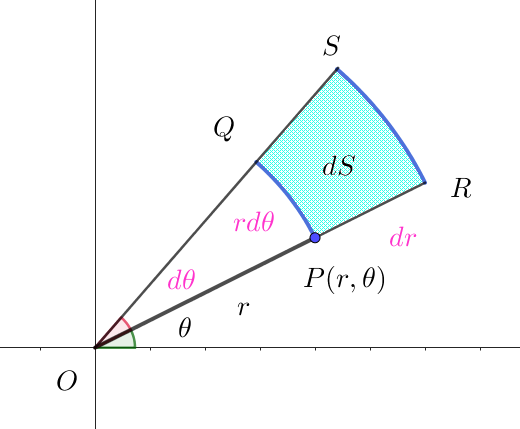
$関数 \ f(x,\ y)\ の \ x\ y\ 平面での積分領域 \ D\ 内の点 \ (x,\ y)\ の極座標での対応点を$

$P(r,\ \theta)\ とし、Q(r,\ \theta+d\theta),\ \ R(r+dr,\ \theta),\ \ S(r+dr,\ \theta +d\theta)\ \ とおくと、$

$微小領域 \ PRSQ\ は微小長方形と見なせる。$

$線分 \ PR=dr,\ 弧 \ PQ=rd\theta \ \ だから\ \ この微小領域 \ PRSQ\ の面積は$

$\quad dS \fallingdotseq PR \times PQ=dr \times rd\theta=rdrd\theta$


$(証明2)$

$証明1の図で$
\begin{eqnarray*} dS &=&扇形ORS - 扇形OPQ\\ \\ &=&\cfrac{1}{2}(r+dr)^2 d \theta -\cfrac{1}{2}r^2 d \theta\\ \\ &=&\cfrac{1}{2}(2rdr+dr^2)d \theta \qquad (2次の項を無視して)\\ \\ &=&rdr d \theta\\ \end{eqnarray*}

$ベクトル解析の考え方($球面座標によるラプラシアン$)をご覧ください)をつかって、$
$もう少し数学的に証明しましょう。$

$(証明3)$

$\boldsymbol r=(r\cos \theta , \ r\sin \theta) \ \ とおくと$

$r\ 曲線と \ \theta \ 曲線の接線ベクトルは \quad \cfrac{\partial \boldsymbol r}{\partial r}=(\cos \theta ,\ \sin \theta ),\quad \cfrac{\partial \boldsymbol r}{\partial \theta}=(-r\sin \theta ,\ r\cos \theta ) \quad より$

$\cfrac{\partial \boldsymbol r}{\partial r} \cdot \cfrac{\partial \boldsymbol r}{\partial \theta}=\cos \theta \times (-r\sin \theta )+ \sin \theta \times r\cos \theta =0 \quad \therefore \ \ \cfrac{\partial \boldsymbol r}{\partial r} \perp \cfrac{\partial \boldsymbol r}{\partial \theta}$

　
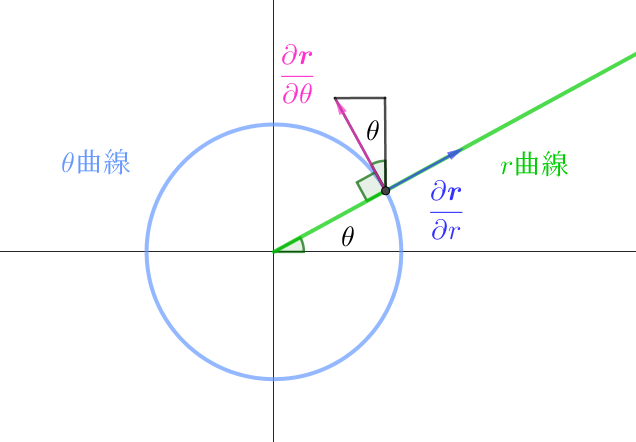
$r\ 曲線の線素(弧長) \ \ ds_1 \ \ は \ \theta \ が一定だから$
\begin{eqnarray*} ds_1 ^2 &=&dx ^2+dy ^2\\ \\ &=&\big(\cfrac{\partial x}{\partial r}dr \big)^2+\big(\cfrac{\partial y}{\partial r}dr \big)^2\\ \\ &=&\big \{\big(\cfrac{\partial x}{\partial r}\big)^2+\big(\cfrac{\partial y}{\partial r} \big)^2 \big \}dr ^2\\ \\ &=&(\cos ^2 \theta +\sin ^2\theta) dr^2\\ \\ &=&dr^2\\ \end{eqnarray*} $\therefore \ \ ds_1=dr$

$\theta \ 曲線の線素(弧長) \ \ ds_2 \ \ は \ r\ が一定だから$
\begin{eqnarray*} ds_2 ^2 &=&dx ^2+dy ^2\\ \\ &=&\big(\cfrac{\partial x}{\partial \theta}d\theta \big)^2+\big(\cfrac{\partial y}{\partial \theta}d\theta \big)^2\\ \\ &=&\big \{\big(\cfrac{\partial x}{\partial \theta}\big)^2+\big(\cfrac{\partial y}{\partial \theta} \big)^2 \big \}d \theta ^2\\ \\ &=&((-r\sin \theta)^2 +(r\cos \theta)^2) d \theta^2\\ \\ &=&r^2d \theta ^2\\ \end{eqnarray*} $\therefore \ \ ds_2=rd \theta$

$よって \quad 点 \ P(r,\ \theta)\ \ における微小領域の面積 \ dS\ は$

$\quad dS \fallingdotseq ds_1 \times ds_2=dr \times rd\theta=rdrd\theta$


$なお、応用問題は($その3 2重積分の極座標変換$)をご覧ください。$

　

ページの先頭へ↑