平面におけるグリーンの定理
$xy\ 平面上で、閉曲線 \ C\ が自分自身と交わらないとき、単一閉曲線といい、C\ の内部を左にみる回転を正とします。$
$2\ 重積分と$線積分$の間には次の定理が成りたちます。$
1 平面におけるグリーンの定理
$単一閉曲線 \ C\ で囲まれた領域を \ D\ とし、D\ で連続な偏導関数をもつ \ 2\ つの関数を \ P(x,\ y),\ Q(x,\ y)\ とすると$
\[\iint _D \big(\cfrac{\partial P}{\partial x}- \cfrac{\partial Q}{\partial y}\big)dx dy=\oint _C(Qdx+Pdy) \]
$これを平面におけるグリーンの定理といいます。$
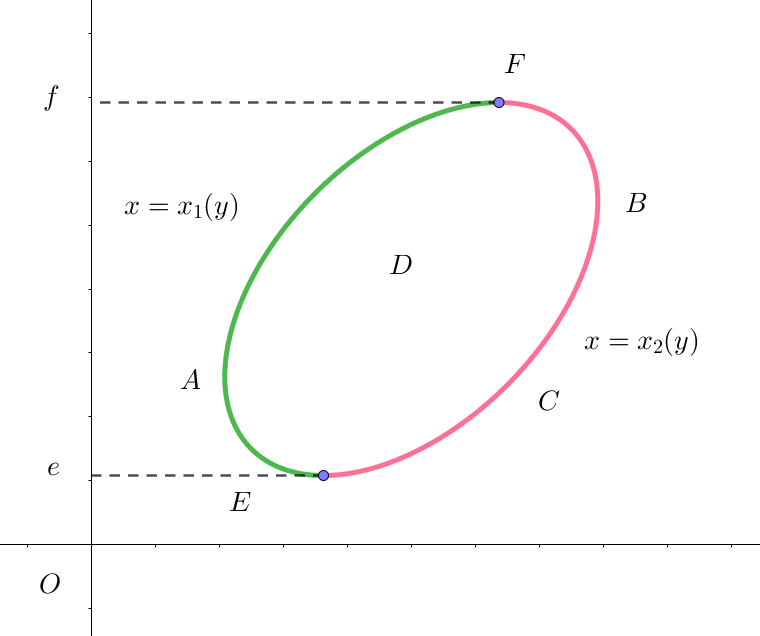
$右図のように、方程式 \ x=x_2(y)\ で表される曲線 \ EBF \ と方程式 \ x=x_1(y)\ で表される曲線 \ FAE\ で囲まれた$
$単一閉曲線 \ C\ を考えます。$
$曲線 \ C\ は、e \leqq y \leqq f ,\qquad x_1(y) \leqq x_2(y) \quad がなりたちます。$
$(1)\ \ 左辺の第 \ 1\ 項$
\begin{eqnarray*}
& &\iint _D \cfrac{\partial P}{\partial x}dx dy\\
\\
&=&\int _e^f\int _{x_1(y)}^{x_2(y)}\cfrac{\partial P}{\partial x}dx dy\\
\\
&=&\int _e^f\big[P(x,y)\big] _{x_1(y)}^{x_2(y)}\ dy\\
\\
&=&\int _e^f\big(P(x_2(y),y)-P(x_1(y),y)\big)dy\\
\\
&=&\int _e^f P(x_2(y),y)dy + \int _f^e P(x_1(y),y)dy\\
\\
&=&\oint _C P dy\\
\end{eqnarray*}
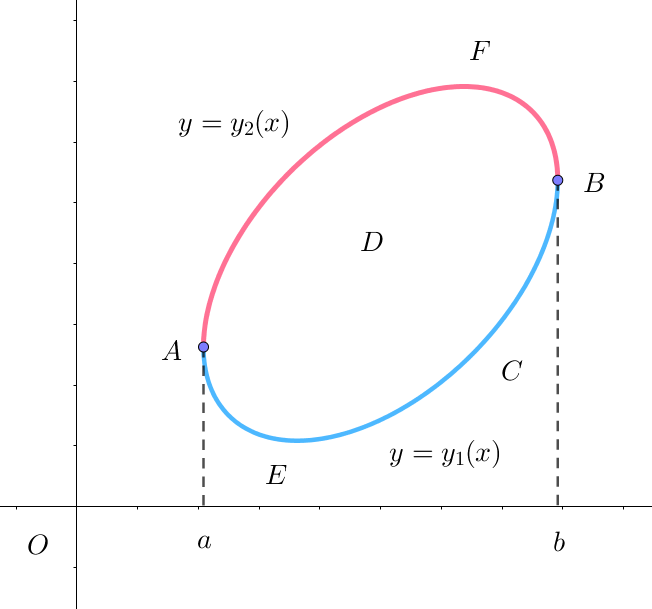
$同様にして、方程式 \ y=y_1(x)\ で表される曲線 \ AEB \ と方程式 \ y=y_2(x)\ で表される曲線 \ BFA\ で囲まれた$
$単一閉曲線を考えます。$
$曲線 \ C\ は、a \leqq x \leqq b ,\qquad y_1(x) \leqq y_2(x) \quad がなりたちます。$
$(2)\ \ 左辺の第 \ 2\ 項$
\begin{eqnarray*}
& &-\iint _D \cfrac{\partial Q}{\partial y}dx dy\\
\\
&=&-\int _a^b\int _{y_1(x)}^{y_2(x)}\cfrac{\partial Q}{\partial y}dy dx\\
\\
&=&-\int _a^b\big[Q(x,y)\big] _{y_1(x)}^{y_2(x)}dx\\
\\
&=&-\int _a^b\big(Q(x,y_2(x))-P(x,y_1(x))\big)dx\\
\\
&=&\int _b^a Q(x,y_2(x))dx + \int _a^b P(x,y_1(x))dx\\
\\
&=&\oint _C Q dx\\
\end{eqnarray*}
$(1),(2)より定理が成りたつ。$
2 閉曲線で囲まれた領域の面積
$単一閉曲線 \ C\ で囲まれた領域 \ D\ の面積 \ S\ は$
\[S=\oint _C xdy=-\oint _C ydx=\cfrac{1}{2}(xdy-ydx) \]
$グリーンの定理で$
\[P=x,\quad Q=0 \quad とおくと \quad \iint_D dxdy=\oint_C xdy \quad より \quad S=\oint _C xdy\] $\hspace{4em} (これは高校の積分で学習する公式です。)$
\[P=0,\quad Q=y \quad とおくと \quad -\iint_D dxdy=\oint_C ydx \quad より \quad S=-\oint _C ydx\] \[この \ 2\ 式を加えると \quad 2S=\oint _C(xdy-ydx)\]
$例1$
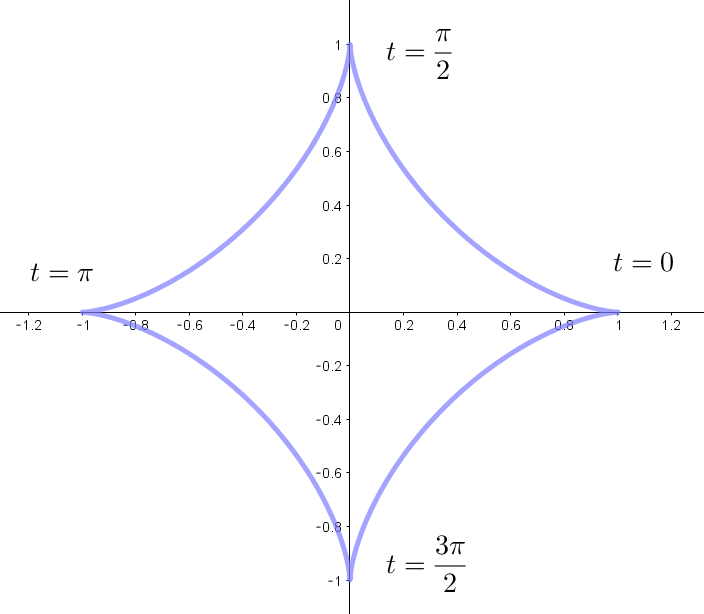
$閉曲線 \ \ x=a\cos ^3t,y=a\sin ^3t \quad (a >0,\ \ 0 \leqq t \leqq 2\pi)\ \ で囲まれた図形の面積$
$この閉曲線はアステロイドと呼ばれていますが、右図は \ a=1 \ のグラフです。$
\begin{eqnarray*}
& &xdy-ydx\\
\\
&=&(a\cos ^3 t\cdot 3a\sin ^2 t \cos t - a\sin ^3 t \cdot 3a\cos ^2 t(-\sin t))dt\\
\\
&=&3a^2\sin ^2 t\cos ^2 t(\sin ^2 t + \cos ^2 t)dt\\
\\
&=&3a^2\sin ^2 t\cos ^2 t dt\\
\\
&=&\cfrac{3}{4}a^2\sin ^22t dt\\
\\
&=&\cfrac{3}{8}a^2(1-\cos 4t) dt\\
\end{eqnarray*}
$したがって$
\begin{eqnarray*}
S
&=&\cfrac{1}{2}\int _0^{2\pi} \cfrac{3}{8}a^2(1-\cos 4t)dt\\
\\
&=&\cfrac{3}{16}a^2 \big [t-\cfrac{1}{4}\sin 4t\big ] _0^{2\pi}\\
\\
&=&\cfrac{3}{16}a^2 \times 2\pi \\
\\
&=&\cfrac{3}{8}\pi a^2
\end{eqnarray*}
$別解として、高校の数学で求めて見ましょう$
\begin{eqnarray*}
S
&=&4\int _{\scriptsize{\cfrac{\pi}{2}}}^0 ydx\\
\\
&=&4\int _{\scriptsize{\cfrac{\pi}{2}}}^0 y\cfrac{dx}{dt}dt\\
\\
&=&4\int _{\scriptsize{\cfrac{\pi}{2}}}^0 a\sin ^3 t \cdot 3a\cos ^2 t(-\sin t)dt\\
\\
&=&12a^2\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 t \cos ^2 tdt\\
\\
&=&12a^2\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 t (1-\sin ^2 t)dt\\
\\
&=&12a^2\big(\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^4 tdt - \int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^6 tdt \big)\\
\\
&=&12a^2\big(\cfrac{3}{4} \times \cfrac{1}{2} \times \cfrac{\pi}{2}-\cfrac{5}{6} \times \cfrac{3}{4} \times \cfrac{1}{2} \times \cfrac{\pi}{2}\big)\\
\\
&=&\cfrac{3}{8}\pi a^2
\end{eqnarray*}
\[\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^n tdt \quad については\]
$\hspace{5em}$ 正弦と余弦の累乗の定積分$\ \ を参考にしてください。$
メインメニュー に戻る