線積分
$平面でも空間でも内容は同じですので、空間で説明します。$
1 媒介変数tに関する線積分
$曲線 \ C\ が \ t\ を媒介変数として x=x(t),\ \ y=y(t),\ \ z=z(t)\ \ (a \leqq t \leqq b)\ \ と表されるとき$
$C\ 上の連続なスカラー関数を \ \ \phi(x,\ y,\ z)\ \ とする。$
$区間 \ [a,\ b]\ を分割して \quad \Delta :a=t_0,\ t_1,\ t_2,\ \cdots ,\ t_{n-1},\ t_n=b \ \ とし、各小区間 \ [t_{i-1},\ t_i]\ に任意に \ \xi_i \ をとり$
$n \longrightarrow \infty \quad として、分割 \ \ \Delta \ を細かくして各小区間 \ [t_{i-1},\ t_i]\ の長さを限りなく \ 0\ にしたとき、$
\[\sum _{i=1}^n \phi(x(\xi_i),\ y(\xi_i),\ z(\xi_i))(x(\xi_i)-x(\xi_{i-1}))\] $が極限値をもつならば、これを曲線 \ C\ に沿うスカラー関数 \ \phi(x,\ y,\ z)\ の \ t\ に関する線積分といい$
\[\int _C \phi(x,y,z)dx=\int _C \phi(x,y,z)\cfrac{dx}{dt}dt \quad とあらわす\] \[\int _C \phi(x,y,z)dy ,\qquad \int _C \phi(x,y,z)dz \quad も同様です。\]
\[とくに、曲線 \ C\ が閉曲線のときは、\oint \ \ という積分記号がつかわれます。\]
$例1$
\[曲線 \ C :x^2+y^2=r^2 \quad として \quad \oint _C xdy \quad を求めてみましょう。\] $\quad C\ を \ \ x=r\cos t ,\quad y=r\sin t \quad (r>0,\quad 0 \leqq t \leqq 2\pi)\ と媒介変数表示すると$
\begin{eqnarray*} \oint _C xdy &=&\int _0^{2\pi}r\cos t \cdot r\cos tdt\\ \\ &=&\cfrac{r^2}{2}\int _0^{2\pi}(1+\cos 2t)dt\\ \\ &=&\cfrac{r^2}{2}\big[t+\cfrac{1}{2}\sin 2t\big] _0^{2\pi}\\ \\ &=&\pi r^2 \end{eqnarray*} $この積分がなぜ \ C\ の囲む円の面積に等しいかは$平面におけるグリーンの定理$をご覧ください。$
$例2$
$\quad スカラー場 \quad \phi(x,\ y,\ z)=x+y+z \quad について、原点と点\ A(2,\ 1,\ 3)を結ぶ線分を \ C\ とするとき$
\[\int _C \phi(x,y,z)dx \quad を求めてみましょう。\]
$\quad 直線 \ OA\ のベクトル方程式は \quad \vec{OA}=t\vec{OA} =(2t,\ t,\ 3t) \qquad (0 \leqq t \leqq 1) \quad だから$
$\quad 線分 \ C\ の媒介変数表示は \quad x(t)=2t,\ \ y(t)=t,\ \ z(t)=3t $
$\quad このとき \quad \phi(x,\ y,\ z)=2t+t+3t=6t \qquad dx=2dt$
\[\therefore \ \ \int _C \phi(x,y,z)dx =\int _0^1 6t \cdot 2dt=6\]
2 弧長に関する線積分
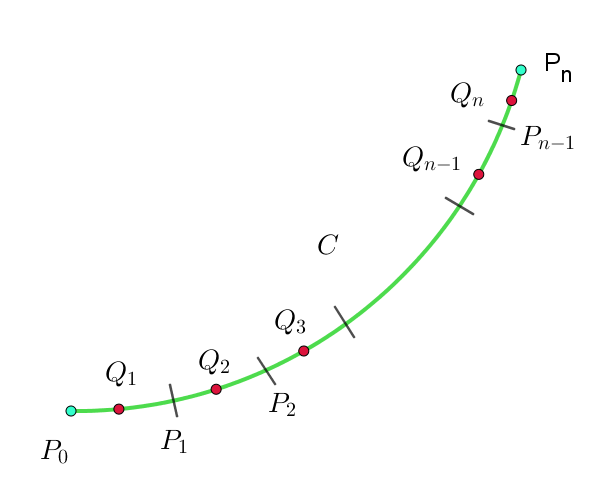
$2\ 点 \ P,\ Q\ を両端とする曲線 \ C\ が \ t\ を媒介変数として x=x(t),\ \ y=y(t),\ \ z=z(t)$
$と表されるとき、C\ 上の連続なスカラー関数を \ \ \phi(x,\ y,\ z)\ \ とする。$
$曲線 \ C\ を \ P_1,\ P_2,\ \cdots \ P_{n-1}\ で \ n\ 個の微小部分に分割し、P_0=P,\ P_n=Q \ とする。$
$それぞれの微小部分の弧の長さを \quad P_0P_1=\Delta s_1,\ \ P_1P_2=\Delta s_2,\ \cdots ,\ P_{n-1}P_n=\Delta s_n $
$とし、これらの各弧上に任意に\ 点 \ Q_1,\ \ Q_2,\ \cdots,\ Q_n \ \ をとる。$
$\qquad n \longrightarrow \infty \quad として、分割を細かくして各微小部分の長さ \ \Delta s_i \ \ (i=1,\ 2,\ \cdots , \ n)を限りなく \ 0\ にしたとき$
\[\sum _{i=1}^n \phi(Q_i)\Delta s_i \quad が極限値をもつならば、これを曲線 \ C\ に沿うスカラー関数 \ \phi(x,\ y,\ z)\ の\]
\[弧長に関する線積分といい \quad \int _C \phi(x,y,z)ds \quad とあらわす。\]
$\qquad \cfrac{ds}{dt}=\sqrt{\big(\cfrac{dx}{dt}\big)^2+\big(\cfrac{dy}{dt}\big)^2+\big(\cfrac{dz}{dt}\big)^2} \quad だから$
\[\int _C \phi(x,y,z)ds =\int _C \phi(x(t),y(t),z(t))\sqrt{\big(\cfrac{dx}{dt}\big)^2+\big(\cfrac{dy}{dt}\big)^2+\big(\cfrac{dz}{dt}\big)^2} dt\]
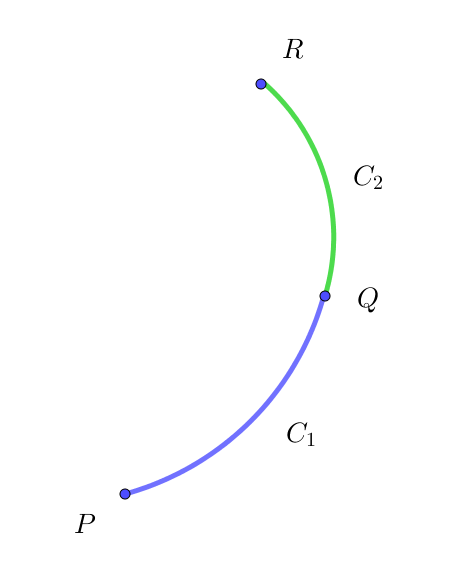
$また、右図のように曲線 \ C\ が分割されているときは$
$ \ \ C_1\ :\ PQ\ 間、C_2\ :\ QR\ 間に分ければよい。$
\[\int _C \phi(x,y,z)ds =\int _{C_1} \phi(x,y,z)ds + \int _{C_2} \phi(x,y,z)ds \]
$例3$
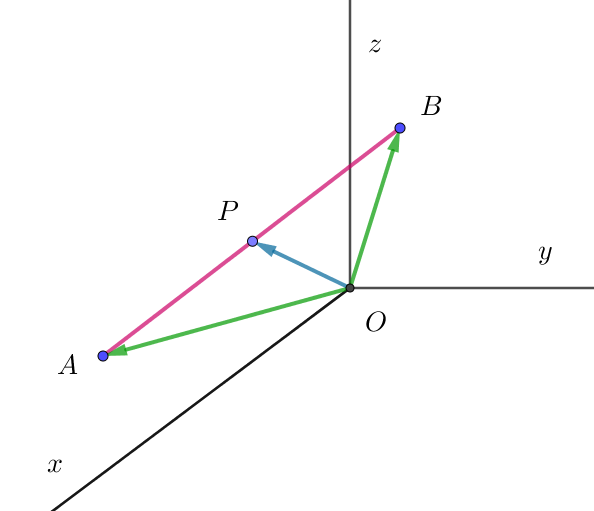
$スカラー場 \quad \phi=x^2+y^2+z^2 \quad について、点 \ A(1,\ -1,\ 0),\ \ B(2,\ 1,\ 2)\ \ とする。$
$(1)\quad 線分 \ AB\ に沿った線積分$
$\quad 直線 \ AB\ のベクトル方程式は$
\begin{eqnarray*}
\vec{OP}
&=&\vec{OA}+t\vec{AB} \qquad (0 \leqq t \leqq 1)\\
\\
&=&(1,\ -1,\ 0)+t(1,\ 2,\ 2)\\
\\
&=&(t+1,\ 2t-1,\ 2t)
\end{eqnarray*}
$\quad 線分 \ AB\ の媒介変数表示は \quad x(t)=t+1,\ \ y(t)=2t-1,\ \ z(t)=2t $
$\quad このとき \quad \phi=(t+1)^2+(2t-1)^2+(2t)^2=9t^2-2t+2$
$\quad \cfrac{ds}{dt}=\sqrt{\big(\cfrac{dx}{dt}\big)^2+\big(\cfrac{dy}{dt}\big)^2+\big(\cfrac{dz}{dt}\big)^2}=\sqrt{1^2+2^2+2^2}=3$
\[\therefore \ \ \int _C \phi(x,y,z)ds =\int _0^1(9t^2-2t+2) \cdot 3dt=12\]
$(2)\quad 折れ線 \ AOB\ に沿った線積分$
(i)$\ \ 線分 \ AO\ 上では$
$\quad 直線 \ AO\ のベクトル方程式は$
\begin{eqnarray*}
\vec{AO}
&=&\vec{OA}+t\vec{AO} \qquad (0 \leqq t \leqq 1)\\
\\
&=&(1,\ -1,\ 0) + t(-1,\ 1,\ 0)\\
\\
&=&(-t+1,\ t-1,\ 0)
\end{eqnarray*}
$\quad よって \ 線分 \ AO\ の媒介変数表示は \quad x(t)=-t+1,\ \ y(t)=t-1,\ \ z(t)=0 $
$\quad このとき \quad \phi=(-t+1)^2+(t-1)^2=2t^2-4t+2 \qquad \cfrac{ds}{dt}=\sqrt{(-1)^2+1^2}=\sqrt{2}$
\[\therefore \ \ \int _{AO} \phi(x,y,z)ds =\int _0^1(2t^2-4t+2) \cdot \sqrt{2}dt=\cfrac{2\sqrt{2}}{3}\]
(ii)$\ \ 線分 \ OB\ 上では$
$\quad 直線 \ OB\ のベクトル方程式は$
$\qquad \vec{OB}=t\vec{OB}=(2t,\ t,\ 2t) \qquad (0 \leqq t \leqq 1)$
$\quad よって \ 線分 \ OB\ の媒介変数表示は \quad x(t)=2t,\ \ y(t)=t,\ \ z(t)=2t $
$\quad このとき \quad \phi=(2t)^2+t^2+(2t)^2=9t^2 \qquad \cfrac{ds}{dt}=\sqrt{2^2+1^2+2^2}=3$
\[\therefore \ \ \int _{OB} \phi(x,y,z)ds =\int _0^1 9t^2 \cdot 3dt=9\]
(i),(ii)$\ \ より$
\[\int _C \phi(x,y,z)ds =\int _{AO} \phi(x,y,z)ds + \int _{OB} \phi(x,y,z)ds= \cfrac{2\sqrt{2}}{3}+9\]
$例4$
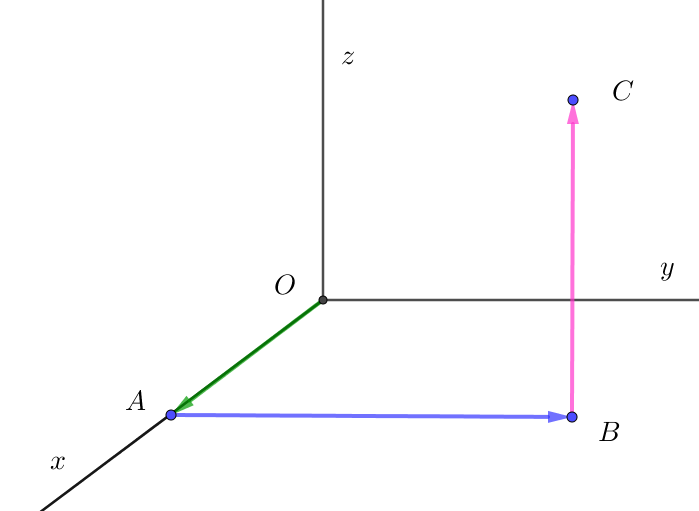
$スカラー場 \quad \phi=x+y+z \quad について、点A(1,\ 0,\ 0),\ \ B(1,\ 2,\ 0),\ C(1,\ 2,\ 3)$
$とする。原点 \ O\ から点 \ C\ に至る折れ線で、線分 \ OA,\ AB,\ BC\ に沿った線積分$
(i)$\ \ 線分 \ OA\ 上では$
$\quad 0 \leqq x \leqq 1,\quad y=0,\quad z=0 $
$\quad このとき \quad \phi=x , \quad ds=dx$
\[\int _{OA} \phi(x,y,z)ds =\int _0^1 xdx=\cfrac{1}{2}\]
(ii)$\ \ 線分 \ AB\ 上では$
$\quad x=1, \quad 0 \leqq y \leqq 2,\quad z=0 $
$\quad このとき \quad \phi=1+y , \quad ds=dy$
\[\int _{AB} \phi(x,y,z)ds =\int _0^2 (1+y)dy=4\]
(ii)$\ \ 線分 \ BC\ 上では$
$\quad x=1, \quad y=2 , \quad 0 \leqq z \leqq 3$
$\quad このとき \quad \phi=1+2+z=3+z , \quad ds=dz$
\[\int _{BC} \phi(x,y,z)ds =\int _0^3 (3+z)dz=\cfrac{27}{2}\]
(i),(ii),(iii)$\ \ より$
\[\int _C \phi(x,y,z)ds =\int _{OA} \phi(x,y,z)ds + \int _{AB} \phi(x,y,z)ds+\int _{BC} \phi(x,y,z)ds= \cfrac{1}{2}+4+\cfrac{27}{2}=18\]
メインメニュー に戻る