フーリェ変換・逆変換
$関数 \ f(x)\ のフーリェ級数は \ f(x)\ が周期関数のときに求められるものでした。$
$では、非周期関数の場合はどうすればいいのでしょうか。$
$考え方は簡単です。周期が無限に大きくなったものと考えればよいのです。$
$区間 \ [-T,\ T]\ で表された周期 \ 2T\ の区分的になめらかな周期関数のフーリェ級数は$
\[f_T(x)=\sum_{n=-\infty}^{\infty} c_ne^{i\scriptsize{\cfrac{n\pi}{T}}\normalsize{x}} \quad ただし \quad c_n=\cfrac{1}{2T}\int_{-T}^T f_T(x)e^{-i\scriptsize{\cfrac{n\pi}{T}}\normalsize{x}}dx\] $\qquad (このことについては$フーリェ級数の複素数表示$を参考にしてください。)$
$c_n \ を \ f_T(x)\ に代入すると$
\[f_T(x)=\sum_{n=-\infty}^{\infty} \Big\{\cfrac{1}{2T}\int_{-T}^T f_T(t)e^{-i\scriptsize{\cfrac{n\pi}{T}}\normalsize{t}}dt \Big\}e^{i\scriptsize{\cfrac{n\pi}{T}}\normalsize{x}} =\cfrac{1}{2\pi}\sum_{n=-\infty}^{\infty} \Big\{\int_{-T}^T f_T(t)e^{-i\scriptsize{\cfrac{n\pi}{T}}\normalsize{t}}dt \Big\}e^{i\scriptsize{\cfrac{n\pi}{T}}\normalsize{x}} \times \cfrac{\pi}{T}\] $ここで \quad \omega_n=\cfrac{n\pi}{T} \quad とおくと \quad \Delta \omega_n=\omega_n-\omega_{n-1}=\cfrac{n\pi}{T}-\cfrac{(n-1)\pi}{T}=\cfrac{\pi}{T}$
$よって$
\[f_T(x)=\cfrac{1}{2\pi}\sum_{n=-\infty}^{\infty} \Big\{\int_{-T}^T f_T(t)e^{-i\omega_nt}dt \Big\}e^{i\omega_nx} \Delta \omega_n\]
$T \longrightarrow \infty \quad とすると \quad \Delta \omega _n \longrightarrow 0 \quad となり、\omega_n \longrightarrow \omega ,\quad f_T(x) \longrightarrow f(x) \quad とすると$
\[f(x)=\lim _{T \rightarrow \infty}f_T(x)=\cfrac{1}{2\pi}\lim _{T \rightarrow \infty} \sum_{n=-\infty}^{\infty} \Big\{\int_{-T}^T f_T(t)e^{-i\omega_nt}dt \Big\}e^{i\omega_nx} \Delta \omega_n\] \[\qquad \lim _{T \rightarrow \infty} \sum_{n=-\infty}^{\infty} \{ \cdots \}\Delta \omega_n \quad の部分は定積分の定義より \quad \int _{-\infty}^{\infty}\big\{ \cdots \big\}d\omega \quad となるから\]
\[f(x)=\cfrac{1}{2\pi}\int _{-\infty}^{\infty}\big(\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \big)e^{i\omega x} d\omega \]
$\hspace{4em} f(x)\ の(\cdots )部分を \ f(x)\ のフーリェ変換といい、F(\omega)\ とかきます。$
\[すなわち \qquad F(\omega)=\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \]
\[このとき \qquad f(x)=\cfrac{1}{2\pi}\int _{-\infty}^{\infty}F(\omega)e^{i\omega x} d\omega \quad をフーリェ逆変換といいます。\]
$なお、工学系ではラプラス変換(そのうち \ up\ する予定です)との関係から$
\[f(x)=\cfrac{1}{\sqrt{2\pi}}\int _{-\infty}^{\infty}\big(\cfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \big)e^{i\omega x} d\omega \quad として\] \[F(\omega)=\cfrac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt \quad を \ f(x)\ のフーリェ変換といい 、\] \[f(x)=\cfrac{1}{\sqrt{2\pi}}\int _{-\infty}^{\infty}F(\omega)e^{i\omega x} d\omega \quad をフーリェ逆変換といいます。\]
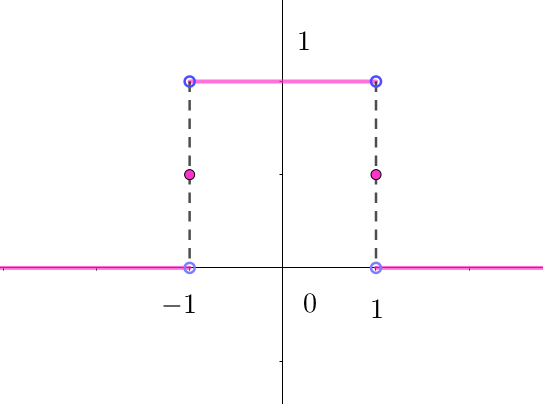
$例 \quad 右図のグラフのような「方形パルス」のフーリェ変換を$
$\qquad 求めてみましょう。$
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
1 \quad (-1 < x < 1\\
\cfrac{1}{2} \quad (x=\pm 1)\\
0 \quad (x < -1 ,\ \ 1 < x)\\
\end{array} \right.
\]
\begin{eqnarray*}
F(\omega)
&=&\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt\\
&=&\int_{-1}^1 e^{-i\omega t}dt\\
&=&-\cfrac{1}{i\omega}\big[e^{-i\omega t}\big]_{-1}^1\\
&=&-\cfrac{1}{i\omega}\big(e^{-i\omega }- e^{i\omega }\big)\\
&=&-\cfrac{1}{i\omega}\big\{(\cos \omega -i\sin \omega )- (\cos \omega +i\sin \omega )\big\}\\
&=&\cfrac{2\sin \omega }{\omega}\\
\end{eqnarray*}
$これを逆変換すると$
\[f(x)=\cfrac{1}{2\pi}\int _{-\infty}^{\infty}F(\omega)e^{i\omega x} d\omega =\cfrac{1}{2\pi}\int _{-\infty}^{\infty}\cfrac{2\sin \omega }{\omega}e^{i\omega x} d\omega
=\cfrac{1}{\pi}\int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega}e^{i\omega x} d\omega\]
$(1)\ \ x=0 \quad とおくと \quad f(0)=1 \quad だから$
\[f(0)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega} d\omega=1 \quad より \quad \int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega} d\omega =\pi\]
\[\cfrac{\sin \omega }{\omega} \quad は偶関数だから \quad \int _0^{\infty}\cfrac{\sin \omega }{\omega} d\omega =\cfrac{\pi}{2}\]
$\qquad これは、$定積分の計算1$の(1)で求めた値に一致します。$
$(2)\ \ 0 < x < 1 \quad のとき \quad f(x)=1 \quad だから$
\[f(x)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega}e^{i\omega x} d\omega=1 \qquad \cfrac{1}{\pi}\int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega}(\cos \omega x+i\sin \omega x) d\omega=1\]
$\qquad \cfrac{\sin \omega }{\omega}\cos \omega x \quad は偶関数、\cfrac{\sin \omega }{\omega}\sin \omega x \quad は奇関数だから$
\[\cfrac{1}{\pi}\int _{-\infty}^{\infty}\cfrac{\sin \omega }{\omega}\cos \omega x d\omega=1\]
\[\int _0^{\infty}\cfrac{\sin \omega }{\omega}\cos \omega x d\omega=\cfrac{\pi}{2}\]
$あらためて x \longrightarrow a \quad とおくと$
\[\int _0^{\infty}\cfrac{\sin \omega \cos a \omega }{\omega} d\omega=\cfrac{\pi}{2} \quad (0 < a < 1)\]
$このような定積分が得られます。$
フーリェ変換メニュー に戻る
メインメニュー に戻る