F分布
1 F分布
$2つの確率変数X_1,X_2が互いに独立に自由度n_1,n_2の\chi ^2 分布にしたがうとき、比 \ \ \cfrac{X_1}{n_1} \big / \cfrac{X_2}{n_2} \ \ で定まる$
$確率変数の密度関数を求めましょう。$
$\quad X= \cfrac{X_1}{n_1} \big / \cfrac{X_2}{n_2}= \cfrac{n_2X_1}{n_1X_2},\quad Y=n_1X_2\ \ と変数変換すると \quad X_2=\cfrac{Y}{n_1},\quad X_1=\cfrac{n_1}{n_2}X_2X=\cfrac{XY}{n_2}$
$X_1,X_2の同時分布f(x_1,x_2)は、X_1,X_2が互いに独立だからf_1(x_1),f_2(x_2)と分離できる。$
$また、変数変換にともなうヤコビアン$ (2つの確率変数の和$を参照してください)は$
$\quad J=\left| \begin{array}{rr} \cfrac{\partial x_1}{\partial x} & \cfrac{\partial x_1}{\partial y} \\ \cfrac{\partial x_2}{\partial x} & \cfrac{\partial x_2}{\partial y} \\ \end{array} \right | =\left| \begin{array}{rr} \cfrac{y}{n_2} & \cfrac{x}{n_2} \\ 0 & \cfrac{1}{n_1} \\ \end{array} \right | =\cfrac{y}{n_1n_2}$
$したがって、 X,Yの同時確率密度関数f(x,y)は$
$\quad f(x,y)=|J|f(x_1,x_2)=|J|f_1(x_1)f_2(x_2)=\cfrac{y}{n_1n_2}f_1(\cfrac{xy}{n_2})f_2(\cfrac{y}{n_1})=\cfrac{y}{n_1n_2}\chi_{n_1}^2(\cfrac{xy}{n_2})\chi_{n_2}^2(\cfrac{y}{n_1})$
$Xの確率密度関数f(x)はこれの周辺分布だから$
\begin{eqnarray*} f(x) &=&\int _0^{\infty}f(x,y)dy\\ \\ &=&\int _0^{\infty}\cfrac{y}{n_1n_2}\chi_{n_1}^2(\cfrac{xy}{n_2})\chi_{n_2}^2(\cfrac{y}{n_1})dy\\ \\ &=&\int _0^{\infty}\cfrac{y}{n_1n_2}\cfrac{1}{2^{\small \dfrac{n_1}{2}}\Gamma(\dfrac{n_1}{2})} \bigl(\cfrac{xy}{n_2}\bigr)^{\small{\dfrac{n_1-2}{2}}}e^{\small{-\dfrac{xy}{2n_2}}} \times \cfrac{1}{2^{\small \dfrac{n_2}{2}}\Gamma(\dfrac{n_2}{2})} \bigl(\cfrac{y}{n_1}\bigr)^{\small{\dfrac{n_2-2}{2}}}e^{\small{-\dfrac{y}{2n_1}}}dy\\ \\ &=&\cfrac{ x^{ \small{\dfrac{n_1-2}{2} } } } { 2^{ \small {\dfrac{n_1+n_2}{2} } } \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_2}{2}) } \times \cfrac{1}{n_1n_2 n_1^{\small{\dfrac{n_2-2}{2}} } n_2^{\small{\dfrac{n_1-2}{2} } } } \int _0^{\infty} y^{1+\small{\dfrac{n_1-2}{2}}+ \small{\dfrac{n_2-2}{2}}} e^{\small{-\dfrac{y}{2}( \dfrac{x}{n_2}+\dfrac{1}{n_1} ) } }dy\\ \\ &=&\cfrac{ x^{ \small{\dfrac{n_1-2}{2} } } } { 2^{ \small {\dfrac{n_1+n_2}{2} } } \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_2}{2}) } \times \cfrac{1}{ n_1^{\small{\dfrac{n_2}{2} } } n_2^{\small{\dfrac{n_1}{2} } } } \int _0^{\infty} y^{\small{\dfrac{n_1+n_2 -2}{2} } } e^{\small{-\dfrac{y}{2}( \dfrac{x}{n_2}+\dfrac{1}{n_1} ) } }dy\\ \end{eqnarray*}
$定積分で \dfrac{y}{2}( \dfrac{x}{n_2}+\dfrac{1}{n_1} )=u \ \ とおくと$
\begin{eqnarray*} I &=&\int _0^\infty e^{-u} \Bigl( \cfrac{2u}{\small {\cfrac{x}{n_2}+\cfrac{1}{n_1}}}\Bigr)^{\small {\dfrac{n_1+n_2-2}{2}} }\times \cfrac{2du}{\small {\cfrac{x}{n_2}+\cfrac{1}{n_1}}}\\ \\ &=&\Bigl( \cfrac{2}{\small {\cfrac{x}{n_2}+\cfrac{1}{n_1}}}\Bigr)^{\small {\dfrac{n_1+n_2}{2}} }\int _0^\infty e^{-u} u^{\small {\dfrac{n_1+n_2-2}{2} }} du\\ \\ &=&\Bigl( \cfrac{2}{\small {\cfrac{x}{n_2}+\cfrac{1}{n_1}}}\Bigr)^{\small {\dfrac{n_1+n_2}{2}} } \Gamma(\dfrac{n_1+n_2}{2}) \\ \end{eqnarray*} $したがって$
\begin{eqnarray*} f(x) &=&\cfrac{ x^{ \small{\dfrac{n_1-2}{2} } } } { 2^{ \small {\dfrac{n_1+n_2}{2} } } \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) } \times \cfrac{1}{ n_1^{\small{\dfrac{n_2}{2} } } n_2^{\small{\dfrac{n_1}{2} } } } \times \Bigl( \small {\cfrac{2}{\cfrac{x}{n_2}+\cfrac{1}{n_1}}}\Bigr)^{\small {\dfrac{n_1+n_2}{2}} } \Gamma(\dfrac{n_1+n_2}{2}) \\ \\ &=&\cfrac{ \Gamma(\dfrac{n_1+n_2}{2}) x^{ \small{\dfrac{n_1-2}{2} } }} { \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) n_1^{\small{\dfrac{n_2}{2} } } n_2^{\small{\dfrac{n_1}{2} } } } \times \Bigl( \cfrac{n_1n_2}{n_1x+n_2}\Bigr)^{\small {\dfrac{n_1+n_2}{2}} } \\ \\ &=&\cfrac{ \Gamma(\dfrac{n_1+n_2}{2}) n_1^{\small{\dfrac{n_1}{2} } } n_2^{\small{\dfrac{n_2}{2} } } } { \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) } \cfrac{ x^{ \small{\dfrac{n_1-2}{2} } } } {(n_1x+n_2)^{ \small{\dfrac{n_1+n_2}{2}}} }\\ \\ &=&\cfrac{ \Gamma(\dfrac{n_1+n_2}{2}) n_1^{\small{\dfrac{n_1}{2} } } n_2^{\small{\dfrac{n_2}{2} } } } { \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) } \cfrac{ x^{ \small{\dfrac{n_1-2}{2} } } } { n_2^{ \small{\dfrac{n_1+n_2}{2} } } (1+\dfrac{n_1}{n_2}x )^{ \small{\dfrac{n_1+n_2}{2}}} }\\ \\ &=&\cfrac{ \Gamma(\dfrac{n_1+n_2}{2}) } { \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) }\bigl(\cfrac{n_1}{n_2}\bigr)^{\small{\dfrac{n_1}{2} } } x^{ \small{\dfrac{n_1-2}{2} } } (1+\dfrac{n_1}{n_2}x )^{ -\small{\dfrac{n_1+n_2}{2} }} \\ \end{eqnarray*}
$これが確率密度関数の条件をみたすことは$
(i)$f(x) > 0 は明らか$
(ii) \[\int _0^\infty f(x)dx=1 \ \ は\] \[I=\int _0^\infty x^{ \small{\dfrac{n_1-2}{2} } } (1+\dfrac{n_1}{n_2}x )^{ -\small{\dfrac{n_1+n_2}{2} }}dx =\int _0^\infty \cfrac{x^{ \small{\dfrac{n_1-2}{2} } }}{ (1+\dfrac{n_1}{n_2}x )^{ \small{\dfrac{n_1+n_2}{2} }}}dx\]
$\cfrac{1}{1+\dfrac{n_1}{n_2}x}=t \ \ とおくと \quad 1+\dfrac{n_1}{n_2}x=\cfrac{1}{t} \ \ より \dfrac{n_1}{n_2}dx=-\cfrac{dt}{t^2}$
\begin{eqnarray*} I &=&\int _1^ 0 \bigl\{ \dfrac{n_2}{n_1}(\cfrac{1}{t}-1)\bigr\} ^{ \small{\dfrac{n_1-2}{2} } } t^{ \small{\dfrac{n_1+n_2}{2} }} \dfrac{n_2}{n_1}(-\cfrac{dt}{t^2})\\ \\ &=&\int _0^ 1 (\dfrac{n_2}{n_1} )^{ \small{\dfrac{n_1-2}{2} }} (\cfrac{1-t}{t})^{ \small{\dfrac{n_1-2}{2} } } t^{ \small{\dfrac{n_1+n_2}{2} }} \dfrac{n_2}{n_1} \cfrac{dt}{t^2}\\ \\ &=&\int _0^ 1 (\dfrac{n_2}{n_1} )^{ \small{\dfrac{n_1}{2} }} (1-t)^{ \small{\dfrac{n_1-2}{2} } } t^{ \small{-\dfrac{n_1-2}{2}+\dfrac{n_1+n_2}{2} -\large{2}}} dt\\ \\ &=& (\dfrac{n_2}{n_1} )^{ \small{\dfrac{n_1}{2} }} \int _0^ 1 (1-t)^{ \small{\dfrac{n_1-2}{2} } } t^{ \small{\dfrac{n_2-2}{2} }} dt\\ \\ &=& (\dfrac{n_2}{n_1} )^{ \small{\dfrac{n_1}{2} }} B(\dfrac{n_2}{2}, \dfrac{n_1}{2})\\ \\ \end{eqnarray*} $よって$
\[\int _0^\infty f(x)dx =\cfrac{ \Gamma(\dfrac{n_1+n_2}{2}) } { \Gamma(\dfrac{n_1}{2}) \Gamma(\dfrac{n_1}{2}) }\bigl(\cfrac{n_1}{n_2}\bigr)^{\small{\dfrac{n_1}{2} } } \times (\dfrac{n_2}{n_1} )^{ \small{\dfrac{n_1}{2} }} B(\dfrac{n_2}{2}, \dfrac{n_1}{2}) =\cfrac{1}{ B(\dfrac{n_2}{2}, \dfrac{n_1}{2})} \times B(\dfrac{n_2}{2}, \dfrac{n_1}{2}) =1\]
$この密度関数をf_{n_1,n_2}(x) とかき、この分布をF分布(スネデカーのF分布あるいはフィッシャー分布)といい、$
$F_{n_ 2} ^{n_1} とかきます。$
$次のグラフは、m=n_1,n=n_2 とおいた代表的なF分布のグラフです。$
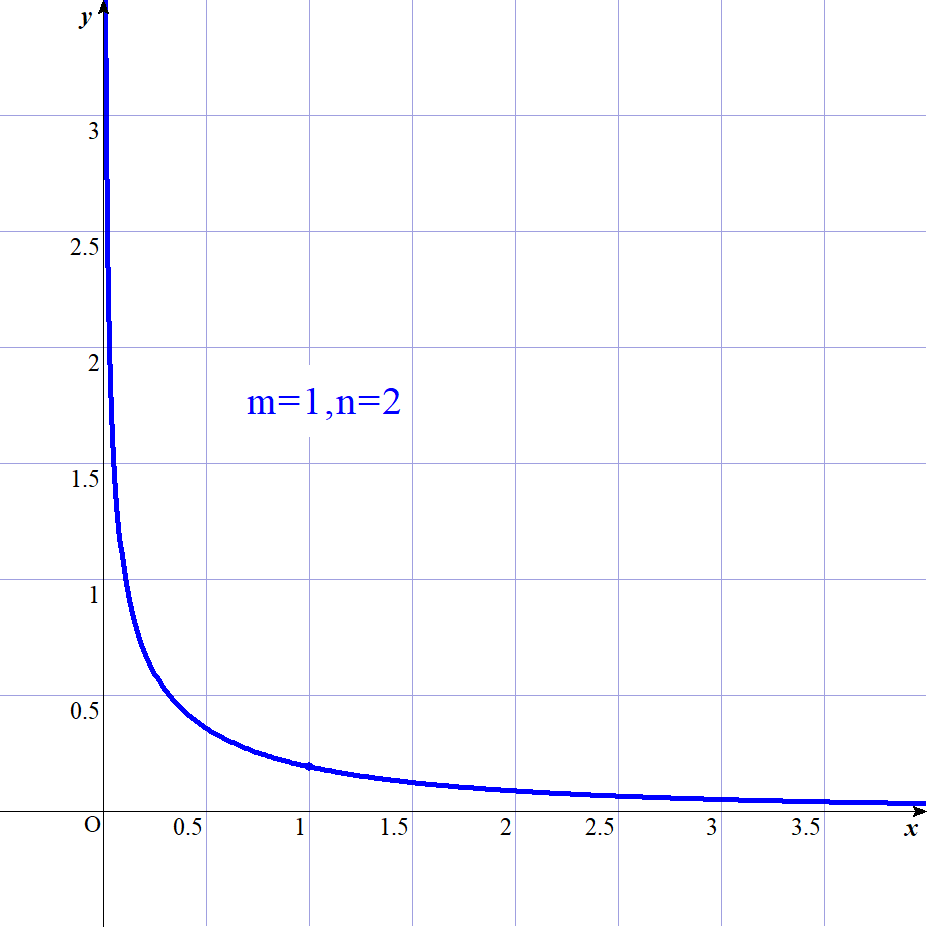
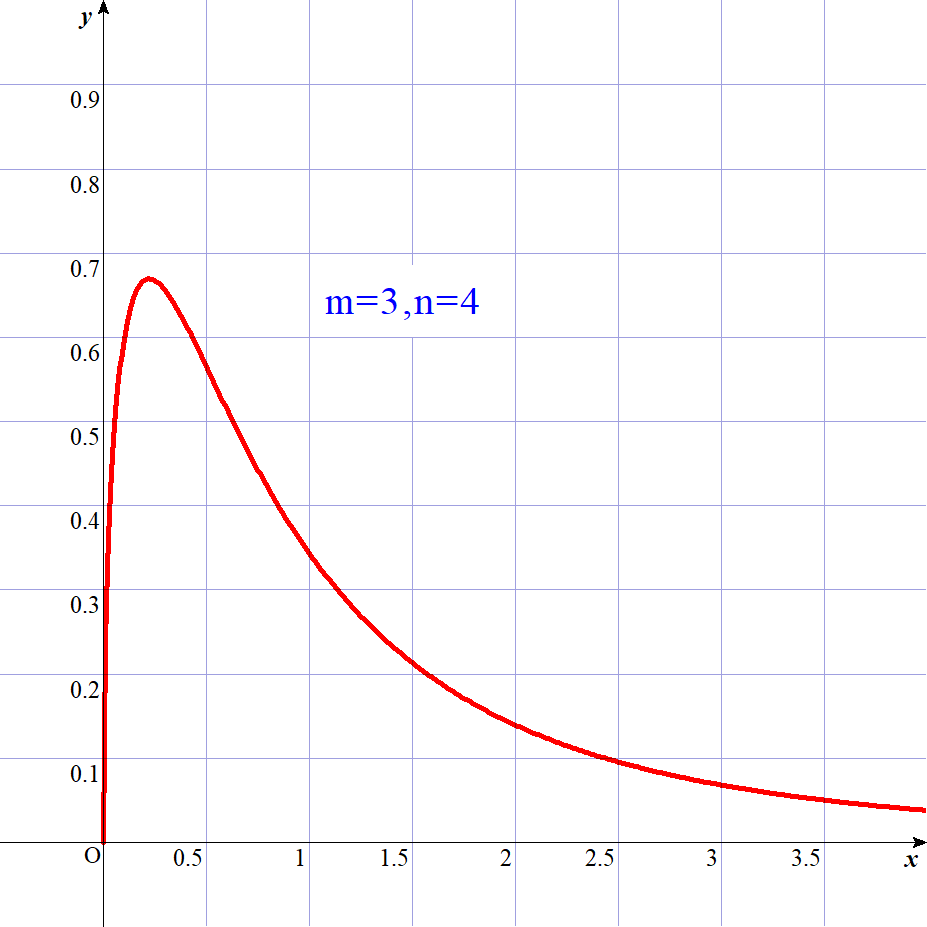
2 F分布にしたがう統計量
$定理1$
$2つの正規母集団N(\mu_1,\sigma_1^2),N(\mu_2,\sigma_2^2)からとった大きさm,nの標本について、標本分散を \ S_1 ^2,\ \ S_2 ^2 \ とすると$
$\quad \cfrac{m(n-1)}{n(m-1)}\cfrac{\sigma _2 ^2}{\sigma _1^2}\cfrac{S_1 ^2}{S_2 ^2} \ \ は自由度 \ (m-1,n-1) \ のF分布にしたがう。$
$(証明)$
$2組の標本は2つの正規母集団からとったものだから$
$\quad U_1=\cfrac{mS_1 ^2}{\sigma _1 ^2} \ \ と \ \ U_2=\cfrac{nS_2 ^2}{\sigma _2 ^2} \ \ は互いに独立で、それぞれ自由度m-1,n-1の\chi ^2分布にしたがう。$
$\hspace{5em}($標本分散$を参照してください)$
$したがって$
$\quad 比 \cfrac{U_1}{m-1} \big / \cfrac{U_2}{n-1} \ \ は自由度(m-1,n-1)のF分布にしたがう。$
$ゆえに$
$\quad \cfrac{mS_1 ^2}{(m-1)\sigma _1 ^2} \big / \cfrac{nS_2 ^2}{(n-1)\sigma _2^2} \ \ は自由度(m-1,n-1)のF分布にしたがう。$
$この定理により、2つの正規母集団の等分散仮説の検定をおこなうことができます。$
$定理2$
$正規母集団N(\mu,\sigma^2)からとった大きさnの標本について$
$\quad \cfrac{(n-1)(\overline{X}-\mu)^2}{S ^2} \ \ は自由度(1,n-1)のF分布にしたがう。$
$(証明)$
$\cfrac{n(\overline{X}-\mu)^2}{\sigma ^2} \ \ は自由度1の\chi ^2分布にしたがい、 \cfrac{nS ^2}{\sigma ^2}\ \ は自由度(n-1)1の\chi ^2分布にしたがうから$
$\hspace{5em}($標本分散$を参照してください)$
$\quad 比 \dfrac{\cfrac{n(\overline{X}-\mu)^2}{\sigma ^2}}{1} \Bigg / \dfrac{\cfrac{nS ^2}{\sigma ^2}}{n-1}=\cfrac{(n-1)(\overline{X}-\mu)^2}{S ^2} $
$は自由度(1,n-1)のF分布にしたがう。$
$この定理は次のt分布につながります。$
メインメニュー に戻る