2つの確率変数の和
$連続型確率変数X,Yは互いに独立で、確率密度関数はそれぞれf(x),g(x)とする。$
$このとき、U=X+Y の確率密度関数を求めてみましょう。$
$解法1$
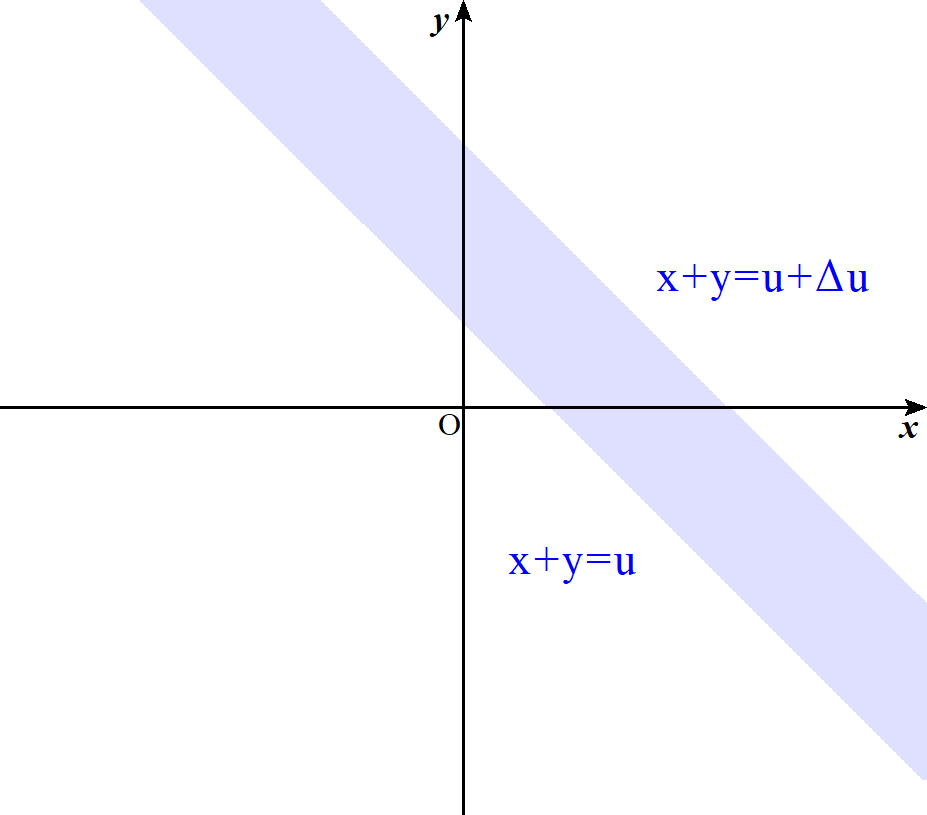
$P(u \leqq U \leqq u+\Delta u)は右図の斜線部分ですが$
$これをy軸に平行な長方形で分割します。$
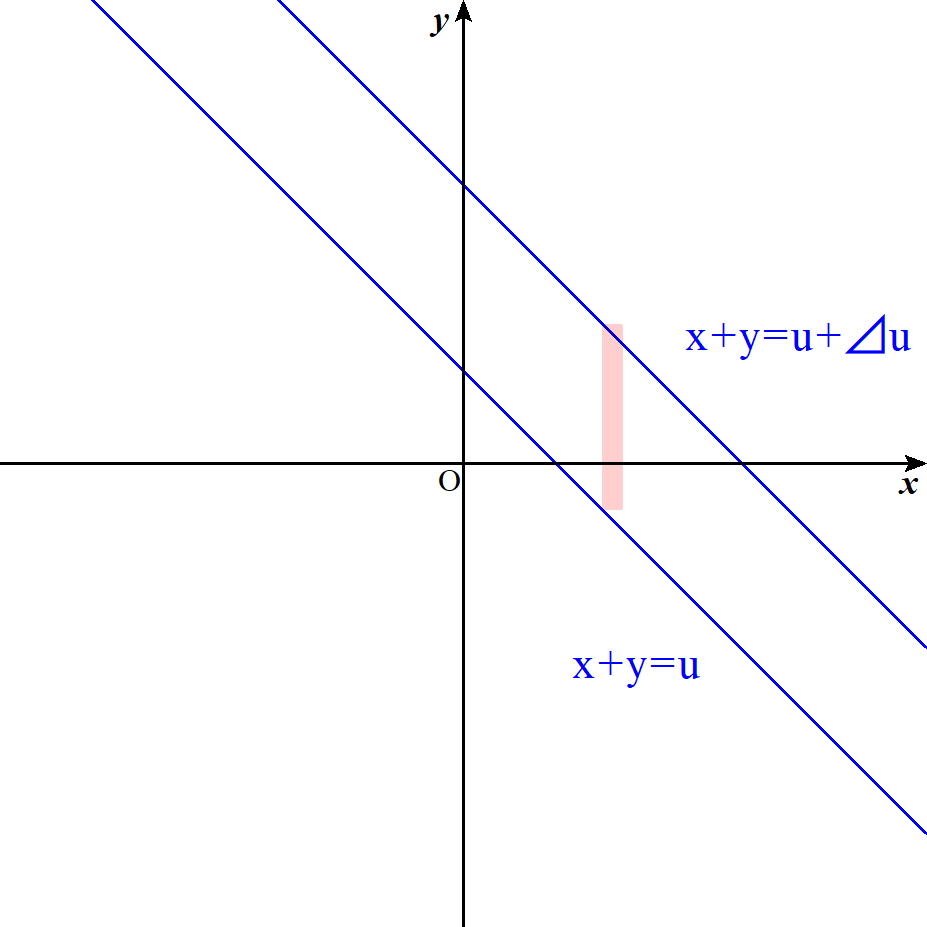
$A_i=\{x_i \leqq X \leqq x_i+\Delta x\}$
$B_i=\{u-x_i \leqq Y \leqq u-x_i+\Delta u\}$
$とすると$
\[P(A_i)=\int _{x_i}^{x_i+\Delta x} f(x)dx\]
\[P(B_i)=\int _{u-x_i}^{u-x_i+\Delta u} g(y)dy\]
$y=z-x_i \ \ とおくと$
\[P(B_i)=\int _u^{u+\Delta u} g(z-x_i)dz\]
$定積分についての平均値の定理より u < u_i < u+\Delta u であるu_i が存在して$
\[\int _u^{u+\Delta u} g(z-x_i)dz=g(u_i-x_i)\Delta u\]
$また、X,Yは互いに独立だから、事象A_iとB_iは独立です。$
\begin{eqnarray*}
P(u \leqq U \leqq u+\Delta u)
&=&\sum_{i} P(A_i \cap B_i)\\
\\
&=&\sum _{i} P(A_i)P(B_i)\\
\\
&=&\int _{-\infty}^{\infty}f(x)dx \ \ g(u-x)\Delta u\\
\\
&=&\Delta u \int _{-\infty}^{\infty}f(x) g(u-x)dx\\
\end{eqnarray*}
$一般に、十分小さい\Delta x について$
$\qquad P(x \leqq X \leqq x + \Delta x)=p(x)\Delta x$
$とあらわされるときp(x)はXの確率密度関数だから$
$Uの確率密度関数は$
\[p(u)=\int _{-\infty}^{\infty}f(x) g(u-x)dx\]
$同様にして$
\[p(u)=\int _{-\infty}^{\infty}f(u-y) g(y)dy\]
$ともあらわされます。これを「f(x)とg(x)の合成積」あるいは「たたきこみ」といいます。$
$\quad U=X+Y\ \ の確率密度関数は$
\[p(u)=\int _{-\infty}^{\infty}f(x) g(u-x)dx \quad あるいは \quad p(u)=\int _{-\infty}^{\infty}f(u-y) g(y)dy\]
$解法2$
$確率変数U,V はX,Yの関数として \quad U=g(X,Y),\quad V=h(X,Y) とあらわされるとする。$
$ただし、(X,Y)と(U,V)は1対1対応で、逆対応 \quad X=\varphi(U,V),\quad Y=\psi(U,V) は連続で、微分可能とします。$
$X,Yの同時確率密度関数をf(x,y)とし、積分での変数変換をおこなうと$
\begin{eqnarray*} P(U \leqq u,V \leqq v) &=&\iint _{\substack{g(x,y) \leqq u \\ h(x,y) \leqq v}}f(x,y)dxdy\\ \\ &=&\int _{-\infty}^u \int _{-\infty}^v f(\varphi(u,v),\psi(u,v))|J|dudv\\ \end{eqnarray*} $ただし、Jはヤコビア ンで\quad J=\left| \begin{array}{rr} \cfrac{\partial x}{\partial u} & \cfrac{\partial x}{\partial v} \\ \cfrac{\partial y}{\partial u} & \cfrac{\partial y}{\partial v} \\ \end{array} \right |$
$したがって$
$\quad (U,V)の確率密度関数は \quad f(\varphi(u,v),\psi(u,v))|J|$
$とくに、X,Yが互いに独立で、f(x,y)=g(x)h(y)\ \ ,u=x+y,\quad v=x \ \ すなわち x=v,\ \ y=u-v \ \ とすると$
$\quad J=\left| \begin{array}{rr} 0 & 1\\ 1 & -1\\ \end{array} \right |=-1 \ \ だから\ \ |J|=1$
$(U,V)の確率密度関数は f(v,u-v) \times 1=g(v)h(u-v)$
$したがって、uの周辺分布は$
\[p(u)=\int _{-\infty}^{\infty}g(v) h(u-v)dv\]
$あらためて、v \rightarrow x,\quad g \rightarrow f,\quad h \rightarrow g \ \ とおきかえて$
\[p(u)=\int _{-\infty}^{\infty}f(x) g(u-x)dx\]
$この証明の方が汎用的で、エレガントですが、2重積分の知識が必要です。$
$以上のことを具体例で確認しましょう。$
$互いに独立な確率変数X,Yがそれぞれ正規分布N(\mu _x,\sigma _x),N(\mu _y,\sigma _y)にしたがうとき$
$U=X+Y \ \ の確率密度関数は$
\begin{eqnarray*} p(u) &=&\int _{-\infty}^{\infty}f(x) g(u-x)dx\\ &=&\int _{-\infty}^{\infty}\cfrac{1}{\sqrt{2\pi}\sigma_x} e^{-\dfrac{1}{2\sigma _x^2}(x-\mu_x)^2} \times \cfrac{1}{\sqrt{2\pi}\sigma_y}e^{-\dfrac{1}{2\sigma _y^2}(u-x-\mu_y)^2}\ \ dx\\ \\ &=&\cfrac{1}{2\pi \sigma_x \sigma_y} \int _{-\infty}^{\infty} e^{-\dfrac{1}{2}\bigl\{\bigl(\dfrac{x-\mu_x}{\sigma _x}\bigr)^2 + \bigl(\dfrac {u-x-\mu_y}{\sigma _y}\bigr)^2\bigr\}} \ \ dx\\ \end{eqnarray*} $被積分関数の指数部分の\{\quad \}は$
$\hspace{3em} \bigl(\cfrac{x-\mu_x}{\sigma _x}\bigr)^2 +\bigl(\cfrac{u-\mu_x-\mu_y-x+\mu_x}{\sigma _y}\bigr)^2$
\begin{eqnarray*} &=&\bigl(\cfrac{x-\mu_x}{\sigma _x}\bigr)^2 +\bigl(\cfrac{u-\mu_x-\mu_y}{\sigma _y}\bigr)^2-2 \times \cfrac {(u-\mu_x-\mu_y)(x-\mu_x)}{\sigma _y ^2}+ \bigl(\cfrac{x-\mu_x}{\sigma _y}\bigr)^2\\ \\ &=&\bigl(\cfrac{1}{\sigma _x ^2} +\cfrac{1}{\sigma _y ^2}\bigr)(x-\mu_x)^2 -2 \times \cfrac {u-\mu_x-\mu_y}{\sigma _y ^2}(x-\mu_x)+ \bigl(\cfrac{u-\mu_x-\mu_y}{\sigma _y}\bigr)^2\\ \\ &=&\cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2} \bigl\{x-\mu _x - \cfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y) \bigr\}^2+ \bigl(\cfrac{u-\mu_x-\mu_y}{\sigma _y}\bigr)^2-\cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2} \times \cfrac{\sigma _x ^4}{(\sigma _x ^2+\sigma _y ^2)^2}(u-\mu_x-\mu_y)^2\\ \\ &=&\cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2} \bigl\{x-\mu _x - \cfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y) \bigr\}^2+ \cfrac{(\sigma _x ^2+\sigma _y ^2)-\sigma _x ^2}{\sigma _y ^2(\sigma _x ^2+ \sigma _y ^2)} \times (u-\mu_x-\mu_y)^2\\ \\ &=&\cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2} \bigl\{x-\mu _x - \cfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y) \bigr\}^2+ \cfrac{1}{\sigma _x ^2 +\sigma _y ^2} (u-\mu_x-\mu_y)^2\\ \end{eqnarray*} $したがって$
\begin{eqnarray*} p(u) &=&\cfrac{1}{2\pi \sigma_x \sigma_y} \int _{-\infty}^{\infty} e^{-\dfrac{1}{2} \Bigl\{\cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2} \bigl(x-\mu _x - \dfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y)\bigr)^2+ \cfrac{1}{\sigma _x ^2 +\sigma _y ^2} (u-\mu_x-\mu_y)^2 \Bigr\}} \ \ dx\\ \\ &=&\cfrac{1}{2\pi \sigma_x \sigma_y} e^{-\dfrac{1}{2} \cfrac{(u-\mu_x-\mu_y)^2 }{\sigma _x ^2+ \sigma _y ^2}} \int _{-\infty}^{\infty} e^{-\dfrac{1}{2} \cfrac{\sigma _x ^2+\sigma _y ^2}{\sigma _x ^2 \sigma _y ^2 } \bigl(x-\mu _x - \dfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y)\bigr)^2}\ \ dx\\ \end{eqnarray*}
$積分項をIとし、\cfrac{\sqrt{\sigma _x ^2+\sigma _y ^2}}{\sqrt{2} \sigma _x \sigma _y }\bigl (x-\mu _x - \cfrac{\sigma _x ^2}{\sigma _x ^2+\sigma _y ^2}(u-\mu_x-\mu_y)\bigr ) =t \ \ とおくと \quad dx=\cfrac {\sqrt{2} \sigma _x \sigma _y }{\sqrt{\sigma _x ^2+\sigma _y ^2}} dt $
\[I= \int _{-\infty}^{\infty} e^{{-t^2}} \times \cfrac {\sqrt{2} \sigma _x \sigma _y }{\sqrt{\sigma _x ^2+\sigma _y ^2}} \ \ dt =\cfrac {\sqrt{2} \sigma _x \sigma _y }{\sqrt{\sigma _x ^2+\sigma _y ^2}} \int _{-\infty}^{\infty} e^{-t^2} dt\] \[\qquad \int _{-\infty}^{\infty} e^{-t^2} dt=\sqrt{\pi} \ \ は\] $\hspace{5em}$ ガウス積分$を参照してください$
$\therefore I=\cfrac {\sqrt{2} \sigma _x \sigma _y }{\sqrt{\sigma _x ^2+\sigma _y ^2}} \times \sqrt{\pi}$
$したがって$
$p(u)=\cfrac{1}{2\pi \sigma_x \sigma_y} e^{-\dfrac{1}{2} \cfrac{(u-\mu_x-\mu_y)^2}{\sigma _x ^2 +\sigma _y ^2} } \times \cfrac {\sqrt{2}\sigma _x \sigma _y }{\sqrt{\sigma _x ^2+\sigma _y ^2}} \times \sqrt{\pi}$
$\sigma=\sqrt{\sigma_x ^2+\sigma_y ^2},\quad \mu=\mu_x-\mu_y \ \ とおくと$
$\qquad p(u)=\cfrac{1}{\sqrt{2\pi} \sigma } e^{-\dfrac{(u-\mu)^2 }{2\sigma ^2}}$
$となり、U=X+Y \ \ は正規分布N(\mu,\sigma ^2)にしたがうことがわかりました。$
$これを、「正規分布の再生性」といいます。$
メインメニュー に戻る