東京大学(理系) 2024年　問題5


$座標空間内に \ 3\ 点 \ A(1,\ 0,\ 0),\ B(0,\ 1,\ 0),\ C(0,\ 0,\ 1)\ をとり、D\ を線分 \ AC\ の中点とする。三角形 \ ABD\ の$
$周および内部を \ x\ 軸のまわりに \ 1\ 回転させて得られる立体の体積を求めよ。$


$(参考)\ \ 類似の問題が$2024年京都府立医科大学問題4$\ \ と \ \ $2024年神戸大学(理系)問題4$で出題されています。$

　

$D\ は線分 \ AC\ の中点だから \ \ D(\dfrac{1}{2},\ 0,\ \dfrac{1}{2})$

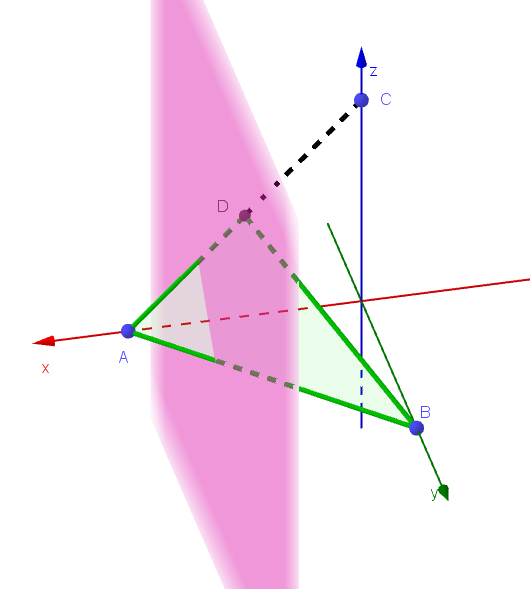
$x\ 軸に垂直な平面を \ H: \ x=t \ \ とする。$

$右図は \ H:x=0.7\ で \ \triangle ABD \ を切断した様子を$

$表したものである。$

$(1)\ \ H \ と \ \triangle ABD\ との交点$

(i)$\ \ 0 \leqq t \leqq 1\ \ のとき、H\ と\ 線分\ AB\ との交点を \ P\ とすると$

$\quad \vec{AB}=(0,\ 1,\ 0)-(1,\ 0,\ 0)=(-1,\ 1,\ 0)$

$\quad \vec{OP}=\vec{OA}+s\vec{AB}=(1,\ 0,\ 0) + s(-1,\ 1,\ 0)=(1-s,\ s,\ 0)$

$\quad 1-s=t \quad だから \quad s=1-t$

$\quad \therefore\ \ P(t,\ 1-t,\ 0)$

(ii)$\ \ \dfrac{1}{2} \leqq t \leqq 1\ \ のとき、H\ と\ 線分\ AD\ との交点を \ Q\ とすると$

$\quad \vec{AD}=(\dfrac{1}{2},\ 0,\ \dfrac{1}{2})-(1,\ 0,\ 0)=(-\dfrac{1}{2},\ 0,\ \dfrac{1}{2})$

$\quad \vec{OQ}=\vec{OA}+u\vec{AD}=(1,\ 0,\ 0)+u(-\dfrac{1}{2},\ 0,\ \dfrac{1}{2})=(1-\dfrac{u}{2},\ 0,\ \dfrac{u}{2})$

$\quad 1-\dfrac{u}{2}=t \quad だから \quad \dfrac{u}{2}=1-t$

$\quad \therefore\ \ Q(t,\ 0,\ 1-t)$

(iii)$\ \ 0 \leqq t \leqq \dfrac{1}{2} \ \ のとき、H\ と\ 線分\ BD\ との交点を \ R\ とすると$

$\quad \vec{BD}=(\dfrac{1}{2},\ 0,\ \dfrac{1}{2})-(0,\ 1,\ 0)=(\dfrac{1}{2},\ -1,\ \dfrac{1}{2})$

$\quad \vec{OR}=\vec{OB}+v\vec{BD}=(0,\ 1,\ 0)+v(\dfrac{1}{2},\ -1,\ \dfrac{1}{2})=(\dfrac{v}{2},\ 1-v,\ \dfrac{v}{2})$

$\quad \dfrac{v}{2}=t \quad だから　\quad v=2t$

$\quad \therefore\ \ R(t,\ 1-2t,\ t)$


$(2)\ \ 切断面の面積$

$以下の図は、三角形 \ ABD\ の3辺を平面 \ H:x=t\ で切断したものを、yz\ 平面に射影した図で、$

$x\ 軸に垂直な平面 \ H\ は \ yz\ 平面に平行だから重なって見える。また、切断された三角形の内部は$

$線分で示される。O'(t,\ 0,\ 0)\ とする。$

(i)$\ \ 0 \leqq t \leqq \dfrac{1}{2} \ \ のとき$

$\quad \vec{PR}=(t,\ 1-2t,\ t)-(t,\ 1-t,\ 0)=(0,\ -t,\ t)$

$\quad O'\ から \ PR\ に下した垂線の足を \ J\ とすると$

$\quad \vec{O'J}=\vec{OP}+\alpha\vec{PR}=(t,\ 1-t,\ 0)+\alpha(0,\ -t,\ t)=(t,\ 1-(1+\alpha)t,\ \alpha t)$

$\quad \vec{PR} \cdot \vec{O'J}=0 \quad だから$

$\quad -t(1-(1+\alpha)t) + t \times \alpha t=0$

$\quad \alpha=\cfrac{1-t}{2t}$

$\quad このとき$

$\quad \vec{O'J}=\big(t,1-(1+\cfrac{1-t}{2t})t,\cfrac{1-t}{2t} \times t\big)=\big(t,\cfrac{1-t}{2},\cfrac{1-t}{2}\big)$

$\quad R\ と \ J\ が一致するとき$

$\quad 1-2t=\cfrac{1-t}{2}, \ \ かつ \ \ t=\cfrac{1-t}{2}$

$\quad これを解いて \quad t=\cfrac{1}{3}$

　

$(ア)\ \ 0 \leqq t \leqq \cfrac{1}{3} \ \ のとき$

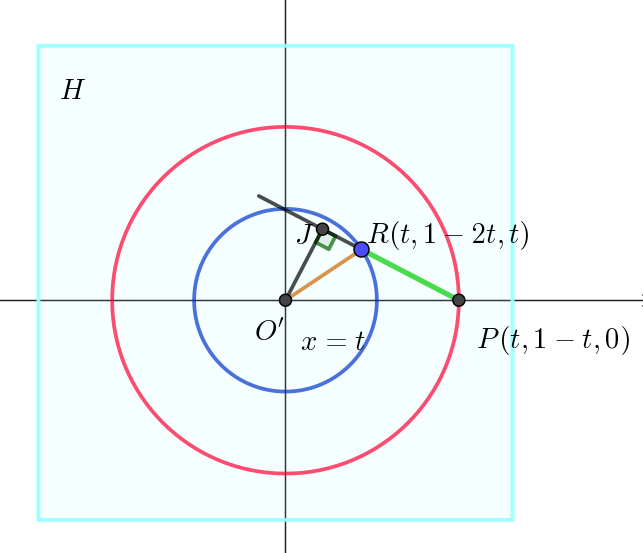
$\quad (1-2t)-\cfrac{1-t}{2}=\cfrac{1-3t}{2} \geqq 0 \quad だから$

$\quad \cfrac{1-t}{2} \leqq 1-2t$

$\quad 点 \ J\ は線分 \ PR\ の外にある。$

$\quad O'\ から最も離れた点 \ P\ が \ O'P=1-t \ \ だから半径 \ 1-t\ の$

$\quad 円(右図の赤い円)を描く。$

$\quad O'\ から最も近い点は \ R\ だから半径 \ O'R \ の円(右図の青い円)を描く$

$\quad したがって、回転体を \ H\ で切断したときの断面積 \ S_1\ は$

$\quad S_1=\pi O'P^2-\pi O'R^2=\pi(1-t)^2-\pi \{(1-2t)^2 +t^2\}=\pi (2t-4t^2)$

　

$(イ)\ \ \cfrac{1}{3} \leqq t \leqq \cfrac{1}{2}\ \ のとき$

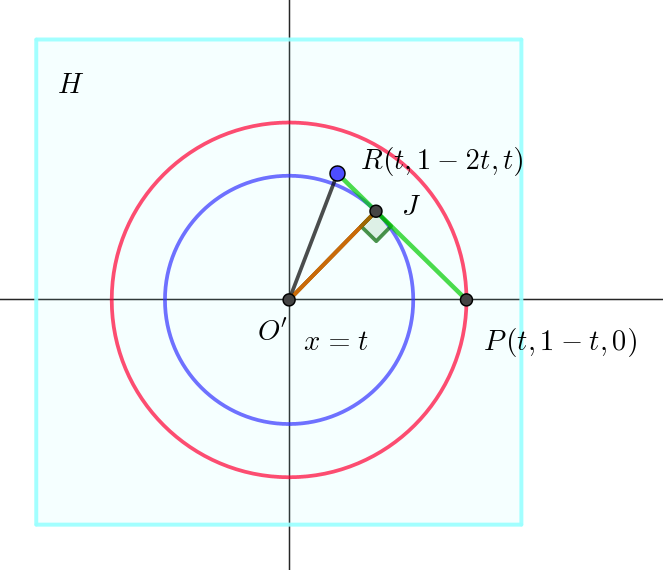
$\quad 点 \ J\ は線分 \ PR\ 上にある。$

$\quad O'\ から最も離れた点 \ P\ が \ O'P=1-t \ だから半径 \ 1-t \ の$

$\quad 円(右図の赤い円)を描く。$

$\quad O'\ から最も近い点は \ J\ だから半径 \ O'J\ の円(右図の青い円)$

$\quadを描く。$

$\quad したがって、回転体を \ H\ で切断したときの断面積 \ S_2\ は$

$\quad S_2=\pi O'P^2-\pi O'J^2=\pi((1-t)^2-\pi \{(\dfrac{1-t}{2})^2 +(\dfrac{1-t}{2})^2\}=\cfrac{\pi}{2}(1-t)^2$

　

(ii)$\ \ \dfrac{1}{2} \leqq t \leqq 1\ \ のとき$

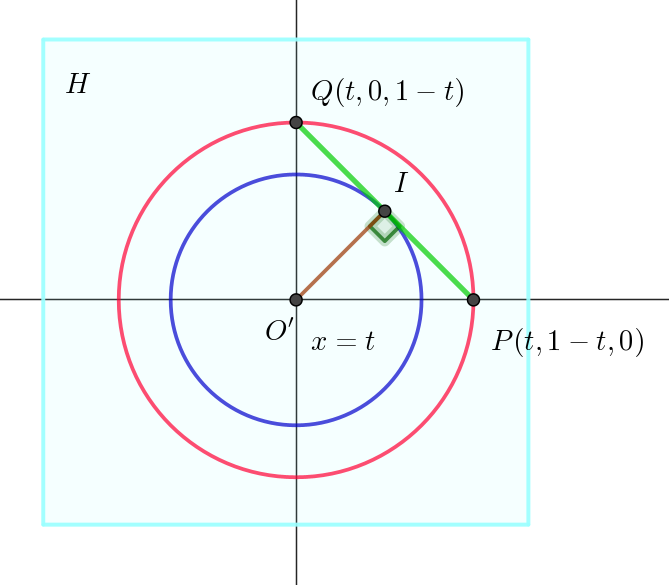
$\quad 切断面は、右図の線分 \ PQ\ である。これが、平面 \ H\ 上で、$

$\quad 点O'(t,\ 0,\ 0)\ で \ 1\ 回転するときにできる図形は$

$\quad O'\ から最も離れた \ 2\ 点 \ P,\ Q\ が \ \ O'P=O'Q=1-t \ \ だから$

$\quad ともに半径 \ 1-t \ の円(右図の赤い円)を描く。$

$\quad O'\ から最も近い点 \ I\ は \ O'\ から \ PQ\ に下した垂線の足だから$

$\quad O'I \perp PQ。$

$\quad \triangle O'PQ \sim \triangle IO'P \ \ で相似比が \ \ \sqrt{2} : 1\ \ だから \ 半径 O'I=\cfrac{1-t}{\sqrt{2}}\ \ の円(右図の青い円)を描く。$

$\quad したがって、回転体を \ H\ で切断したときの断面積 \ S_3\ \ は$

$\quad S_3=\pi O'P^2-\pi O'I^2=\pi(1-t)^2-\pi \times \cfrac{(1-t)^2}{2}=\cfrac{\pi}{2}(1-t)^2$

$\ \ 以上より三角形 \ ABD\ の周および内部を \ x\ 軸のまわりに \ 1\ 回転させて得られる立体の体積 \ V\ は$
\begin{eqnarray*} V &=&\int _0^{\scriptsize{\dfrac{1}{3}}}S_1 dt + \int _{\scriptsize{\dfrac{1}{3}}}^{\scriptsize{\dfrac{1}{2}}} S_2 dt+\int _{\scriptsize{\dfrac{1}{2}}}^1 S_3 dt\\ \\ &=&\int _0^{\scriptsize{\dfrac{1}{3}}}\pi (2t-4t^2) dt + \int _{\scriptsize{\dfrac{1}{3}}}^{\scriptsize{\dfrac{1}{2}}} \cfrac{\pi}{2}(1-t)^2 dt+\int _{\scriptsize{\dfrac{1}{2}}}^1 \cfrac{\pi}{2}(1-t)^2 dt\\ \\ &=&\int _0^{\scriptsize{\dfrac{1}{3}}}\pi (2t-4t^2) dt + \int _{\scriptsize{\dfrac{1}{3}}}^1 \cfrac{\pi}{2}(1-t)^2 dt\\ \\ &=&\pi \big[t^2-\dfrac{4}{3}t^3\big] _0^{\scriptsize{\dfrac{1}{3}}} + \pi \big[-\dfrac{1}{6}(1-t)^3\big] _{\scriptsize{\dfrac{1}{3}}}^1 \\ \\ &=&\big(\cfrac{1}{9}-\cfrac{4}{3} \times \cfrac{1}{27} +\cfrac{1}{6} \times \cfrac{8}{27}\big)\pi\\ \\ &=&\cfrac{\pi}{9} \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る