神戸大学(理系) 2024年 問題4
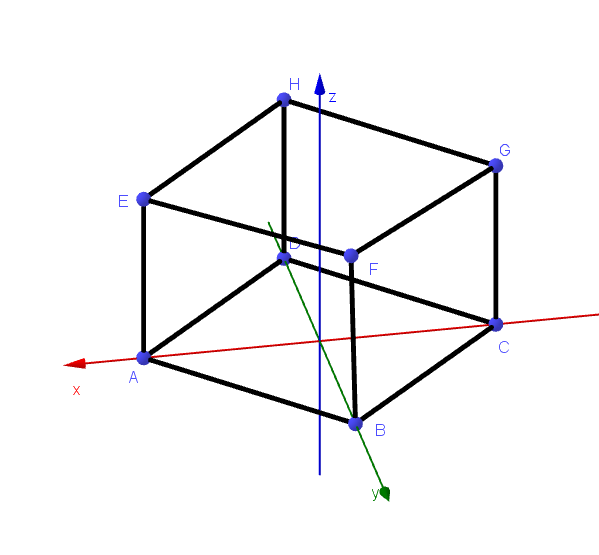
$1\ 辺の長さが \ \sqrt{2}\ の正方形 \ ABCD\ を底面にもち、高さが \ 1\ である直方体 \ ABCD-EFGH\ を、頂点の$
$座標がそれぞれ \ A(1,\ 0,\ 0),\ B(0,\ 1,\ 0),\ C(-1,\ 0,\ 0),\ D(0, -1,\ 0),\ E(1,\ 0,\ 1),\ F(0,\ 1,\ 1),\ G(-1,\ 0,\ 1),$
$\ H(0 -1,\ 1)\ になるように \ xyz\ 空間におく。以下の問に答えよ。$
$(1)\ \ 直方体 \ ABCD-EFGH\ を直線 \ AE\ のまわりに \ 1\ 回転してできる回転体を \ X_1\ とし、また直線 \ AB\ の$
$\quad まわりに \ 1\ 回転してできる回転体を \ X_2\ と \ する。X_1\ の体積 \ V_1\ と \ X_2\ の体積 \ V_2\ を求めよ。$
$(2)\ \ 0 \leqq t \leqq 1\ とする。平面 \ x=t \ と線分 \ EF\ の共有点の座標を求めよ。$
$(3)\ \ 直方体 \ ABCD-EFGH\ を \ x\ 軸のまわりに \ 1\ 回転してできる回転体を \ X_3\ とする。X_3\ の体積V_3を求めよ。$
$(参考)\ \ 類似の問題が$2024年東京大学(理系)問題5$\ \ と \ \ $2024年京都府立医科大学問題4$で出題されています。$
(1)
$X_1\ は回転軸 \ AE\ から最も遠い線分 \ AC=2\ が半径 、$
$高さ \ AE=1 \ の円柱だから$
$V_1=\pi \times 2^2 \times 1=4\pi$
$X_2\ は回転軸 \ AB\ から最も遠い線分が \ GH\ で$
$AH=\sqrt{3}\ が半径 、高さ \ AB=\sqrt{2}\ の円柱だから$
$V_2=\pi \times (\sqrt{3})^2 \times \sqrt{2}=3\sqrt{2}\pi$
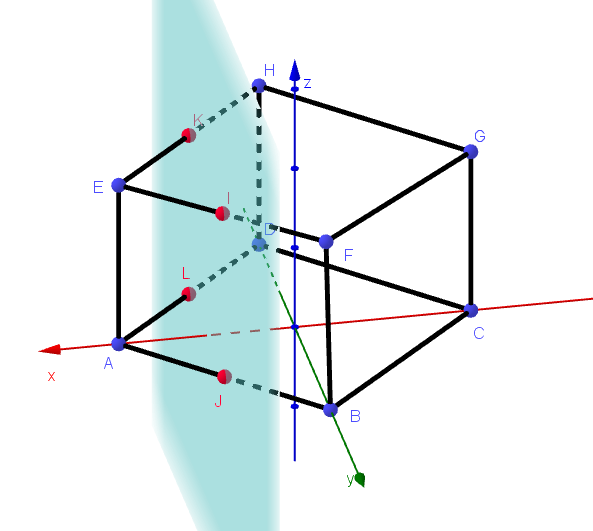
(2)
$平面 \ x=t \ (右図の青い平面)と線分 \ EF\ の共有点を \ I\ とおく。$
$\vec{EF}= (0,\ 1,\ 1)-(1,\ 0,\ 1)=(-1,\ 1,\ 0)$
$\vec{OI}=\vec{OE}+s\vec{EF}=(1,\ 0,\ 1) + s(-1,\ 1,\ 0)=(1-s,\ s,\ 1)$
$1-s=t \quad だから \quad s=1-t$
$\therefore\ \ I(t,\ 1-t,\ 1)$
(3)
$この直方体は平面\ x=0\ すなわち面 \ BFHD\ に関して対称であり、対角線 \ AC\ と \ BD、EG\ と \ FH\ の交点は$
$原点であることから \quad -1 \leqq x \leqq 0 \ \ の部分と \ \ 0 \leqq x \leqq 1 \ \ の部分は対称となる。$
$平面 \ x=t \ と線分 \ AB\ の共有点 \ J\ は、EF /\!/ AB \ \ だから \ \ J(t,\ 1-t,\ 0)$
$平面 \ x=t \ と線分 \ EH\ の共有点を \ K\ とおく。$
$\vec{EH}= (0,-1,\ 1)-(1,\ 0,\ 1)=(-1,-1,\ 0)$
$\vec{OK}=\vec{OE}+u\vec{EH}=(1,\ 0,\ 1) + u(-1,-1,\ 0)=(1-u,-u,\ 1)$
$1-u=t \quad だから \quad u=1-t$
$\therefore\ \ K(t,\ -1+t,\ 1)$
$平面 \ x=t \ と線分 \ AD\ の共有点Lは、AD /\!/ EH \ \ だから \ \ L(t,\ -1+t,\ 0)$
$右図は、直方体 \ ABCD-EFGH\ を平面 \ H:x=t\ で切断したものを、yz\ 平面に射影した図で、$
$x\ 軸に垂直な平面 \ H\ は \ yz\ 平面に平行だから重なって見える。O'(t,\ 0,\ 0)\ とおく$
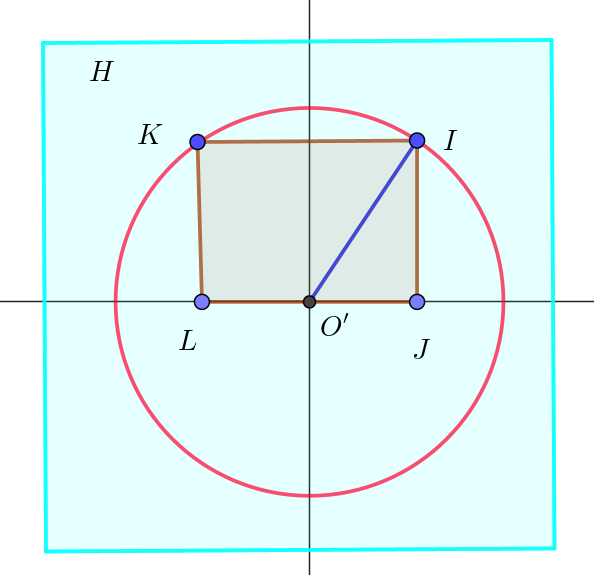
$H\ と交わる辺は、AB,\ AD,\ EF,\ EH \ だから交点は$
$J(t,\ 1-t,\ 0),\quad L(t,\ -1+t,\ 0),\quad I(t,\ 1-t,\ 1),\quad K(t,-1+t,\ 1)$
$O'\ から切断面 \ 四角形JIKL \ への最大の長さは \ O'I=O'K \ だから$
$回転体は半径 \ O'I=O'K\ の円(右図の赤い円)を描く。$
$したがって、回転体を \ H\ で切断したときの断面積 \ S(t)\ は$
$S(t)=\pi O'I^2=\pi\{t^2+(1-t)^2\}=\pi(2-2t+t^2)$
$よって、直方体 \ ABCD-EFGH\ を \ x\ 軸のまわりに \ 1\ 回転してできる回転体 \ X_3\ の体積 \ V_3\ は$
$-1 \leqq t \leqq 0 \ \ の部分と合わせて$
\begin{eqnarray*} V_3 &=& 2\pi \int _0^1 S(t)dt\\ \\ &=&2\pi \int _0^1 (2-2t+t^2)dt\\ \\ &=&2\pi\big[2t-t^2+\dfrac{t^3}{3}\big]_0^1\\ \\ &=&\cfrac{8}{3}\pi \end{eqnarray*}
メインメニュー に戻る