大阪大学(理系) 2025年 問題5
$投げたときに表と裏の出る確率がそれぞれ \ \dfrac{1}{2}\ のコインがある。A,\ B,\ C\ の \ 3\ 文字を \ BAC\ のように \ 1\ 個$
$ずつすべて並べて得られる文字列に対して、コインを投げて次の操作を行う。$
$\ \ ・表が出たら文字列の左から \ 1\ 文字目と \ 2\ 文字目を入れかえる。$
$\ \ ・裏が出たら文字列の左から \ 2\ 文字目と \ 3\ 文字目を入れかえる。$
$例えば、文字列が \ BAC\ であるときに、2\ 回続けてコインを投げて表、裏の順に出たとすると、文字列は$
$BAC\ から \ ABC\ を経て \ ACB\ となる。$
$\ \ 最初の文字列は \ ABC\ であるとする。コインを \ n\ 回続けて投げたあとの文字列が \ ABC\ である確率を \ p_n $
$とし、BCA\ である確率を \ q_n\ とする。$
$(1)\ \ k\ を正の整数とするとき、p_{2k}-q_{2k}\ \ を求めよ。$
$(2)\ \ n\ を正の整数とするとき、p_n \ \ を求めよ。$
$同様の問題が$
2025 一橋大学問題5$および$ 2024 東京大学(理系)第3問 $に出題されていますので参考にしてください。$
(1)
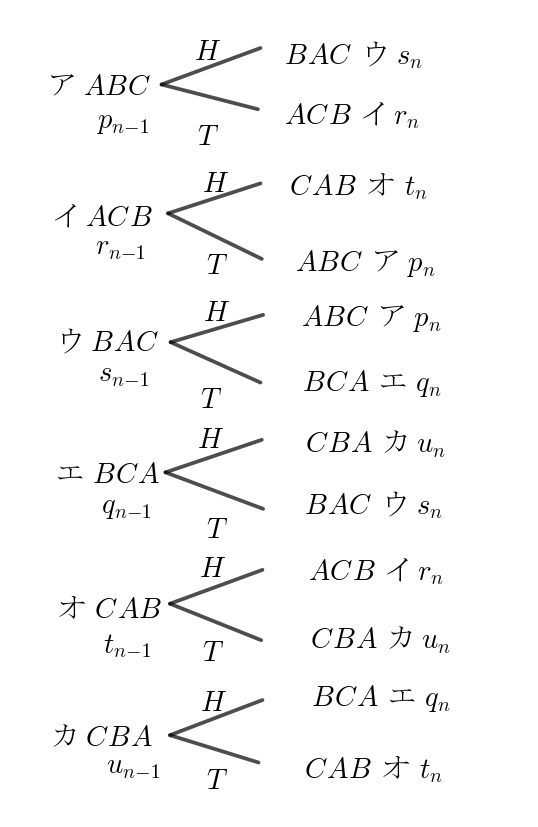
$エ\ (B,\ C,\ A),\ \ オ\ (C,\ A,\ B),\ \ カ\ (C,\ B,\ A)\ \ の \ 6\ 通りある。$
$コインを \ n\ 回続けて投げたあとの文字列がこれになる確率を$
$順に\ \ p_n,\ r_n,\ s_n,\ q_n,\ t_n,\ u_n \ \ とする。$
$右図は、(n-1)回目の試行に続いて、n\ 回目の試行の結果を$
$表したものである。$
$H\ はコインを投げて表、T\ は裏が出る場合である。$
$次の図は、上の樹形図から求めた文字列の推移を示したもので、$
$各辺は双方向に推移できる。$
$E=\{ア,\ エ,\ オ\},\ \ F=\{イ,\ ウ,\ カ\}\ \ のそれぞれの要素は、ある回の$
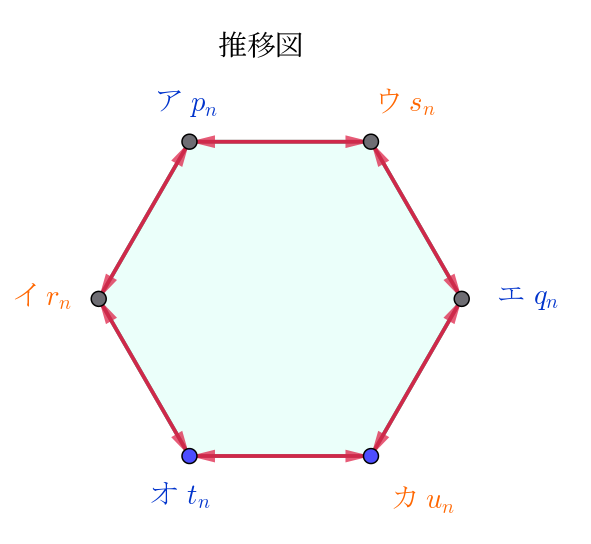
$文字列に推移する。同様に、ある回の試行で、F\ に属する文字列$
$だったとき、次の試行では \ E \ に属する文字列に推移する。$
$最初の文字列が \ ア\ の \ ABC \ だからこれは \ E \ の文字列である。$
$何回かの試行の後、再び \ E \ の文字列に戻るのは、偶数回の試行の$
$あとである。この推移図から、次の漸化式が得られる。$
\[ \hspace{1em} \left\{ \begin{array}{l} p_{2n}=\dfrac{1}{2}r_{2n-1}+\dfrac{1}{2}s_{2n-1} \hspace{5em}①\\ q_{2n}=\dfrac{1}{2}s_{2n-1}+\dfrac{1}{2}u_{2n-1} \hspace{5em}②\\ t_{2n}=\dfrac{1}{2}r_{2n-1}+\dfrac{1}{2}u_{2n-1} \hspace{5em}③\\ r_{2n+1}=\dfrac{1}{2}p_{2n}+\dfrac{1}{2}t_{2n} \hspace{6em}④\\ s_{2n+1}=\dfrac{1}{2}p_{2n}+\dfrac{1}{2}q_{2n}\hspace{6em}⑤\\ u_{2n+1}=\dfrac{1}{2}q_{2n}+\dfrac{1}{2}t_{2n} \hspace{6em}⑥\\ \end{array} \right. \]
$①-②より$
\begin{eqnarray*} & &p_{2k}-q_{2k}\\ \\ &=&\dfrac{1}{2}(r_{2k-1}+s_{2k-1})- \dfrac{1}{2}(s_{2k-1}+u_{2k-1})\\ \\ &=&\dfrac{1}{2}(r_{2k-1}- u_{2k-1})\\ \\ &=&\dfrac{1}{4}(p_{2(k-1)}+t_{2(k-1)})- \dfrac{1}{2}(q_{2(k-1)}+t_{2(k-1)})\\ \\ &=&\dfrac{1}{4}(p_{2(k-1)} - q_{2(k-1)})\\ \\ &=&\big(\dfrac{1}{4}\big)^2(p_{2(k-2)} - q_{2(k-2)})\\ \\ & & \hspace{3em}\vdots \\ \\ &=&\big(\dfrac{1}{4}\big)^k(p_{2(k-k)} - q_{2(k-k)})\\ \\ &=&\big(\dfrac{1}{4}\big)^k(p_0 - q_0)\\ \\ &=&\big(\dfrac{1}{4}\big)^k(1-0)\\ \\ &=&\big(\dfrac{1}{2}\big)^{2k} \end{eqnarray*}
(2)
$F\ の\ ④,\ ⑤,\ ⑥\ を \ E\ の\ ①,\ ②,\ ③\ に代入して$
$2p_{2n}=\dfrac{1}{2}p_{2(n-1)}+\dfrac{1}{2}t_{2(n-1)}+ \dfrac{1}{2}p_{2(n-1)}+\dfrac{1}{2}q_{2(n-1)}=p_{2(n-1)}+\dfrac{1}{2}t_{2(n-1)}+ \dfrac{1}{2}q_{2(n-1)} \hspace{5em}①'$
$2q_{2n}=\dfrac{1}{2}p_{2(n-1)}+\dfrac{1}{2}q_{2(n-1)}+ \dfrac{1}{2}q_{2(n-1)}+\dfrac{1}{2}t_{2(n-1)}=\dfrac{1}{2}p_{2(n-1)}+q_{2(n-1)}+ \dfrac{1}{2}t_{2(n-1)} \hspace{5em}②'$
$2t_{2n}=\dfrac{1}{2}p_{2(n-1)}+\dfrac{1}{2}t_{2(n-1)}+ \dfrac{1}{2}q_{2(n-1)}+\dfrac{1}{2}t_{2(n-1)}=\dfrac{1}{2}p_{2(n-1)}+\dfrac{1}{2}q_{2(n-1)}+ t_{2(n-1)} \hspace{5em}③'$
$①'-②' \ \ より \ \ t_{2(n-1)}\ \ を消去して$
$2p_{2n}-\dfrac{1}{2}p_{2(n-1)}-2q_{2n}+\dfrac{1}{2}q_{2(n-1)}=0 \hspace{7em}⑦$
$①'より \quad t_{2(n-1)}=4p_{2n} -2p_{2(n-1)}-q_{2(n-1)} $
$③'に代入して$
$2(4p_{2(n+1)} -2p_{2n}-q_{2n})=\dfrac{1}{2}p_{2(n-1)}+ \dfrac{1}{2}q_{2(n-1)}+ (4p_{2n} -2p_{2(n-1)}-q_{2(n-1)})$
$8p_{2(n+1)} -8p_{2n}+\dfrac{3}{2}p_{2(n-1)}-2q_{2n}+\dfrac{1}{2}q_{2(n-1)}=0 \hspace{5em}⑧$
$⑧-⑦より$
$8p_{2(n+1)} -10p_{2n}+2p_{2(n-1)}=0$
$p_{2(n+1)} -\dfrac{5}{4}p_{2n}+\dfrac{1}{4}p_{2(n-1)}=0$
$これで、p_{2n} \ \ についての隣接 \ 3\ 項間の漸化式が得られたので$
$p_{2(n+1)} - \alpha \ p_{2n}=\beta (p_{2n} - \alpha \ p_{2(n-1)}) \quad とおくと$
$p_{2(n+1)} - (\alpha + \beta)p_{2n}+ \alpha \beta \ p_{2(n-1)}=0$
$係数を比べて \quad \alpha + \beta=\dfrac{5}{4},\quad \alpha \beta=\dfrac{1}{4}$
$\alpha , \ \ \beta \ \ は \quad w^2-\dfrac{5}{4}w + \dfrac{1}{4}=0 \ \ の解だから$
$4w^2-5w+1=0 \qquad (4w-1)(w-1)=0 \quad の解である。$
$w=\dfrac{1}{4},\quad 1\ \ より \quad \alpha=\dfrac{1}{4},\ \ \beta=1 \quad または \quad \alpha=1 ,\ \ \beta=\dfrac{1}{4}$
(i)$\ \ \alpha=\dfrac{1}{4},\quad \beta=1 \quad のとき$
\begin{eqnarray*} \quad & &p_{2(n+1)} - \dfrac{1}{4}p_{2n}\\ \\ &=&p_{2n} - \dfrac{1}{4}p_{2(n-1)}\\ \\ &=&p_{2(n-1)} - \dfrac{1}{4}p_{2(n-2)}\\ \\ & &\hspace{3em}\vdots \\ \\ &=&p_2-\dfrac{1}{4}p_0\\ \\ &=&\dfrac{1}{2}-\dfrac{1}{4} \times 1\\ \\ &=&\dfrac{1}{4} \end{eqnarray*} $\therefore \ \ p_{2(n+1)} - \dfrac{1}{4}p_{2n}=\dfrac{1}{4}$
(ii)$\ \ \alpha=1 ,\quad \beta=\dfrac{1}{4}\quad のとき$
\begin{eqnarray*} \quad & &p_{2(n+1)} - p_{2n}\\ \\ &=&\dfrac{1}{4}(p_{2n} - p_{2(n-1)})\\ \\ &=&\big(\dfrac{1}{4}\big)^2(p_{2(n-1)} - p_{2(n-2)})\\ \\ & &\hspace{3em}\vdots \\ \\ &=&\big(\dfrac{1}{4}\big)^n(p_2 - p_0)\\ \\ &=&\big(\dfrac{1}{4}\big)^n(\dfrac{1}{2} - 1)\\ \\ &=&-\dfrac{1}{2}\big(\dfrac{1}{4}\big)^n\\ \\ &=&-\big(\dfrac{1}{2}\big)^{2n+1}\\ \end{eqnarray*}
$\therefore \ \ p_{2(n+1)} - p_{2n}=-\big(\dfrac{1}{2}\big)^{2n+1}$
(i) -(ii)$\ \ より$
$\quad \dfrac{3}{4}p_{2n}=\dfrac{1}{4}+\big(\dfrac{1}{2}\big)^{2n+1} \qquad \therefore \ \ p_{2n}=\dfrac{4}{3}\big(\dfrac{1}{4}+\big(\dfrac{1}{2}\big)^{2n+1}\big)= \dfrac{1}{3}\big(1+\big(\dfrac{1}{2}\big)^{2n-1}\big) $
$よって$
\[ \hspace{1em} p_n= \left\{ \begin{array}{l} 0 \quad \hspace{8.5em} (n\ が奇数)\\ \dfrac{1}{3}\big(1+\big(\dfrac{1}{2}\big)^{n-1}\big) \hspace{3em}(n\ が偶数)\\ \end{array} \right. \]
メインメニュー に戻る