一橋大学 2025年 問題5
$5\ 点A,\ B,\ C,\ D,\ E\ が下図のように線分でむすばれている。点P_1,\ P_2,\ P_3,\ \cdots \ を次のように定めていく。$
$P_1\ を \ A\ とする。正の整数 \ n\ に対して、P_n\ を端点とする線分をひとつ無作為にえらび、その線分の \ P_n \ と$
$は異なる端点を \ P_{n+1}\ とする。$
$\hspace{5em}$
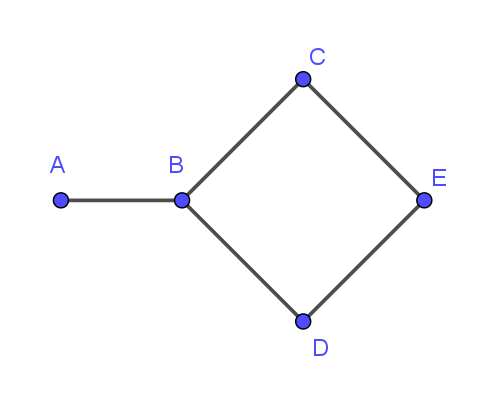
$(1)\ \ P_n \ が \ A\ または \ B\ である確率 \ p_n\ を求めよ。$
$(2)\ \ P_n \ が \ A\ または \ B\ であるとき、k=1,\ 2,\ \cdots , \ n\ のいずれに対しても \ P_k=E\ とならない条件付き確率$
$\quad q_n\ を求めよ。$
$同様の問題が$
2025 大阪大学(理系)問題5$および$ 2024 東京大学(理系)第3問 $に出題されていますので参考にしてください。$
(1)
$P_n が点A,\ B,\ C,\ D,\ E\ である確率をそれぞれ \ a_n,\ b_n,\ c_n,\ d_n,\ e_n \ \ とする。$
$題意より明らかに$
$n\ が奇数のとき \ \ b_n=0,\ \ e_n=0, \qquad n\ が偶数のとき \ \ a_n=0,\ \ c_n=0,\ \ d_n=0$
$a_1=1,\ \ b_2=1$
$図形から、次の漸化式が得られる。$
\[ \hspace{1em} \left\{ \begin{array}{l} a_{n+1}=\dfrac{1}{3}b_n \hspace{10em}①\\ b_{n+1}=a_n+ \dfrac{1}{2}c_n +\dfrac{1}{2}d_n \hspace{4.5em}②\\ c_{n+1}=\dfrac{1}{3}b_n+\dfrac{1}{2}e_n \hspace{7em}③\\ d_{n+1}=\dfrac{1}{3}b_n+\dfrac{1}{2}e_n \hspace{7em}④\\ e_{n+1}=\dfrac{1}{2}c_n+\dfrac{1}{2}d_n\hspace{7em}⑤\\ \end{array} \right. \]
$③、④より \quad c_{n+1}=d_{n+1}$
$これらを$
$②に代入して \quad b_{n+1}=a_n+c_n \hspace{4.5em}②'$
$⑤に代入して \quad e_{n+1}=c_n \hspace{6.5em}⑤'$
$これを③に代入して \quad c_{n+2}=\dfrac{1}{3}b_{n+1}+\dfrac{1}{2}c_n \hspace{7em}③'$
$②'より \quad c_n=b_{n+1}-a_n $
$これを③'に代入して$
$b_{n+3}-a_{n+2}=\dfrac{1}{3}b_{n+1}+\dfrac{1}{2}(b_{n+1}-a_n)$
$b_{n+3}-a_{n+2}=\dfrac{5}{6}b_{n+1}-\dfrac{1}{2}a_n$
$これに①を代入して$
$3a_{n+4}-a_{n+2}=\dfrac{5}{2}a_{n+2}-\dfrac{1}{2}a_n$
$a_{n+4}-\dfrac{7}{6}a_{n+2}+\dfrac{1}{6}a_n=0$
$隣接 \ 3\ 項間の漸化式が得られたので$
$a_{n+4}-\alpha a_{n+2}=\beta(a_{n+2}-\alpha a_n)=0 \quad とおくと$
$a_{n+4}-(\alpha + \beta) a_{n+2} + \alpha \beta a_n=0$
$係数を比較して \quad \alpha + \beta=\dfrac{7}{6},\quad \alpha \beta=\dfrac{1}{6}$
$\alpha, \ \ \beta \ \ は \quad t^2-\dfrac{7}{6}t+\dfrac{1}{6}=0\ \ の解だからこれを解いて \quad t=\dfrac{1}{6},\ \ 1$
$n\ が偶数のときは \ \ a_n=0 \ \ だから \ \ n\ を奇数として$
(i)$ \ \ \alpha=\dfrac{1}{6} ,\quad \beta=1 \quad のとき$
\begin{eqnarray*} & &a_{n+4}-\dfrac{1}{6}a_{n+2}\\ \\ &=&a_{n+2}-\dfrac{1}{6}a_n\\ \\ &=&a_n-\dfrac{1}{6}a_{n-2}\\ \\ & &\hspace{3em}\vdots \\ \\ &=&a_3-\dfrac{1}{6}a_1\\ \\ &=&\dfrac{1}{3}-\dfrac{1}{6}\\ \\ &=&\dfrac{1}{6} \end{eqnarray*}
(ii)$ \ \ \alpha=1 ,\quad \beta=\dfrac{1}{6} \quad のとき$
$\quad a_{n+4}-a_{n+2}=\dfrac{1}{6}(a_{n+2}-a_n) \quad だから$
\begin{eqnarray*} & &a_{n+2}-a_n\\ \\ &=&\dfrac{1}{6}(a_n-a_{n-2})\\ \\ &=&\big(\dfrac{1}{6}\big)^2(a_{n-2}-a_{n-4})\\ \\ & &\hspace{3em}\vdots \\ \\ &=&\big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}(a_3-a_1)\\ \\ &=&\big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}(\dfrac{1}{3}-1)\\ \\ &=&-\dfrac{2}{3}\big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}} \end{eqnarray*}
(i)-(ii)$\ \ より$
$\dfrac{5}{6}a_n=\dfrac{1}{6}+\dfrac{2}{3}\big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}$
$a_n=\dfrac{6}{5}\big\{\dfrac{1}{6}+\dfrac{2}{3}\big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}\big\}=\dfrac{1}{5}\big\{1+4 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}\big\}$
$①に代入して \quad n\ が奇数のときは \ \ b_n=0 \ \ だから \quad n\ が偶数のとき$
$b_n=3a_{n+1}=\dfrac{3}{5}\big\{1+4 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n}{2}}}\big\}=\dfrac{1}{5}\big\{3+2 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-2}{2}}}\big\}$
$したがって\ \ P_n \ が \ A\ または \ B\ である確率 \ p_n\ は$
\[ \hspace{1em} p_n= \left\{ \begin{array}{l} a_n=\dfrac{1}{5}\big\{1+4 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}\big\} \hspace{3.5em} (n\ が奇数のとき)\\ \\ b_n=\dfrac{1}{5}\big\{3+2 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-2}{2}}}\big\} \hspace{4em} (n\ が偶数のとき)\\ \end{array} \right. \]
(2)
$k=1,\ 2,\ \cdots , \ n\ のいずれに対しても \ P_k=E\ とならないとは$
$線分CE,\ \ DE\ \ がなくなるわけでなく、単に \ \ e_k=0 \ \ と考えればよい。$
$したがって、(1)の連立漸化式は$
\[ \hspace{1em} \left\{ \begin{array}{l} a_{n+1}=\dfrac{1}{3}b_n \hspace{10em}①\\ b_{n+1}=a_n+ \dfrac{1}{2}c_n +\dfrac{1}{2}d_n \hspace{4.5em}②\\ c_{n+1}=\dfrac{1}{3}b_n \hspace{10em}③\\ d_{n+1}=\dfrac{1}{3}b_n \hspace{10em}④\\ \end{array} \right. \]
$③、④を②に代入して \quad b_{n+2}=a_{n+1}+\dfrac{1}{3}b_n $
$①を代入して \quad b_{n+2}=\dfrac{1}{3}b_n+\dfrac{1}{3}b_n =\dfrac{2}{3}b_n$
$n\ が奇数のときは \ \ b_n=0 \ \ だから \ \ n\ は偶数として$
$b_n=\dfrac{2}{3}b_{n-2}=\big(\dfrac{2}{3}\big)^2b_{n-4}=\cdots =\big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-2}{2}}}b_{2}=\big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-2}{2}}}$
$①に代入して \quad a_{n+1}=\dfrac{1}{3} \times \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-2}{2}}} \quad だから$
$n\ が奇数のとき \quad a_n=\dfrac{1}{3} \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-3}{2}}}= \dfrac{1}{3} \big(\dfrac{2}{3}\big)^{-1} \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-1}{2}}}=\dfrac{1}{2} \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-1}{2}}}\quad ただし \quad a_1=1$
$よって求める条件付き確率 \ \ q_n\ は$
\[ \hspace{1em} q_n= \left\{ \begin{array}{l} \dfrac{\dfrac{1}{2} \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-1}{2}}}} {\dfrac{1}{5}\big\{1+4 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-1}{2}}}\big\}} \hspace{5em} (n\ が奇数のとき \quad ただし \ \ n=1\ \ のときは \ \ q_1=1)\\ \\ \dfrac{ \big(\dfrac{2}{3}\big)^{\scriptsize{\dfrac{n-2}{2}}}} {\dfrac{1}{5}\big\{3+2 \big(\dfrac{1}{6}\big)^{\scriptsize{\dfrac{n-2}{2}}}\big\}} \hspace{5em} (n\ が偶数のとき)\\ \end{array} \right. \]
メインメニュー に戻る