東京大学(理系) 2024年 問題3
$座標平面上を次の規則\ $(i), (ii)$\ に従って \ 1\ 秒ごとに動く点 \ P\ を考える。$
(i)$\ \ 最初に、P\ は点(2,\ 1)\ にいる。$
(ii)$\ \ ある時刻で \ P\ が点(a,\ b)\ にいるとき、その \ 1\ 秒後には \ P\ は$
$\hspace{3em} ・確率 \ \dfrac{1}{3}\ で \ x\ 軸に関して \ (a,\ b)\ と対称な点$
$\hspace{3em} ・確率 \ \dfrac{1}{3}\ で \ y\ 軸に関して \ (a,\ b)\ と対称な点$
$\hspace{3em} ・確率 \ \dfrac{1}{6}\ で直線 \ y=x\ に関して \ (a,\ b)\ と対称な点$
$\hspace{3em} ・確率 \ \dfrac{1}{6}\ で直線 \ y=-x\ に関して \ (a,\ b)\ と対称な点$
$にいる。$
$以下の問いに答えよ。ただし、(1)については、結論のみを書けばよい。$
$(1)\ \ P\ がとりうる点の座標をすべて求めよ。$
$(2)\ \ n\ を正の整数とする。最初から \ n\ 秒後に \ P\ が点(2,\ 1)\ にいる確率と、最初から \ n\ 秒後に \ P\ が$
$\quad 点(-2,\ -1)\ にいる確率は等しいことを示せ。$
$(3)\ \ n\ を正の整数とする。最初から \ n\ 秒後に \ P\ が点(2,\ 1)にいる確率を求めよ。$
(1)
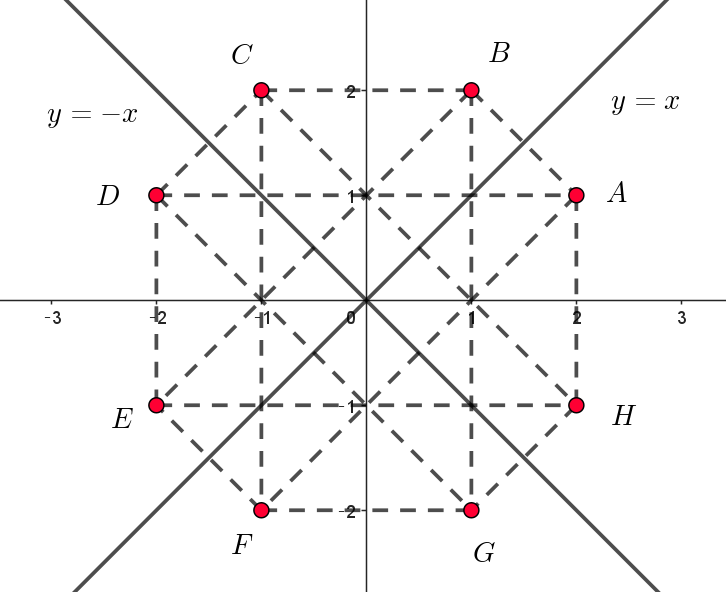
$E(-2,\ -1),\ \ F(-1,\ -2),\ \ G(1,\ -2),\ \ H(2,\ -1)$
$とおくと、これらの点の対称移動先の点の座標は$
$下表のとおりで、この \ 8\ つの点に限る。$
\[ \begin{array}{c||c|c|c|c|c} 点 & \ x\ 軸\ & \ y\ 軸 \ \ & y=x & y=-x \\ \hline A & H & D & B & F\\ \hline B & G & C & A & E\\ \hline C & F & B & H & D\\ \hline D & E & A & G & C\\ \hline E & D & H & F & B\\ \hline F & C & G & E & A\\ \hline G & B & F & D & H\\ \hline H & A & E & C & G\\ \end{array} \]
(2)
$最初から \ n\ 秒後に \ P\ が点A,\ B,\ C,\ D,\ E,\ F,\ G,\ H\ にいるとき、(n+1)\ 秒後の移動先の点とその推移確率は$
$次の表のとおりである。$
\[ \begin{array}{c||c|c|c|c|c} 点 & \ A\ & \ B\ & \ C\ & \ D\ & \ E\ & \ F\ & \ G\ & \ H\ \\ \hline A & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3}\\ \hline B & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0\\ \hline C & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6}\\ \hline D & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0\\ \hline E & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3}\\ \hline F & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0\\ \hline G & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6}\\ \hline H & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0 & \dfrac{1}{3} & 0 & \dfrac{1}{6} & 0\\ \end{array} \]
$最初から \ n\ 秒後に \ P\ が点A,\ B,\ C,\ D,\ E,\ F,\ G,\ H\ にいる確率をそれぞれ$
$a_n,\ b_n,\ c_n,\ d_n,\ e_n,\ f_n,\ g_n,\ h_n \ とする。$
$(1)の表からわかるように、 P\ が \ (n+1)\ 秒後に \ A\ にいるのは、n\ 秒後に \ B,\ D,\ F,\ H \ にいるときだから$
$上の推移確率のAの列をみて$
$a_{n+1}=\cfrac{1}{6}b_n + \cfrac{1}{3}d_n + \cfrac{1}{6}f_n + \cfrac{1}{3}h_n$
$a_1=0$
$a_2=\cfrac{1}{6} \times b_1 + \cfrac{1}{3} \times d_1 + \cfrac{1}{6} \times f_1 + \cfrac{1}{3} \times h_1=\cfrac{1}{6} \times \cfrac{1}{6} + \cfrac{1}{3} \times \cfrac{1}{3} +\cfrac{1}{3} \times \cfrac{1}{3} + \cfrac{1}{6} \times \cfrac{1}{6}=\cfrac{5}{18}$
$同様にして$
$e_{n+1}=\cfrac{1}{6}b_n + \cfrac{1}{3}d_n + \cfrac{1}{6}f_n + \cfrac{1}{3}h_n$
$e_1=0$
$e_2=\cfrac{1}{6} \times b_1 + \cfrac{1}{3} \times d_1 + \cfrac{1}{6} \times f_1 + \cfrac{1}{3} \times h_1=\cfrac{1}{6} \times \cfrac{1}{6} + \cfrac{1}{3} \times \cfrac{1}{3} +\cfrac{1}{3} \times \cfrac{1}{3} + \cfrac{1}{6} \times \cfrac{1}{6}=\cfrac{5}{18}$
$このように、a_n \ と \ e_n\ の初期値と漸化式が等しいので、最初から \ n\ 秒後に \ P\ が点A(2,\ 1)\ にいる確率と、$
$最初から \ n\ 秒後に \ P\ が点E(-2,\ -1)\ にいる確率は等しい。$
(3)
$(2)と全く同様にして$
$b_{n+1}=f_{n+1}=\cfrac{1}{6}a_n + \cfrac{1}{3}c_n + \cfrac{1}{6}e_n + \cfrac{1}{3}g_n$
$b_1=f_1=\cfrac{1}{6}$
$b_2=f_2=\cfrac{1}{6}a_1 + \cfrac{1}{3}c_1 + \cfrac{1}{6}e_1 + \cfrac{1}{3}g_1=0$
$c_{n+1}=g_{n+1}=\cfrac{1}{3}b_n + \cfrac{1}{6}d_n + \cfrac{1}{3}f_n + \cfrac{1}{6}h_n$
$c_1=g_1=0$
$c_2=g_2=\cfrac{1}{3}b_1 + \cfrac{1}{6}d_1 + \cfrac{1}{3}f_1 + \cfrac{1}{6}h_1=\cfrac{1}{3} \times \cfrac{1}{6} + \cfrac{1}{6} \times \cfrac{1}{3} + \cfrac{1}{3} \times \cfrac{1}{6} + \cfrac{1}{6} \times \cfrac{1}{3}=\cfrac{2}{9}$
$d_{n+1}=h_{n+1}=\cfrac{1}{3}a_n + \cfrac{1}{6}c_n + \cfrac{1}{3}e_n + \cfrac{1}{6}g_n$
$d_1=h_1=\cfrac{1}{3}$
$d_2=h_2=\cfrac{1}{3}a_1 + \cfrac{1}{6}c_1 + \cfrac{1}{3}e_1 + \cfrac{1}{6}g_1=0$
$このように、b_n\ と \ f_n,\quad c_n\ と \ g_n,\quad d_n\ と \ h_n \ は初期値と漸化式が等しいので最初から \ n\ 秒後に \ P\ が$
$それぞれの点にいる確率は等しい。$
$したがって \quad A,\ B,\ C,\ D\ の \ 4\ 点について調べればよい。$
\[ \hspace{1em} \left\{ \begin{array}{l} a_{n+1}=\cfrac{1}{3}b_n + \cfrac{2}{3}d_n \hspace{5em}①\\ b_{n+1}=\cfrac{1}{3}a_n + \cfrac{2}{3}c_n \hspace{5em}②\\ c_{n+1}=\cfrac{2}{3}b_n + \cfrac{1}{3}d_n \hspace{5em}③\\ d_{n+1}=\cfrac{2}{3}a_n + \cfrac{1}{3}c_n \hspace{5em}④\\ \end{array} \right. \]
$①と③で \ n \longrightarrow n+1 \ \ とした式に④を代入して$
$a_{n+2}=\cfrac{1}{3}b_{n+1} + \cfrac{2}{3}\big(\cfrac{2}{3}a_n + \cfrac{1}{3}c_n\big)=\cfrac{4}{9}a_n + \cfrac{1}{3}b_{n+1} + \cfrac{2}{9}c_n \hspace{5em}⑤$
$c_{n+2}=\cfrac{2}{3}b_{n+1} + \cfrac{1}{3}\big(\cfrac{2}{3}a_n + \cfrac{1}{3}c_n\big)=\cfrac{2}{9}a_n + \cfrac{2}{3}b_{n+1} + \cfrac{1}{9}c_n \hspace{5em}⑥$
$⑤と⑥に②を代入して$
$a_{n+2}=\cfrac{4}{9}a_n + \cfrac{1}{3}\big(\cfrac{1}{3}a_n + \cfrac{2}{3}c_n\big) + \cfrac{2}{9}c_n =\cfrac{5}{9}a_n + \cfrac{4}{9}c_n \hspace{5em}⑦$
$c_{n+2}=\cfrac{2}{9}a_n + \cfrac{2}{3}\big(\cfrac{1}{3}a_n + \cfrac{2}{3}c_n\big) + \cfrac{1}{9}c_n =\cfrac{4}{9}a_n + \cfrac{5}{9}c_n \hspace{5em}⑧$
$⑦より \quad \cfrac{4}{9}c_n =a_{n+2} - \cfrac{5}{9}a_n $
$c_n =\cfrac{9}{4}a_{n+2} - \cfrac{5}{4}a_n \hspace{5em}⑨$
$⑨を \ \ n \longrightarrow n+ 2 \ \ とすると$
$c_{n+2} =\cfrac{9}{4}a_{n+4} - \cfrac{5}{4}a_{n+2} \hspace{5em}⑩$
$⑧に⑨、⑩を代入して$
$\cfrac{9}{4}a_{n+4} - \cfrac{5}{4}a_{n+2}=\cfrac{4}{9}a_n + \cfrac{5}{9}\big(\cfrac{9}{4}a_{n+2} - \cfrac{5}{4}a_n\big)$
$\cfrac{9}{4}a_{n+4} - \cfrac{5}{2}a_{n+2} + \cfrac{1}{4}a_n =0$
$9a_{n+4} - 10a_{n+2} + a_n =0$
$9(a_{n+4} - a_{n+2})=a_{n+2}- a_n $
$a_{n+4} - a_{n+2}=\cfrac{1}{9}(a_{n+2}- a_n) $
(i)$\ \ n\ が奇数のとき$
$\quad a_1=0,\quad b_2=d_2=0 \quad だから$
$\quad ①より \quad a_3=\cfrac{1}{3}b_2 + \cfrac{2}{3}d_2=0$
$\quad 9a_{n+4}=10a_{n+2} + a_n \quad より順次 \quad a_5=0,\ \ a_7=0 ,\ \ \cdots $
$\quad 一般に \ \ a_n=0\ \ (数学的帰納法で証明する)$
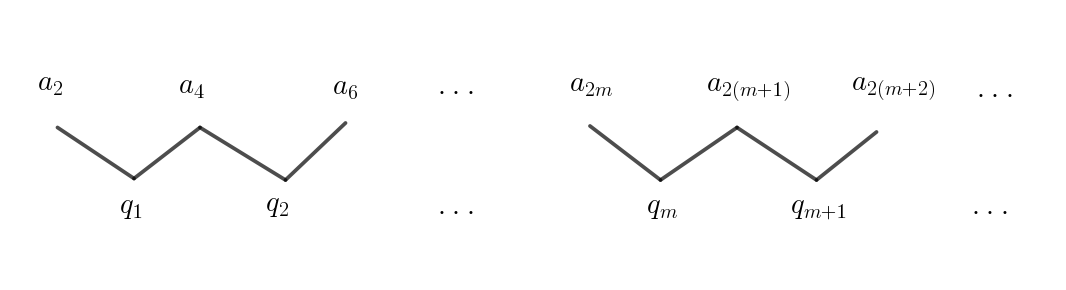
$\quad n=2m$
$\quad a_{2(m+1)}- a_{2m}=q_m \quad とおくと$
$\quad a_{2(m+2)} - a_{2(m+1)}=\cfrac{1}{9}(a_{2(m+1)}- a_{2m})\quad より $
$\quad q_{m+1}=\cfrac{1}{9}q_m$
$\quad 初期値は \quad a_2=\cfrac{5}{18}$
$\quad ⑦より \quad a_4=\cfrac{5}{9}a_2 + \cfrac{4}{9}c_2=\cfrac{5}{9} \times \cfrac{5}{18} + \cfrac{4}{9} \times \cfrac{2}{9}=\cfrac{41}{162}$
$\quad q_1=a_4-a_2=\cfrac{41}{162}-\cfrac{5}{18}=-\cfrac{2}{81}$
$\quad したがって$
$\quad q_m=-\cfrac{2}{81}\big(\dfrac{1}{9}\big)^{m-1}=-\cfrac{2}{9}\big(\dfrac{1}{9}\big)^m$
\begin{eqnarray*} \quad a_{2m} &=&a_2+(q_1+q_2+ \cdots +q_{m-1})\\ \\ &=&\cfrac{5}{18} - \sum _{k=1}^{m-1}\cfrac{2}{9}\big(\dfrac{1}{9}\big)^k\\ \\ &=&\cfrac{5}{18} - \cfrac{2}{9} \times \cfrac{\dfrac{1}{9}\big\{1-(\dfrac{1}{9})^{m-1}\big\}}{1-\dfrac{1}{9}}\\ \\ &=&\cfrac{5}{18} - \cfrac{1}{36} \big\{1-(\dfrac{1}{9})^{m-1}\big\}\\ \\ &=&\cfrac{5}{18} - \cfrac{1}{36} + \cfrac{1}{36} (\dfrac{1}{9})^{m-1}\\ \\ &=&\cfrac{1}{4}+ \cfrac{1}{4} (\dfrac{1}{9})^m\\ \\ &=&\cfrac{1}{4}\big(1+\dfrac{1}{3^{2m}}\big)\\ \end{eqnarray*} $\quad \therefore \ \ a_n=\cfrac{1}{4}\big(1 + \dfrac{1}{3^n}\big)$
$以上より$
$最初から \ n\ 秒後に \ P\ が点(2,\ 1)にいる確率 \ a_n \ は \ \ n\ が奇数のとき \ \ 0,\quad 偶数のとき \ \ \cfrac{1}{4}\big(1 + \dfrac{1}{3^n}\big) \ \ をまとめて$
\begin{eqnarray*} a_n &=&\cfrac{1}{2}(1+(-1)^n) \times \cfrac{1}{4}\big(1+ \dfrac{1}{3^n}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^n) \big(1+ \dfrac{1}{3^n}\big)\\ \end{eqnarray*}
$(補充)$
$最初から \ n\ 秒後に \ P\ が点(-1,\ 2)\ にいる確率 \ c_n \ は⑨より$
\begin{eqnarray*} c_n &=&\cfrac{9}{4}a_{n+2} - \cfrac{5}{4}a_n\\ \\ &=&\cfrac{9}{4}\times \cfrac{1}{8}(1+(-1)^{n+2}) \big(1+ \dfrac{1}{3^{n+2}}\big)- \cfrac{5}{4}\times \cfrac{1}{8}(1+(-1)^n) \big(1+ \dfrac{1}{3^n}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big\{\cfrac{9}{4} \big(1+ \dfrac{1}{3^{n+2}}\big)- \cfrac{5}{4}\big(1+ \dfrac{1}{3^n}\big)\big\}\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big(1+\cfrac{1}{4}\times \dfrac{1}{3^n} - \cfrac{5}{4} \times \dfrac{1}{3^n}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big(1- \dfrac{1}{3^n}\big)\\ \\ \end{eqnarray*} $最初から \ n\ 秒後に \ P\ が点(1,\ 2)\ にいる確率 \ b_n\ は②より$
\begin{eqnarray*} b_{n+1} &=&\cfrac{1}{3}a_n + \cfrac{2}{3}c_n\\ \\ &=&\cfrac{1}{3}\times \cfrac{1}{8}(1+(-1)^n) \big(1+ \dfrac{1}{3^n}\big)+ \cfrac{2}{3}\times \cfrac{1}{8}(1+(-1)^n) \big(1- \dfrac{1}{3^n}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big\{\cfrac{1}{3} \big(1+ \dfrac{1}{3^n}\big) + \cfrac{2}{3}\big(1- \dfrac{1}{3^n}\big)\big\}\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big(1+\dfrac{1}{3^{n+1}} - \dfrac{2}{3^{n+1}}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^{n+2})\big(1- \dfrac{1}{3^{n+1}}\big)\\ \\ \end{eqnarray*} $\therefore \ \ b_n=\cfrac{1}{8}(1+(-1)^{n+1})\big(1- \dfrac{1}{3^n}\big)$
$最初から \ n\ 秒後に \ P\ が点(-2,\ 1)\ にいる確率 \ d_n \ は④より$
\begin{eqnarray*} d_{n+1} &=&\cfrac{2}{3}a_n + \cfrac{1}{3}c_n\\ \\ &=&\cfrac{2}{3}\times \cfrac{1}{8}(1+(-1)^n) \big(1+ \dfrac{1}{3^n}\big)+ \cfrac{1}{3}\times \cfrac{1}{8}(1+(-1)^n) \big(1- \dfrac{1}{3^n}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big\{\cfrac{2}{3} \big(1+ \dfrac{1}{3^n}\big) + \cfrac{1}{3}\big(1- \dfrac{1}{3^n}\big)\big\}\\ \\ &=&\cfrac{1}{8}(1+(-1)^n)\big(1+\dfrac{2}{3^{n+1}} - \dfrac{1}{3^{n+1}}\big)\\ \\ &=&\cfrac{1}{8}(1+(-1)^{n+2})\big(1+ \dfrac{1}{3^{n+1}}\big)\\ \\ \end{eqnarray*} $\therefore \ \ d_n=\cfrac{1}{8}(1+(-1)^{n+1})\big(1+ \dfrac{1}{3^n}\big)$
$(研究)$
$この設問は、「有限マルコフ連鎖」とよばれる確率過程の問題です。$
$(2)で示した、推移確率表を行列で表すと、この行列の固有値を求める問題となります。$
メインメニュー に戻る