MY MATH NOTE

凸関数の不等式

$区間 \ [a,\ b]\ で、関数 \ f(x) が、任意の \ x_1,\ x_2\ について、\alpha_1 \geqq 0,\ \alpha _2 \geqq 0,\ \alpha _1 +\alpha _2 =1 \ \ である \ \alpha _1, \alpha _2 \ に対して$
$\quad \alpha _1 f(x_1)+\alpha _2 f(x_2) \geqq f(\alpha _1 x_1 + \alpha _2 x_2)$
$がなりたつとき、f(x)\ はこの区間で凸関数であるという。$

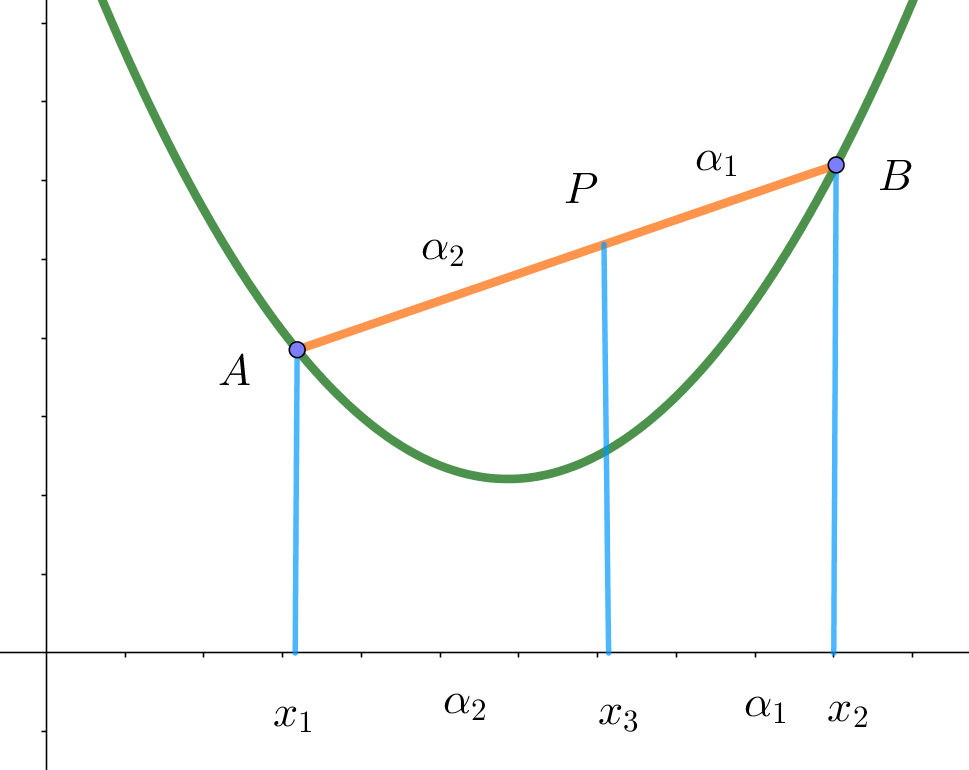
$イメージとしては、$

$A(x_1,\ f(x_1)),\ B(x_2,\ f(x_2))\ とし、線分 \ AB\ を \ \alpha _2 : \alpha _1\ に$

$内分する点 \ P\ の座標 \ (x_3,\ y_3)\ は$

$\qquad x_3=\alpha _1 x_1+\alpha _2 x_2 ,\quad y_3=\alpha _1 f(x_1)+\alpha _2 f(x_2)$

$だから、弦 \ AB\ が弧 \ AB\ の上にあるということです。$


$2\ \ 定理１$

$関数 \ f(x)\ は区間\ [a,\ b]\ で \ 2\ 回微分可能で、f''(x) \geqq 0 \ \ ならば\ \ f(x)\ はこの区間で凸関数である。$

$\quad 関数 \ f(x)\ が区間 \ [a,\ b]\ で凸関数ならば、この区間内の任意の \ x_1,\ x_2,\ \cdots ,\ x_n\ について$
$\qquad \alpha _i \geqq 0 \ \ (i=1,\ 2,\ \cdots,n) ,\ \ \alpha _1 +\alpha _2+\cdots + \alpha _n =1 \ \ である任意の \ \alpha _1,\ \alpha _2,\ \alpha _3\ \ に対して$
$\hspace{3em} \alpha _1f(x_1)+\alpha _2f(x_2)+\cdots +\alpha _nf(x_n) \geqq f(\alpha _1x_1+\alpha _2 x_2+ \cdots +\alpha _n x_n)$

　
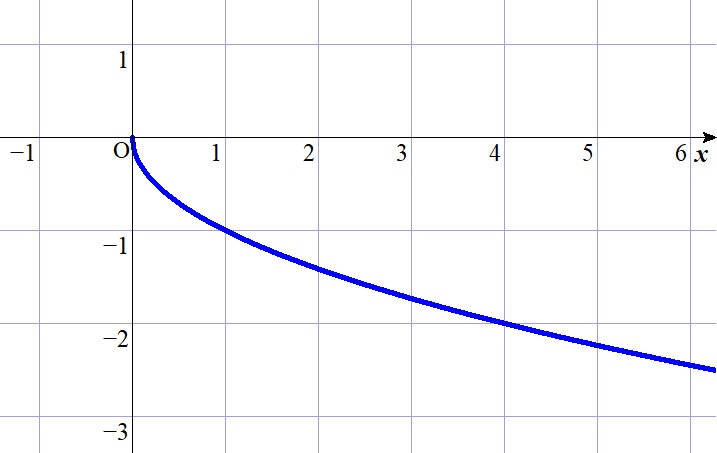
$f(x)=-\sqrt{x}\ \ は \ x \geqq 0 \ で凸関数だから$

$\qquad \alpha _1f(x_1)+\alpha _2f(x_2)+\cdots +\alpha _nf(x_n) \geqq f(\alpha _1x_1+\alpha _2 x_2+ \cdots +\alpha _n x_n)$

$したがって$

$\qquad \alpha _1(-\sqrt{x_1})+\alpha _2(-\sqrt{x_2}) +\cdots +\alpha _n(-\sqrt{x_n})\geqq -\sqrt{\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n}$

$\qquad \therefore \ \ \sqrt{\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n} \geqq \alpha _1 \sqrt{x_1} +\alpha _2 \sqrt{x_2} +\cdots +\alpha _n \sqrt{x_n} $

$(直接証明)$

(i)$は$
\begin{eqnarray*} & &(\sqrt{\alpha _1 x_1 + \alpha _2 x_2})^2-(\alpha _1\sqrt{x_1}+\alpha _2\sqrt{x_2})^2\\ \\ &=&\alpha _1 x_1+ \alpha _2 x_2-(\alpha _1^2 x_1+2\alpha _1 \alpha _2\sqrt{x_1}\sqrt{x_2}+\alpha _2^2 x_2)\\ \\ &=&\alpha _1(1-\alpha _1)x_1-2\alpha _1 \alpha _2\sqrt{x_1}\sqrt{x_2}+\alpha _2(1-\alpha _2)x_2\\ \\ &=&\alpha _1 \alpha _2 x_1-2\alpha _1 \alpha _2\sqrt{x_1}\sqrt{x_2}+\alpha _2 \alpha _1 x_2\\ \\ &=&\alpha _1 \alpha _2(\sqrt{x_1}-\sqrt{x_2})^2\\ \\ &\geqq& 0 \end{eqnarray*}
(ii)$は$
\begin{eqnarray*} & &(\sqrt{\alpha _1 x_1 + \alpha _2 x2+\alpha _3 x_3})^2-(\alpha _1\sqrt{x_1}+\alpha _2\sqrt{x_2}+\alpha _2 \sqrt{x_3})^2\\ \\ &=&\alpha _1 \alpha _2(\sqrt{x_1}-\sqrt{x_2})^2+\alpha _1 \alpha _3(\sqrt{x_1}-\sqrt{x_3})^2+\alpha _2 \alpha _3(\sqrt{x_2}-\sqrt{x_3})^2\\ \\ &\geqq 0& \end{eqnarray*}
(iii)$は$

$\hspace{3em}(\sqrt{\alpha _1 x_1 + \alpha _2 x2+\cdots +\alpha _n x_n})^2-(\alpha _1\sqrt{x_1}+\alpha _2\sqrt{x_2}+\cdots +\alpha _n \sqrt{x_n})^2$

$\hspace{3em}=\alpha _1 \alpha _2(\sqrt{x_1}-\sqrt{x_2})^2+\alpha _1 \alpha _3(\sqrt{x_1}-\sqrt{x_3})^2+\cdots +\alpha _1 \alpha _n(\sqrt{x_1}-\sqrt{x_n})^2$

$\hspace{13em} +\alpha _2 \alpha _3(\sqrt{x_2}-\sqrt{x_3})^2+\cdots +\alpha _2 \alpha _n(\sqrt{x_2}-\sqrt{x_n})^2$
$\hspace{15em} \vdots $
$\hspace{25em} +\alpha _{n-1} \alpha _n(\sqrt{x_{n-1}}-\sqrt{x_n})^2$
$\hspace{3em}\geqq 0$


$例2 \quad 対数関数$

(i)$\ \ \alpha _1,\ \alpha _2,\ x_1,\ x_2 \ が正数で、\alpha _1+\alpha _2=1 \ \ のとき$

$\qquad \log{(\alpha _1 x_1+\alpha _2 x_2)} \geqq \alpha _1\log{x_1}+\alpha _2\log{x_2}$

(ii)$\ \ \alpha _1,\ \alpha _2,\ \cdots ,\ \alpha _n,\ x_1,\ x_2,\ \cdots ,\ x_n \ が正数で、\alpha _1+\alpha _2 +\cdots +\alpha _n=1 \ \ のとき$

$\qquad \log{(\alpha _1 x_1+\alpha _2 x_2+\cdots + \alpha _n x_n)} \geqq \alpha _1\log{x_1}+\alpha _2\log{x_2}+ \cdots +\alpha _n\log{x_n}$

$(証明)$

　
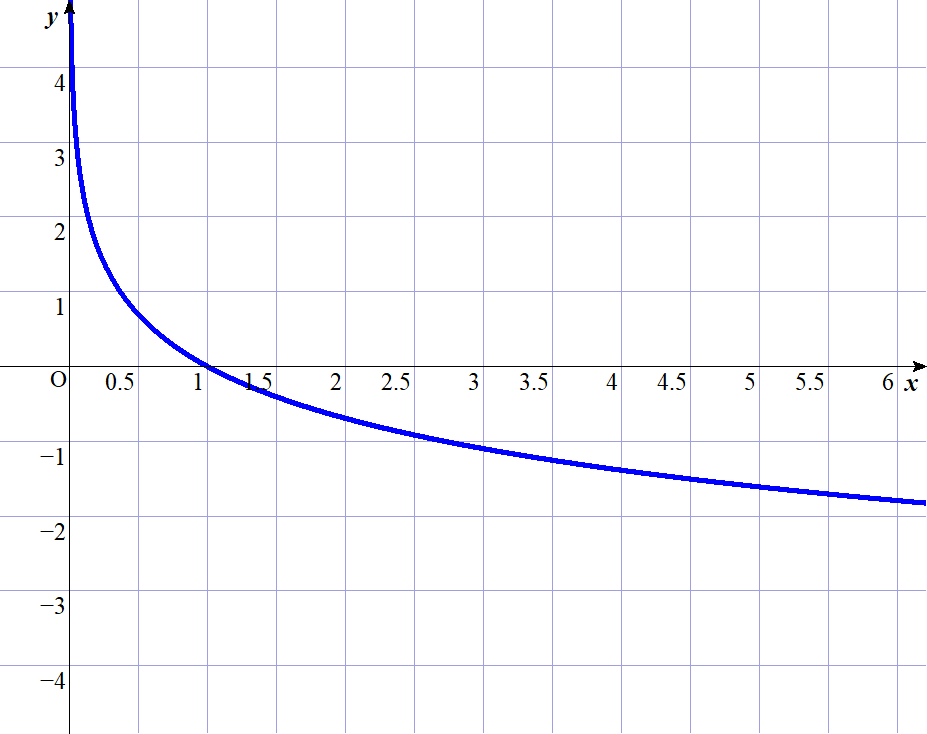
$f(x)=-\log{x}\ は \ x \geqq 0\ で凸関数だから$

$\qquad \alpha _1f(x_1)+\alpha _2f(x_2)+\cdots +\alpha _nf(x_n) \geqq f(\alpha _1x_1+\alpha _2 x_2+ \cdots +\alpha _n x_n)$

$したがって$

$\alpha _1(-\log{x_1})+\alpha _2(-\log{x_2}) +\cdots +\alpha _n(-\log{x_n})\geqq -\log{(\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n)}$

$\therefore \ \ \log{(\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n)} \geqq \alpha _1 \log{x_1} +\alpha _2 \log{x_2} +\cdots +\alpha _n \log{x_n} $

$($i$)の直接証明$

$\ \ m,\ \ n,\ a,\ b \ \ が正数で、m+n=1 \ \ のとき \quad \log{(ma+nb)} \geqq m\log{a}+n\log{b} \ \ を示します。$

$g(x)=nx-a^mx^n+ma \ \ を考える。$

$\quad g'(x)=n-na^mx^{n-1}=n(1-a^mx^{n-1})=n(1-a^mx^{-m})$

$g'(x)=0 \ \ より \quad x^m=a^m \quad \therefore \ \ x=a$

$g''(x)=mna^mx^{-m-1} \ \ より \quad g''(a)=mna^ma^{-m-1}=\cfrac{mn}{a} >0$

$よって \quad g(x)\ は \ x=a\ で極小値 \ \ g(a)=na-a^ma^n+ma=(m+n)a-a^{m+n}=a-a=0 \ \ をとる。$

$\therefore \ \ g(x)=nx-a^mx^n+ma \geqq 0 \quad x=b \ \ とおくと \quad ma + nb \geqq a^mb^n$

$\quad \therefore \ \ \log(ma+nb) \geqq \log a^mb^n =m\log a +n\log b$


$例3 \quad 三角関数$

(i)$\ \ \alpha _1,\ \alpha _2 \ が正数で、0 \leqq x_1 \leqq \pi , \ \ 0 \leqq x_2 \leqq \pi ,\ \ \alpha _1+\alpha _2=1 \ \ のとき$

$\hspace{3em} \sin{(\alpha _1 x_1+\alpha _2 x_2)} \geqq \alpha _1\sin{x_1}+\alpha _2\sin{x_2}$

(ii)$\ \ \alpha _1,\ \alpha _2,\ \cdots ,\ \alpha _n \ が正数で、0 \leqq x_1 \leqq \pi ,\ \ 0 \leqq x_2 \leqq \pi ,\ \cdots ,$

$\qquad 0 \leqq x_n \leqq \pi ,\ \ \alpha _1+\alpha _2 +\cdots +\alpha _n=1 \ \ のとき$

$\hspace{3em} \sin{(\alpha _1 x_1+\alpha _2 x_2+\cdots + \alpha _n x_n)} \geqq \alpha _1\sin{x_1}+\alpha _2\sin{x_2}+ \cdots +\alpha _n\sin{x_n}$

$(証明)$

　
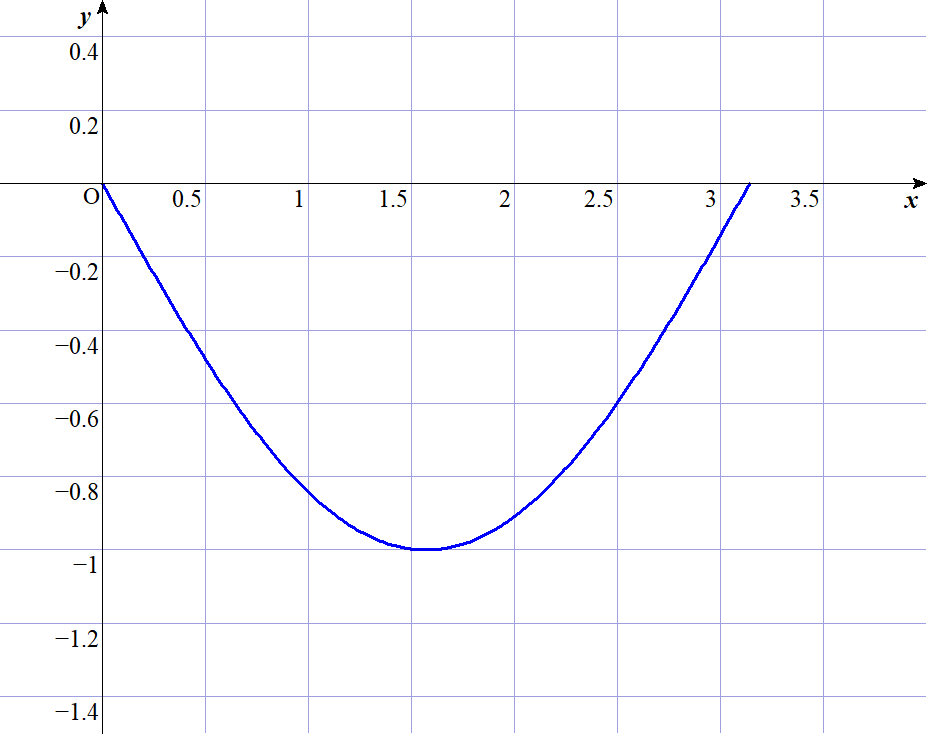
$f(x)=-\sin{x} \ \ は \ \ 0 \leqq x \leqq \pi \ \ で凸関数だから$

$\qquad \alpha _1f(x_1)+\alpha _2f(x_2)+\cdots +\alpha _nf(x_n) \geqq f(\alpha _1x_1+\alpha _2 x_2+ \cdots +\alpha _n x_n)$

$したがって$

$\alpha _1(-\sin{x_1})+\alpha _2(-\sin{x_2}) +\cdots +\alpha _n(-\sin{x_n}) \geqq -\sin{(\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n)}$

$\therefore \ \ \sin{(\alpha _1 x_1+\alpha _2 x_2 +\cdots + \alpha _n x_n)} \geqq \alpha _1 \sin{x_1} +\alpha _2 \sin{x_2} +\cdots +\alpha _n \sin{x_n} $


$($i$)の直接証明$

$\ \ m,\ n,\ a,\ b \ \ が正数で、m+n=1 \ \ のとき \quad \sin{(ma+nb)} \geqq m\sin{a}+n\sin{b} \ \ を示します。$

$g(x)=\sin (nx+ma)-n\sin x -m\sin a \quad を考える。$

$\quad g'(x)=n\cos (nx +ma)-n\cos x$

$\quad g''(x)=-n^2\sin (nx +ma)+n\sin x$

$\quad g'(x)=0 \ \ より \ \ \cos (nx +ma)=\cos x$

$\quad 0 < ma+nb < \pi \ \ だから \quad 0 < nx+ma <\pi \ \ よって \quad nx+ma=x \ \ より \quad x=\cfrac{ma}{1-n}=\cfrac{ma}{m}=a$
\begin{eqnarray*} g''(a) &=&-n^2\sin (na+ma)+n\sin a\\ \\ &=&-n^2\sin a+n\sin a\\ \\ &=&n(1-n)\sin a\\ \\ &=&nm\sin a\\ \end{eqnarray*} $n >0,\ \ m >0,\ \ 0 < a <\pi \ \ より \quad g''(a) >0$

$よって \ \ g(x)\ は\ x=a \ で極小となり、極小値は$
\begin{eqnarray*} g(a) &=&\sin(n+m)a -n\sin a -m\sin a\\ \\ &=&\sin a -(m+n)\sin a\\ \\ &=&\sin a-\sin a\\ \\ &=&0\\ \end{eqnarray*} $g(x) \geqq 0 \ \ より \quad \sin (nx+ma) \geqq n\sin x +m\sin a $

$x=b \ \ とおくと \quad \sin{(ma+nb)} \geqq m\sin{a}+n\sin{b}$


　

ページの先頭へ↑