東京都立大学(理系) 2024年 問題1
$以下の問いに答えなさい。ただし、\log \ は自然対数とする。$
$(1)\ \ 関数 \ f(x)=\cfrac{\log x}{x^2}\ \ (x > 0 )\ \ の増減を調べなさい。また、そのグラフの変曲点を求めなさい。$
\[(2)\ \ 3\ 以上の整数 \ n\ に対して、積分 \ \ \int_2^n \cfrac{\log x}{x^2}dx \ \ の値を求めなさい。\]
$(3)\ \ 3\ 以上の整数 \ n\ に対して、次の不等式が成り立つことを示しなさい。$
\[ \qquad \sum _{k=3}^n \cfrac{\log k}{k^2} < \cfrac{1}{2}(1+\log 2) \quad ただし、自然対数の底\ e\ が \ \ 2< e < 3\ \ をみたすことを用いてよい。\]
(1)
$f(x)=\cfrac{\log x}{x^2}\ \ より$
$f'(x)=\cfrac{\dfrac{1}{x} \times x^2 - \log x \times (2x)}{x^4}=\cfrac{1-2\log x}{x^3}$
$f''(x)=-\cfrac{\dfrac{2}{x} \times x^3 - (1-2\log x )\times (3x^2)}{x^6}=\cfrac{-2-3(1-2\log x}{x^4}=\cfrac{-5+6\log x}{x^4}$
$f'(x)=0 \quad より \quad \log x=\cfrac{1}{2} \qquad x=e^{\scriptsize{\dfrac{1}{2}}}$
$f''(x)=0 \quad より \quad \log x=\cfrac{5}{6} \qquad x=e^{\scriptsize{\dfrac{5}{6}}}$
$増減表は$
\[ \begin{array}{c||c|c|c|c|c} x & 0 & \cdots & e^{\scriptsize{\dfrac{1}{2}}} & \cdots & e^{\scriptsize{\dfrac{5}{6}}}\\ \hline f'(x) & & + & 0 & - & - & - \\ \hline f''(x) & & - & - & - & 0 & + \\ \hline f(x) & & \nearrow & 極大 & \searrow & 変曲点 & \searrow \\ & & 上に凸 & & 上に凸 & & 下に凸 \\ \end{array} \]
$f(x)\ は \ \ x = e^{\scriptsize{\dfrac{1}{2}}}\ \ で極大となり、$
$極大値は、f( e^{\scriptsize{\dfrac{1}{2}}})=\cfrac{1}{2e}$
$変曲点 \ A\ は、x = e^{\scriptsize{\dfrac{5}{6}}}\ \ のときで、$
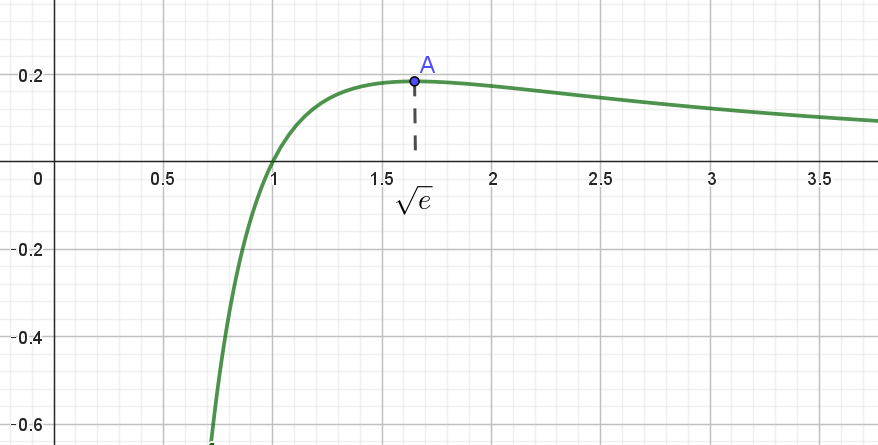
$f( e^{\scriptsize{\dfrac{5}{6}}})=\cfrac{5}{6e^{\scriptsize{\dfrac{5}{3}}}}=\dfrac{5}{6}e^{-\scriptsize{\dfrac{5}{3}}}$
$よって \quad A(e^{\scriptsize{\dfrac{5}{6}}}, \ \dfrac{5}{6}e^{-\scriptsize{\dfrac{5}{3}}})$
$x\ 軸を切る点は、\log x=0 \quad より \quad x=1$
$x \longrightarrow +0 \quad のとき \quad f(x) \longrightarrow -\infty$
$x \longrightarrow + \infty \quad のとき \quad f(x) \longrightarrow 0$
$このことについては($不定形の極限値(1)$)を参考にしてください。$
$よって \ \ x\ 軸,\ \ y\ 軸は漸近線で、グラフは右のとおり$
(2)
\begin{eqnarray*} & &\int_2^n \cfrac{\log x}{x^2}dx\\ \\ &=&\big[-\cfrac{1}{x}\log x \big]_2^n - \int_2^n \big(-\cfrac{1}{x}\big) \times \cfrac{1}{x} dx\\ \\ &=&-\cfrac{1}{n}\log n + \cfrac{1}{2} \log 2 + \int_2^n \cfrac{dx}{x^2}\\ \\ &=&-\cfrac{1}{n}\log n + \cfrac{1}{2} \log 2 + \big[-\cfrac{1}{x}\big]_2^n\\ \\ &=&-\cfrac{1}{n}\log n + \cfrac{1}{2} \log 2 - \cfrac{1}{n} + \cfrac{1}{2}\\ \\ &=&\cfrac{1}{2}(1+ \log 2) - \cfrac{1}{n}(1+\log n) \end{eqnarray*}(3)
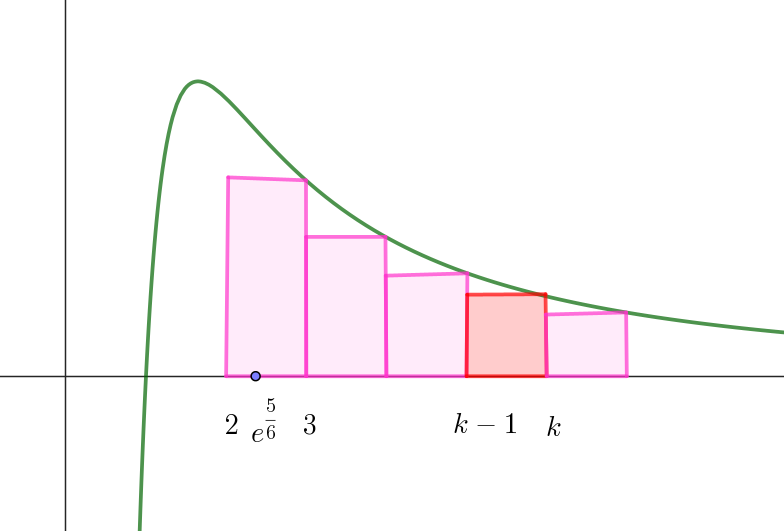
$y=f(x)\ \ の変曲点の \ x\ 座標について$
$e^{\scriptsize{\dfrac{5}{6}}} < e < 3 \quad だから$
$y=f(x)\ のグラフは \ \ x \geqq 3 \ \ で下に凸で$
$単調減少である。$
$したがって \ \ k=3,\ 4,\ \cdots \ \ について$
$右図のような幅 \ 1\ の長方形を考えることによって$
\[\cfrac{\log k}{k^2} < \int_{k-1}^k \cfrac{\log x}{x^2}dx \]
$和をとって$
\[\sum _{k=3}^n \cfrac{\log k}{k^2} < \sum_{k=3}^n \int_{k-1}^k \cfrac{\log x}{x^2}dx=\int_2^n \cfrac{\log x}{x^2}dx=\cfrac{1}{2}(1+ \log 2) - \cfrac{1}{n}(1+\log n)\]
$n \geqq 3 \quad のとき \quad \log n \geqq \log 3 >1 \quad だから \quad \cfrac{1}{n}(1+\log n) > 0$
\[よって、\sum _{k=3}^n \cfrac{\log k}{k^2} < \cfrac{1}{2}(1+ \log 2) \]
$(補充)$
\[\sum _{k=3}^n \cfrac{\log k}{k^2} \quad は上に有界で、単調に増加するから収束して和をもつことがわかりましたが、\]
$このことについては($正項級数$)を参考にしてください。$
メインメニュー に戻る