t分布
1 t分布
$自由度(1,n)のF分布の確率密度関数は$
\begin{eqnarray*} f_{1,n}(x) &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \Gamma(\dfrac{1}{2}) \Gamma(\dfrac{n}{2}) }\bigl(\cfrac{1}{n}\bigr)^{\small{\dfrac{1}{2} } } x^{ -\small{\dfrac{1}{2} } } (1+\dfrac{1}{n}x )^{ -\small{\dfrac{1+n}{2} }} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) }n^{-\small{\dfrac{1}{2} } } x^{ -\small{\dfrac{1}{2} } } (1+\dfrac{1}{n}x )^{ -\small{\dfrac{1+n}{2} }} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) }n^{-\small{\dfrac{1}{2} } }n^{\small{\dfrac{n+1}{2} } } x^{ -\small{\dfrac{1}{2} } } (x+n)^{ -\small{\dfrac{1+n}{2} }} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) } \cfrac{n^{\small{\dfrac{n}{2}}} }{x^{\small{\dfrac{1}{2} } }(x+n)^{ \small{\dfrac{1+n}{2} }}} \\ \end{eqnarray*} $x=t^2 \ \ と変数変換すると \ \ dx=2tdt \ \ より 確率変数Tのしたがう分布の確率密度関数 \ f_n(t) \ は$
$\quad f_{1,n}(x)dx=2f_n(t)dt=2f_n(t) \times \cfrac{dx}{2t}$
$したがって$
\begin{eqnarray*} f_n(t) &=&\sqrt{x}f_{1,n}(x)\\ &=&\sqrt{x} \times \cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) } \cfrac{n^{\small{\dfrac{n}{2}}} }{x^{\small{\dfrac{1}{2} } }(x+n)^{ \small{\dfrac{1+n}{2} }}} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) } \cfrac{n^{\small{\dfrac{n}{2}}} }{(x+n)^{ \small{\dfrac{1+n}{2} }}} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) } \cfrac{n^{\small{\dfrac{n}{2}}} }{ n^{\small{\dfrac{1+n}{2}}}\bigl(1+\cfrac{t^2}{n}\bigr)^{ \small{\dfrac{1+n}{2} }}} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi} \Gamma(\dfrac{n}{2}) } \cfrac{1}{ \sqrt{n}\bigl(1+\cfrac{t^2}{n}\bigr)^{ \small{\dfrac{1+n}{2} }}} \\ \\ &=&\cfrac{ \Gamma(\dfrac{1+n}{2}) } { \sqrt{\pi n} \Gamma(\dfrac{n}{2}) } \bigl(1+\cfrac{t^2}{n}\bigr)^{ -\small{\dfrac{1+n}{2} }} \\ \end{eqnarray*}
 $この密度関数をもつ分布を自由度nのt分布$
$この密度関数をもつ分布を自由度nのt分布$
$(スチューデント分布)といいますが、$
$本質的には自由度(1,n)のF分布のことです。$
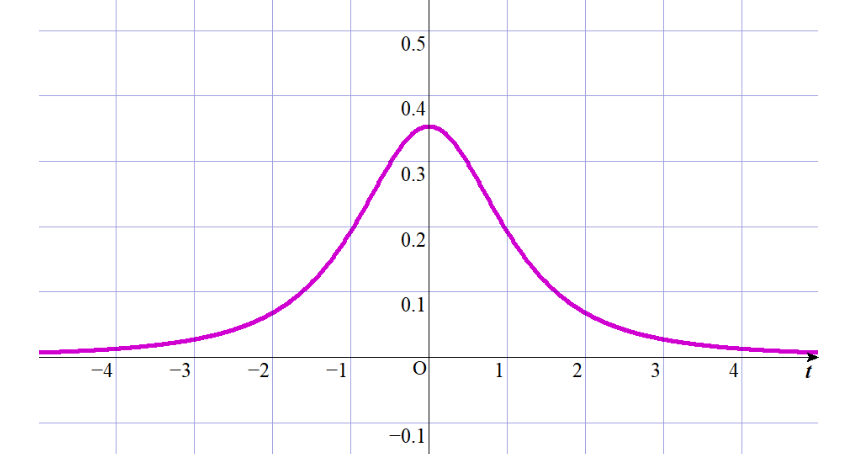
$偶関数ですから、グラフは直線 \ t=0 \ (縦軸)に$
$ついて対称です。$
$右図はn=2のt分布のグラフです。$
2 t分布にしたがう統計量
$定理$
$正規母集団 \ N(\mu,\ \sigma^2) \ からとった大きさnの標本 \ X_1,X_2, \cdots ,X_n について$
$\quad \cfrac{\sqrt{n-1}(\overline{X}-\mu)}{S} \ \ は自由度 \ n-1 \ のt分布にしたがう。$
$(証明)$
$\quad \cfrac{{(n-1)}(\overline{X}-\mu)^2}{S^2} \ \ は自由度 \ (1,n-1) \ のF分布にしたがうので、\quad ($F分布定理2$を参照してください)$
$\quad \cfrac{\sqrt{n-1}(\overline{X}-\mu)}{S} \ \ は自由度 \ n-1 \ のt分布にしたがう。$
$この定理により、母分散\sigma が未知の場合でも標本平均と標本分散を用いて、母平均\mu を区間推定したり、$
$検定することができます。$
メインメニュー に戻る