n個の集合の和集合の要素の個数
ここで扱う集合はすべて要素の個数が有限な有限集合とします。
(1) 3つの集合の和集合の要素の個数
高校の数学Ⅰあるいは数学Aで、2つの集合A,Bの和集合の要素の個数について
$\hspace{3em} n(A \cup B)=n(A)+n(B)-n(A \cap B)$
が成りたつことを学びます。
3つの集合A,B,Cの和集合の要素の個数について
$\qquad n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)$
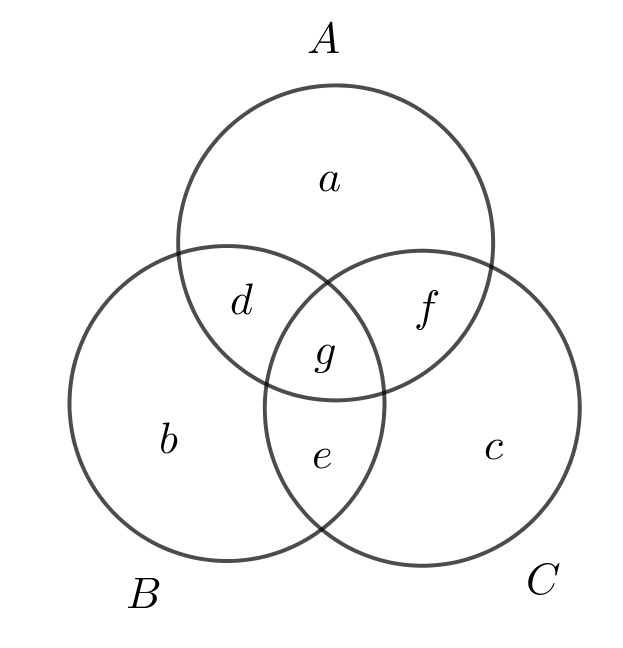
一応記述されており、その説明は右図を使って
$n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)$
$\hspace{2em} -n(C \cap A)+n(A \cap B \cap C)$
$=(a+d+g+f)+(b+d+g+e)+(c+e+f+g)$
$\hspace{2em} -(d+g)-(e+g)-(f+g)+g$
$=a+b+c+d+e+f+g$
$=n(A \cup B \cup C)$
と導いています。
この説明はわかりやすいが、なぜ1行目のような式を考えるかが天下り的です。
そこで集合が4個の場合でも拡張できるような説明を考えました。
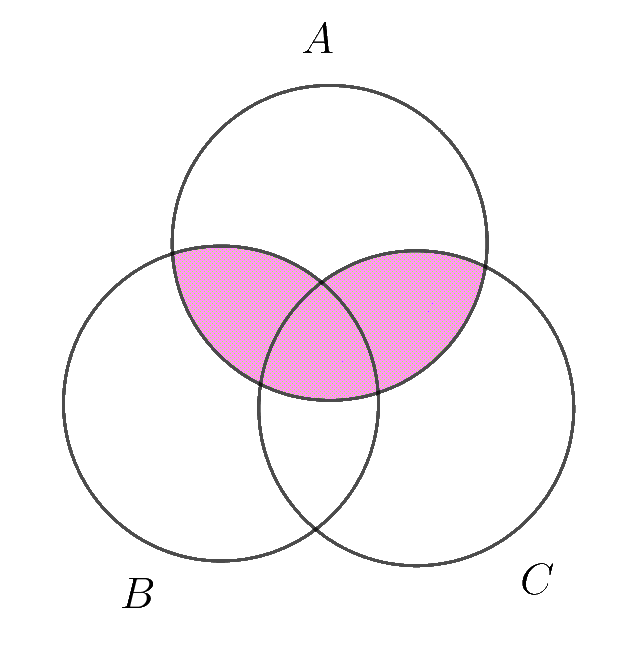
$\hspace{2em} A \cap (B \cup C)=(A \cap B) \cup (A \cap C)$
が必要ですが、高校では扱っていないので、まずこれを説明します。
法則の左辺、右辺とも右図の同じ部分であるから確かに等式が成りたちます。
2つの集合A,Bの和集合の要素の個数を求める式
$\hspace{2em} n(A \cup B)=n(A)+n(B)-n(A \cap B) $
$で、B \rightarrow B \cup C と置き換えると$
$\hspace{2em} n(A \cup B \cup C)$ \begin{eqnarray*} &=&n(A)+n(B \cup C)-n(A \cap (B \cup C))\\ &=&n(A)+n(B)+n(C)-n(B \cap C)-n((A \cap B)\cup (A \cap C))\\ &=&n(A)+n(B)+n(C)-n(B \cap C)-n(A \cap B)-n(A \cap C)+n((A \cap B)\cap (A \cap C))\\ &=&n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)\\ \end{eqnarray*}
となって、うまく導かれました。
(2) 4つの集合の和集合の要素の個数
4つの集合図はたとえば下図のようになります。

$2 \quad B$
$3 \quad C$
$4 \quad D$
$5 \quad A\cap B$
$6 \quad A\cap C$
$7 \quad A\cap D$
$8 \quad B\cap C$
$9 \quad B\cap D$
$10 \quad C\cap D$
$11 \quad A\cap B\cap C$
$12 \quad A\cap B\cap D$
$13 \quad A\cap C\cap D$
$14 \quad B\cap C\cap D$
$15 \quad A\cap B\cap C \cap D$
$16 \quad \overline{A\cup B\cup C \cup D}$
$ ここからは、集合Aの要素の個数を|A|と表すことにします。$
$ 3つの集合A,B,Cの和集合の要素の個数の関係式$
$\hspace{2em} |A \cup B \cup C |=|A|+|B|+|C|-|A \cap B|-|B \cap C|-|C \cap A|+|A \cap B \cap C|$
において、$C \rightarrow C \cup D とおくと$
$|A \cup B \cup C \cup D|$ $=|A|+|B|+|C\cup D|-|A \cap B|-|B \cap (C\cup D)|-|(C\cup D)\cap A|+|(A\cap B)\cap(C\cup D)|$
\begin{eqnarray*} 第5項&=&|(B\cap C)\cup (B\cap D)|\\ &=&|B\cap C|+|B\cap D|-|(B \cap C) \cap (B \cap D)|\\ &=&|B\cap C|+|B\cap D|-|B \cap C \cap D|\\ \end{eqnarray*}
\begin{eqnarray*} 第6項&=&|A\cap (C \cup D)|\\ &=&|(A\cap C)|\cup (A\cap D|\\ &=&|A\cap C|+|A\cap D|-|(A \cap C) \cap (A \cap D)|\\ &=&|A\cap C|+|A\cap D|-|A \cap C \cap D|\\ \end{eqnarray*}
\begin{eqnarray*} 第7項&=&|(A\cap B)\cap (C \cup D)|\\ &=&|(A\cap B\cap C)\cup (A \cap B \cap D)|\\ &=&|A\cap B\cap C|+|A \cap B \cap D|-|(A\cap B\cap C)\cap (A \cap B \cap D)|\\ &=&|A\cap B\cap C|+|A \cap B \cap D|-|A\cap B\cap C \cap D|\\ \end{eqnarray*} よって
$\hspace{2em} 左辺=|A|+|B|+|C|+|D|-|C\cap D|-|A \cap B| -|B \cap C|-|B\cap D)|+|B\cap C\cap D|$
$\hspace{5em} -|A \cap C|-|A\cap D)|+|A\cap C\cap D| +|A\cap B\cap C|+|A \cap B \cap D|-|A\cap B\cap C \cap D|$
これで4つの集合の和集合の要素の個数を求める式が見つかりました。
$\hspace{2em} |A \cup B \cup C \cup D|$
$\hspace{1em}=|A|+|B|+|C|+|D|-|A\cap B|-|A \cap C|-|A \cap D|-|B\cap C| -|B\cap D|-|C \cap D|$
$\hspace{2em} +|A\cap B\cap C|+|A\cap B\cap D| +|A\cap C\cap D|+|B\cap C\cap D| -|A\cap B\cap C \cap D|$
折角苦労して公式を導いたので、問題を解きましょう。
問題 $1から210までの自然数で、210と互いに素である数はいくつあるか。$
$\hspace{2em} U=\{1,2,\cdots , 210\}$とする。
$\hspace{2em} 210=2 \times 3 \times 5 \times 7$であるから
$\hspace{2em} Uの要素で、2,3,5,7の倍数の集合をそれぞれA,B,C,Dとすると$
$\hspace{3em} |A|=\cfrac{210}{2}=105,\hspace{3em} |B|=\cfrac{210}{3}=70, \hspace{3em} |C|=\cfrac{210}{5}=42, \hspace{3em} |D|=\cfrac{210}{7}=30$
$\hspace{3em} |A\cap B|=\cfrac{210}{2\times 3}=35 , \hspace{3em} |A\cap C|=\cfrac{210}{2\times 5}=21, \hspace{3em} |A\cap D|=\cfrac{210}{2\times 7}=15$
$\hspace{3em} |B\cap C|=\cfrac{210}{3\times 5}=14 , \hspace{3em} |B\cap D|=\cfrac{210}{3\times 7}=10, \hspace{3em} |C\cap D|=\cfrac{210}{5\times 7}=6$
$\hspace{3em} |A\cap B \cap C|=\cfrac{210}{2\times 3 \times 5}=7 , \hspace{3em} |A\cap B \cap D|=\cfrac{210}{2\times 3 \times 7}=5$
$\hspace{3em} |A\cap C \cap D|=\cfrac{210}{2\times 5 \times 7}=3 , \hspace{3em} |B\cap C \cap D|=\cfrac{210}{3\times 5 \times 7}=2$
$\hspace{3em} |A\cap B \cap C \cap D|=\cfrac{210}{2\times 3 \times 5 \times 7}=1$
であるから
$\hspace{3em} |A \cup B \cup C \cup D|=105+70+42+30-35-21-15-14-10-6+7+5+3+2-1 =162$
$よって 210と共通の約数をもたない、互いに素である数の個数は 210-162=48 個$
ところで
$自然数 1,2,\cdots ,m\ のうちmと互いに素な数の個数を\varphi(m) で表し、オイラー関数といいました。$
(オイラーの定理(整数論) 参照)
そして、性質として
$\quad p,qが互いに異なる素数ならば \varphi(pq)=\varphi(p)\varphi(q)$
が成りたつことを導きましたので、この問題ではこれが使えます。
\begin{eqnarray*} \varphi(210)&=&\varphi(2 \times 3 \times 5 \times 7)\\ &=&\varphi(2)\times \varphi(3)\times \varphi(5)\times \varphi(7)\\ &=&1 \times 2 \times 4 \times 6\\ &=&48\\ \end{eqnarray*}
(3) n個の集合の和集合の要素の個数
$\hspace{2em} 3つの集合の場合と4つの集合の場合から類推できますが$
\[n個の集合A_1,A_2,\cdots , A_nの和集合 \bigcup_{i=1}^{n}{ A_i}の要素の個数は\] \[|\bigcup_{i=1}^{n}{ A_i}|=\sum _{i=1}^{n}|A_i|- \sum_{i < j}^{n}|A_i \cap A_j|+\sum_{i < j < k}^{n}|A_i \cap A_j \cap A_k|- \cdots +(-1)^{n-1}|A_1 \cap A_2 \cap \cdots \cap A_n|\]
証明は、上のような方法で数学的帰納法で示せますが、計算は大変です。
特性関数を定義するうまい方法もありますが、こちらは専門書にあたってください。
メインメニュー に戻る