オイラーの定理
1 オイラー関数とオイラーの定理
$自然数 1,2,\cdots ,m\ のうちmと互いに素な数の個数を\varphi(m) で表し、オイラー関数といいます。$
例えば
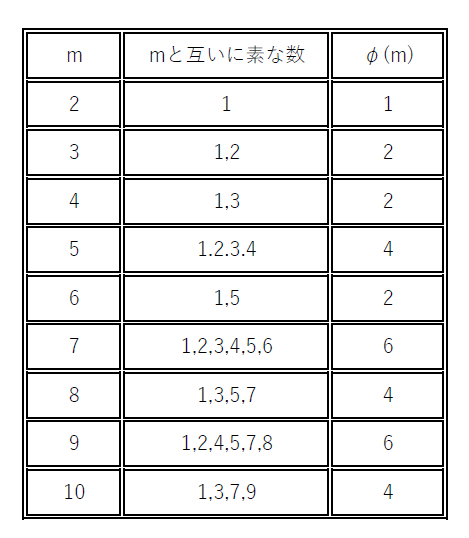
です。このオイラー関数を用いた定理が次のオイラーの定理です。
定理1 オイラーの定理
$\hspace{2em} a,mが互いに素な自然数のとき a^{\varphi(m)} \equiv 1\quad (mod \ \ m)$
(証明)
$1,2,\cdots,mのうち、mと互いに素な数は \varphi(m) 個あるからそれを\ r_1,r_2,\cdots ,r_l \ とする。$
$ただし l=\varphi(m) \ で r_i (i=1,2,\cdots , l)は異なるとする。$
$A=\{r_1,r_2,\cdots ,r_l \}$ とおく。
$また、mと互いに素な自然数aに対し、mを法として$
$\qquad ar_1 \equiv r_1',\ ar_2 \equiv r_2',\ \cdots ,\ ar_l \equiv r_l' \ とし B=\{r_1',\ r_2',\ \cdots ,\ r_l'\} \ とおく。$
(i)$\ B$の要素はすべて異なる。
もし $r_i' \equiv r_j' \ とすると$
$ar_i \equiv ar_j$
$a(r_i-r_j) \equiv 0$
$a とm は互いに素だから r_i \equiv r_j$
これはAの要素が異なることに矛盾する。
よって $r_i' \not\equiv r_j'$
(ii)$\ r_i' とm は互いに素$
$r_i' とm は互いに素でないとすると それらの最大公約数\ d\ は \ d >1$
$\qquad ar_i \equiv r_i' \ より ar_i =r_i'+mk \quad (k は整数)$
$これより dはar_iの約数となるから、dはar_iとmの公約数となる。$
ところが
$a とm は互いに素,r_iとm も互いに素だから ar_iとmも互いに素である。$
したがって $ar_iとmの公約数であるdは\ d=1\ となり、矛盾する。$
$よって ar_i \equiv r_i' \ とmは互いに素となり、Bのすべての要素はmと互いに素になる。$
(i)(ii)$よりA=B\ がいえる。$
証明を続ける前に、上のことについて具体例で確認しましょう。
$a=5,m=12 \ $としましょう。
$1,2,\cdots , 12 のうちで12と互いに素であるものは$
$A=\{1,5,7,11\} です。$
$このAの各要素を5倍すると、法12で$
$1 \times 5=5$
$5 \times 5=25 \equiv 1$
$7 \times 5=35 \equiv 11$
$11 \times 5=55 \equiv 7$
だから $B=\{5,1,11,7\} となって A=B \ となります。$
証明を続けます。
$Bの要素をすべてかけ合わせると$
$ar_1 \times ar_2 \times \cdots \times ar_l \equiv r_1' \times r_2' \times \cdots \times r_l'$
$a^l\ r_1r_2\cdots r_l=r_1'r_2' \cdots r_l'$
$A=B だったから r_1r_2\cdots r_l=r_1'r_2' \cdots r_l'$
$\therefore \ a^l\ r_1r_2\cdots r_l=r_1r_2 \cdots r_l$
$r_1r_2\cdots r_l \ は\ m と互いに素だから a^l \equiv 1$
よって $a^{\varphi(m)} \equiv 1\ (mod \ \ m)$
上の例では $5^4 \equiv 1\ (mod \ \ 12) となります。$
とくに$mが素数pならば \varphi(p)=p-1\ $だから
$\hspace{2em} a^{\varphi(m)} \equiv 1\quad は a^{p-1} \equiv 1$
となりフェルマーの小定理そのものになりますから、オイラーの定理は
フェルマーの小定理を拡張したものといえます。
2 オイラー関数の性質
オイラーの定理を利用するには、オイラー関数 $\ \varphi(m) \ $の値を求めなくてはなりません。
$mが小さいときは、mと互いに素な数をすべて書き出して個数を数えればよいのですが、$
$mが大きいときは困難です。$
そこで、$\varphi(m)の値を求めるのに役立つ性質を2つあげます。$
$(1)\quad p,qが互いに異なる素数ならば \varphi(pq)=\varphi(p)\varphi(q)$
(証明)
$1,2,3,\cdots ,pq \ のうちで$
$\hspace{2em} pの倍数は p,2p,3p,\cdots ,qp\ の\ q個$
$\hspace{2em} qの倍数は q,2q,3q,\cdots ,pq\ の\ p個$
$p,qは異なる素数だからpqの約数は全部で\ p+q-1 個 \ (pq \ のみダブっている)$
$\therefore \varphi(pq)=pq-(p+q-1)=(p-1)(q-1)=\varphi(p)\varphi(q)$
例 $\varphi(15)=\varphi(3 \times 5)=\varphi(3)\varphi(5)=2 \times 4=8$
$(2)\quad pが素数、kが自然数ならば \varphi(p^k)=p^k(1-\cfrac{1}{p})$
(証明)
$1,2,3,\cdots ,p^k のうちで$
$pの倍数は p,2p,3p,\cdots ,p^{k-1}p\ の\ p^{k-1}個だから$
$\varphi(p^k)=p^k-p^{k-1}=p^k(1-\cfrac{1}{p})$
例1 $\varphi(9)=\varphi(3^2)=3^2(1-\cfrac{1}{3})=6$
例2 $\varphi(42)$
\begin{eqnarray*} &=&\varphi(2 \times 3 \times 7)\\ &=&\varphi(2)\varphi(3 \times 7) \quad (2と3 \times 7 は異なる素数)\\ &=&\varphi(2)\varphi(3)\varphi(7)\\ &=&1 \times 2 \times 6\\ &=&12\\ \end{eqnarray*}
メインメニュー に戻る