面積分
$点(u,\ v)\ が平面上の領域 \ D\ を動くとき、$
$曲面\ S:\boldsymbol{r}=\boldsymbol{r}(u,\ v)=(x(u,\ v),\ y(u,\ v),\ z(u,\ v))\ 上の点 \ P(x,\ y,\ z)$
$に対して定義された連続なスカラー関数を $
$\quad \phi(u,\ v)=\phi(x(u,\ v),\ y(u,\ v),\ z(u,\ v))\ \ とする。$
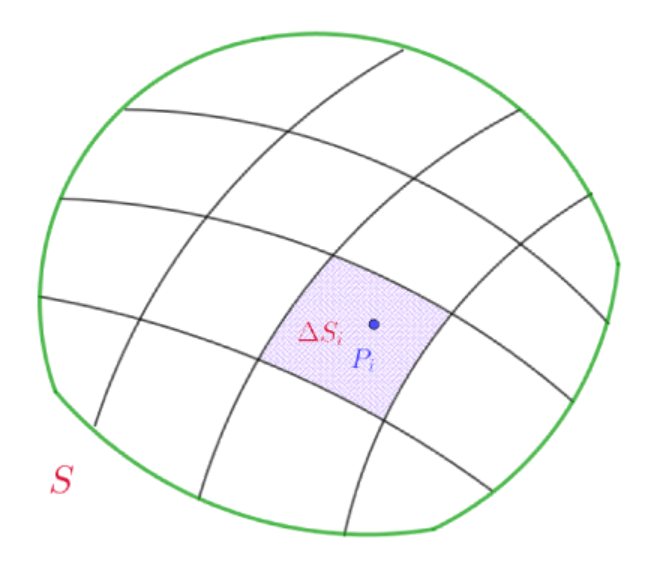
$S\ を \ S_1,\ S_2,\ \cdots ,\ S_n \ の \ n\ 個の微小曲面に分割することを分割 \ \Delta \ とする。$
$S_i\ の曲面積を \ \Delta S_i ,\ S_i\ の中に任意の点 \ P_i(x_i,\ y_i,\ z_i)\ をとり$
\[S(\Delta)=\sum_{i=1}^n \phi(x_i,y_i,z_i)\Delta S_i\]
$を考える。\quad n \longrightarrow \infty \quad として、分割を限りなく小さくしたとき \ S(\Delta) \ が極限値 \ S\ をもつならば$
\[S\ をスカラー場 \ \phi\ の面積分といい \quad \iint_S \phi dS \quad とあらわす。\]
$\quad dS=\big|\cfrac{\partial \boldsymbol{r}}{\partial u} \times \cfrac{\partial \boldsymbol{r}}{\partial v}\big| \ du dv
=\sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}dudv \quad だから$
$ \qquad この公式については($曲面積$)を参考にしてください。$
\[\iint_S \phi dS=\iint _D \phi(u,v) \sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}dudv\]
$\qquad とくに、\phi=1 \ \ のとき、この面積分は曲面 \ S\ の面積をあらわします。$$例1$
$曲面 \ \ \boldsymbol{r}=(\sin u \cos v,\ \sin u \sin v,\ \cos u)\ \ (0 \leqq u \leqq \cfrac{\pi}{2},\ \ 0 \leqq v \leqq 2\pi)\ \ 上のスカラー関数 \ \phi=x+y+z \ の面積分$
$\quad x^2+y^2+z^2=(\sin u \cos v)^2+(\sin u \sin v)^2+\ \cos ^2u=\sin ^2u+\cos ^2u=1$
$\quad だからこの曲面は 原点中心、半径 \ 1\ の球面です。$
$\qquad \cfrac{\partial (y,\ z)}{\partial (u,\ v)}=\cos u \sin v \times 0 - \sin u \cos v \times (-\sin u)=\sin ^2 u \cos v$
$\qquad \cfrac{\partial (z,\ x)}{\partial (u,\ v)}=-\sin u \times (-\sin u \sin v) - 0 \times \cos u \cos v=\sin ^2u \sin v$
$\qquad \cfrac{\partial (x,\ y)}{\partial (u,\ v)}=\cos u \cos v \times \sin u \cos v - (-\sin u \sin v) \times \cos u \sin v =\sin u \cos u \cos ^2v +\sin u \cos u \sin ^2v=\sin u \cos u$
\begin{eqnarray*} & &\sqrt{\big(\cfrac{\partial (y,\ z)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (z,\ x)}{\partial (u,\ v)}\big)^2 +\big(\cfrac{\partial (x,\ y)}{\partial (u,\ v)}\big)^2}\\ \\ &=&\sqrt{\sin ^4 u\cos ^2v +\sin ^4 u \sin ^2v + \sin ^2u \cos ^2u}\\ \\ &=&\sqrt{\sin ^4u +\sin ^2u\cos ^2u}\\ \\ &=&\sqrt{\sin ^2u(\sin ^2u+ \cos ^2u)}\\ \\ &=&\sin u \end{eqnarray*} $\phi(u,v)=\sin u \cos v+ \sin u \sin v + \cos u \quad だから$
\begin{eqnarray*} S &=&\iint_D (\sin u \cos v+ \sin u \sin v + \cos u)\sin u dudv\\ \\ &=& \int _0^{\scriptsize{\cfrac{\pi}{2}}} \int _0^{2\pi} (\sin ^2 u (\cos v+ \sin v) + \cos u \sin u dvdu\\ \\ &=& \int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin ^2 u du \int _0^{2\pi} (\cos v+ \sin v)dv + \int _0^{\scriptsize{\cfrac{\pi}{2}}} \cos u \sin u du \int _0^{2\pi}dv\\ \\ &=& \cfrac{1}{2}\int _0^{\scriptsize{\cfrac{\pi}{2}}} \sin 2u du \times 2\pi\\ \\ &=&\pi\big[-\cfrac{\cos 2u}{2}\big]_0^{\scriptsize{\cfrac{\pi}{2}}}\\ \\ &=&\pi \end{eqnarray*}
$曲面 \ S\ が \ \ z=z(x,\ y)\ \ と表されるとき \qquad dS=\sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}\ dxdy \ \ だから$
$ \qquad この公式については($曲面積$)を参考にしてください。$
\[\iint_S \phi dS=\iint _D \phi(x,y,z) \sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}\ dxdy\]
$例2$
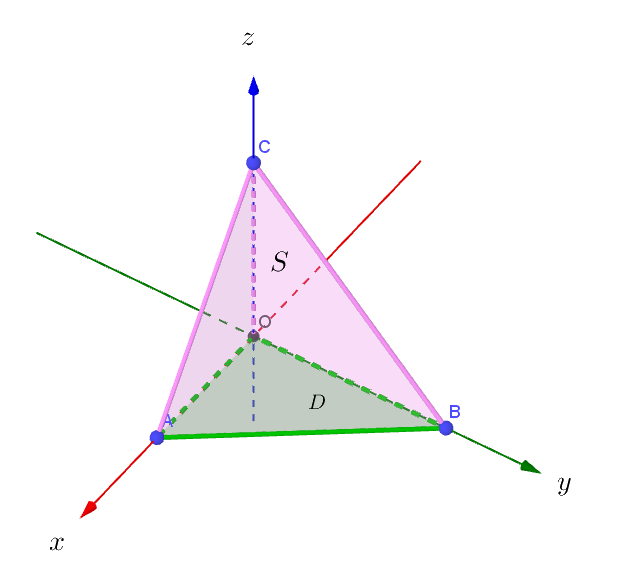
$平面 \ S: 2x+2y+z=2 \ \ (x \geqq 0,\ \ y \geqq 0,\ \ z \geqq 0)\ 上の$
$スカラー関数 \ \ \phi=x+y+z \ \ の面積分$
$z=2-2x-2y \quad より \quad \cfrac{\partial z}{\partial x} =-2,\qquad \cfrac{\partial z}{\partial y} =-2$
$\sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}=\sqrt{(-2)^2+(-2)^2+1}=3$
$z=2-2x-2y \geqq 0 \quad より \quad x+y \leqq 1$
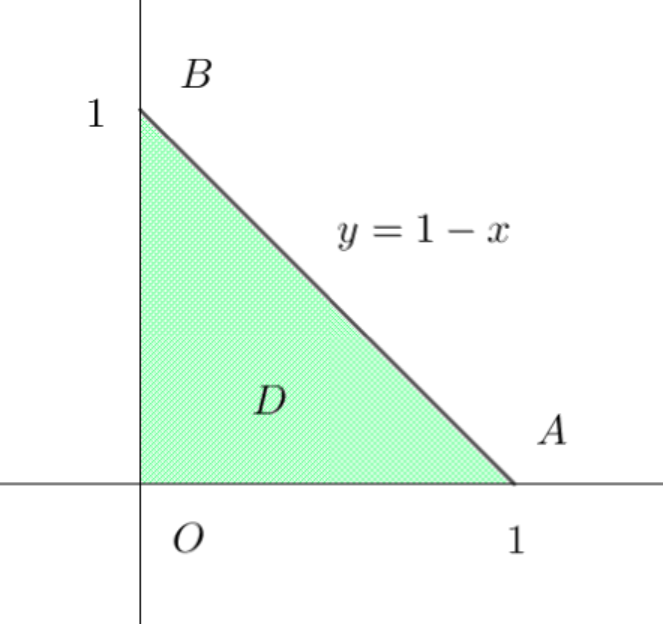
$\quad 0 \leqq y \leqq 1-x \quad だから \quad D=\{(x,\ y)\ |\ 0 \leqq x \leqq 1, \ \ 0 \leqq y \leqq 1-x\}$
$\quad \phi=x+y+(2-2x-2y)=-x-y+2$
\begin{eqnarray*}
S
&=&\iint _D \phi(x,y,z) \sqrt{(\cfrac{\partial z}{\partial x})^2+(\cfrac{\partial z}{\partial y})^2+1}\ dxdy\\
\\
&=&\iint _D (-x-y+2) \times 3dxdy\\
\\
&=&3\int _0^1 \int_0^{1-x} (-x-y+2) dydx\\
\\
&=&3\int _0^1 \big[(-x+2)y-\cfrac{y^2}{2}\big]_0^{1-x}dx\\
\\
&=&\cfrac{3}{2}\int _0^1 (x^2-4x+3)dx\\
\\
&=&2
\end{eqnarray*}
メインメニュー に戻る