斜回転による回転体の体積
$教科書ではx軸、あるいはy軸です。$
$直線 y=x \ は参考書に載っていますので、$
$ここでは、直線 l:y=ax+b \ を回転の軸$
$とした(これを斜回転といいます)曲線$
$ \ y=f(x)\ の回転体の体積を求めてみましょう。$
1 回転軸に垂直な平面でスライスする方法
$回転軸のある点からの距離 \ t\ をパラメータにとる方法が、オーソドックスな解法で、この方法による入試問題が$
$2024年岡山大学で出題されています。$2024岡山大学(理系)問題4$をご覧ください。$
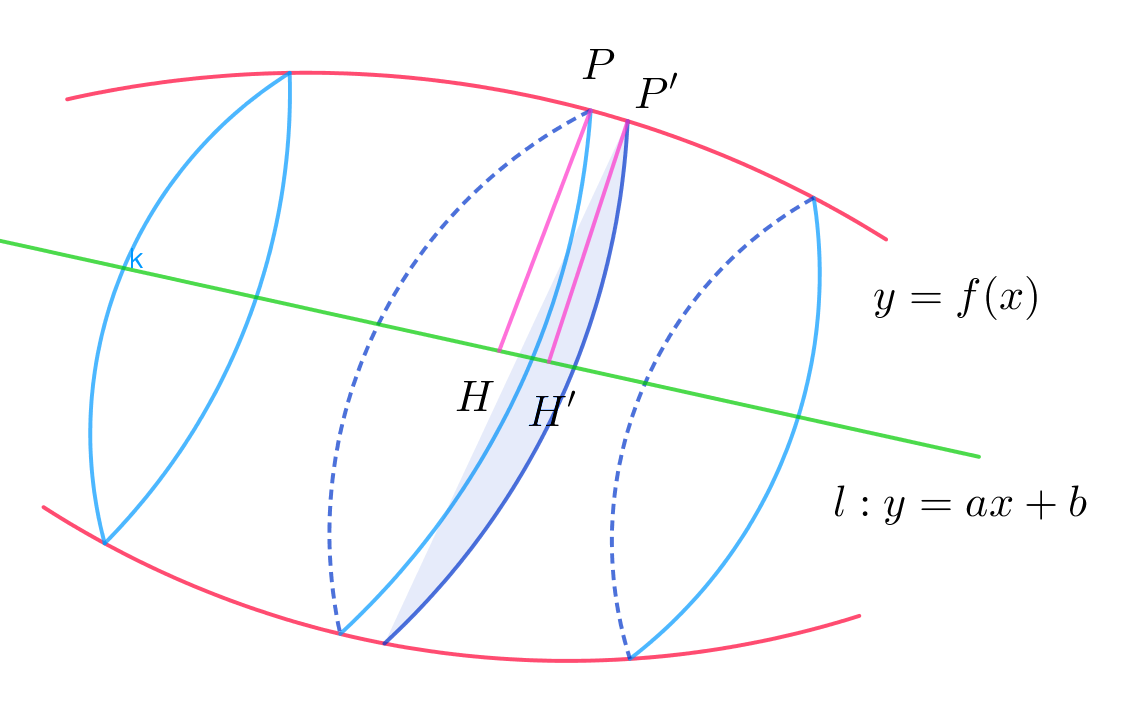
$(1)\ \ dx\ と \ dt\ の関係$
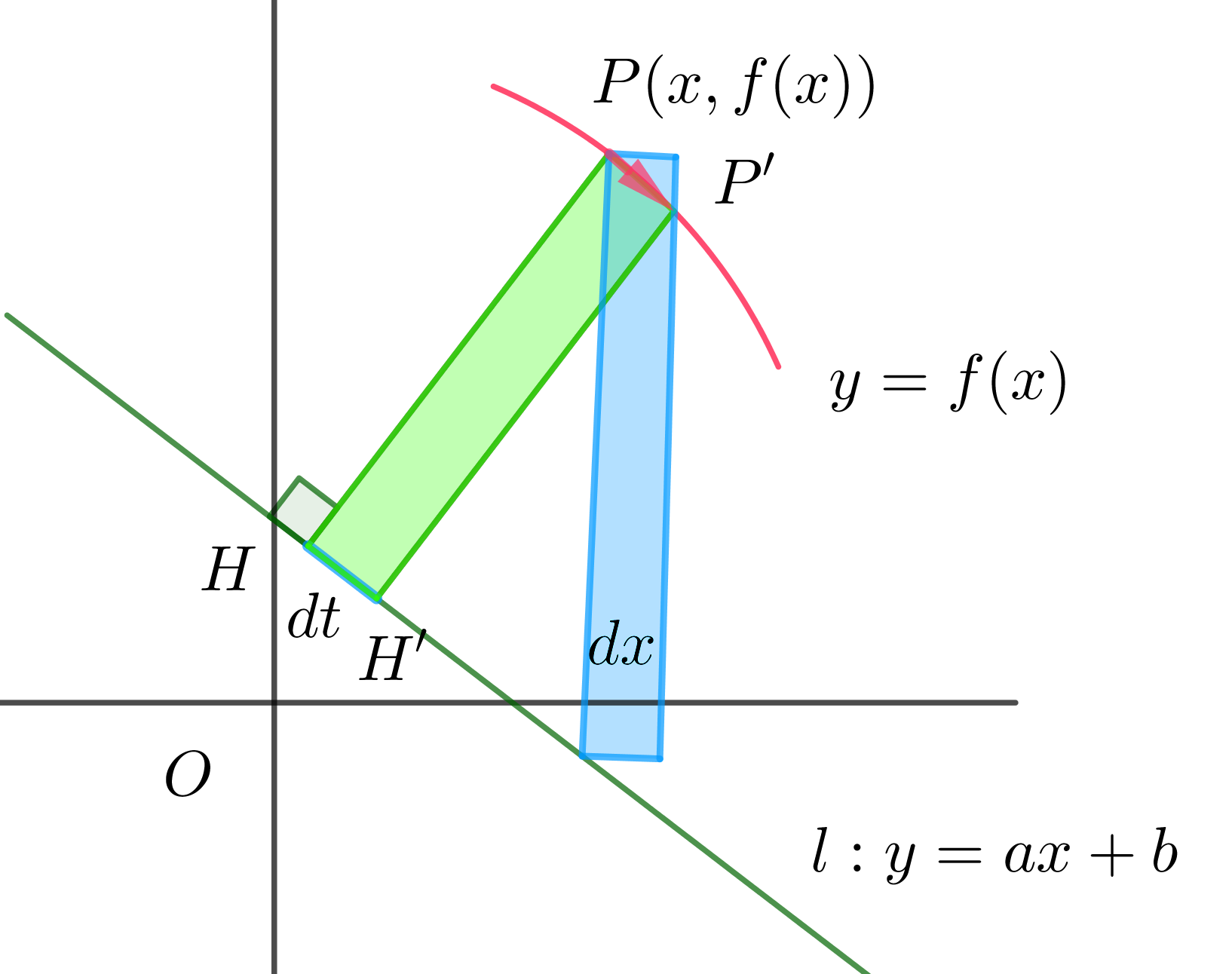
$曲線上の2点P(x,f(x))とP'(x+dx,f(x+dx))から$
$l\ に下ろした垂線の足をそれぞれH,H'とする。$
$このとき、x軸上の微小量dxに対応した直線 \ l\ 上の$
$微小量 \ dt=HH'\ は$
$\quad f(x+dx) \fallingdotseq f(x)+f'(x)dx だから$
$\quad \vec{PP'}=(x+dx,f(x)+f'(x)dx)-(x,f(x))=(dx,f'(x)dx)$
$直線\ l\ の方向ベクトルは \ (1,a)\ だから、単位ベクトルは \vec{u}=\cfrac{1}{\sqrt{1+a^2}}(1,a)$
$よって$
\begin{eqnarray*} dt&=&|\vec{HH'}|\\ &=&\vec{PP'}\cdot \vec{u}\\ &=&\cfrac{1}{\sqrt{1+a^2}} \big(dx+af'(x)\ dx\big)\\ \\ &=&\cfrac{1+af'(x)}{\sqrt{1+a^2}}\ dx\\ \end{eqnarray*}
$これが \ dx \ と \ dt\ の関係です。!!$
$当然x軸とt軸の分割の幅は異なりますし、dxが等分割であってもdtは一定になるとはかぎりません。$
$\quad dx\ と \ dt\ の関係 \hspace{2em} dt=\cfrac{1+af'(x)}{\sqrt{1+a^2}}dx$
$(2)\ \ 回転体の体積$
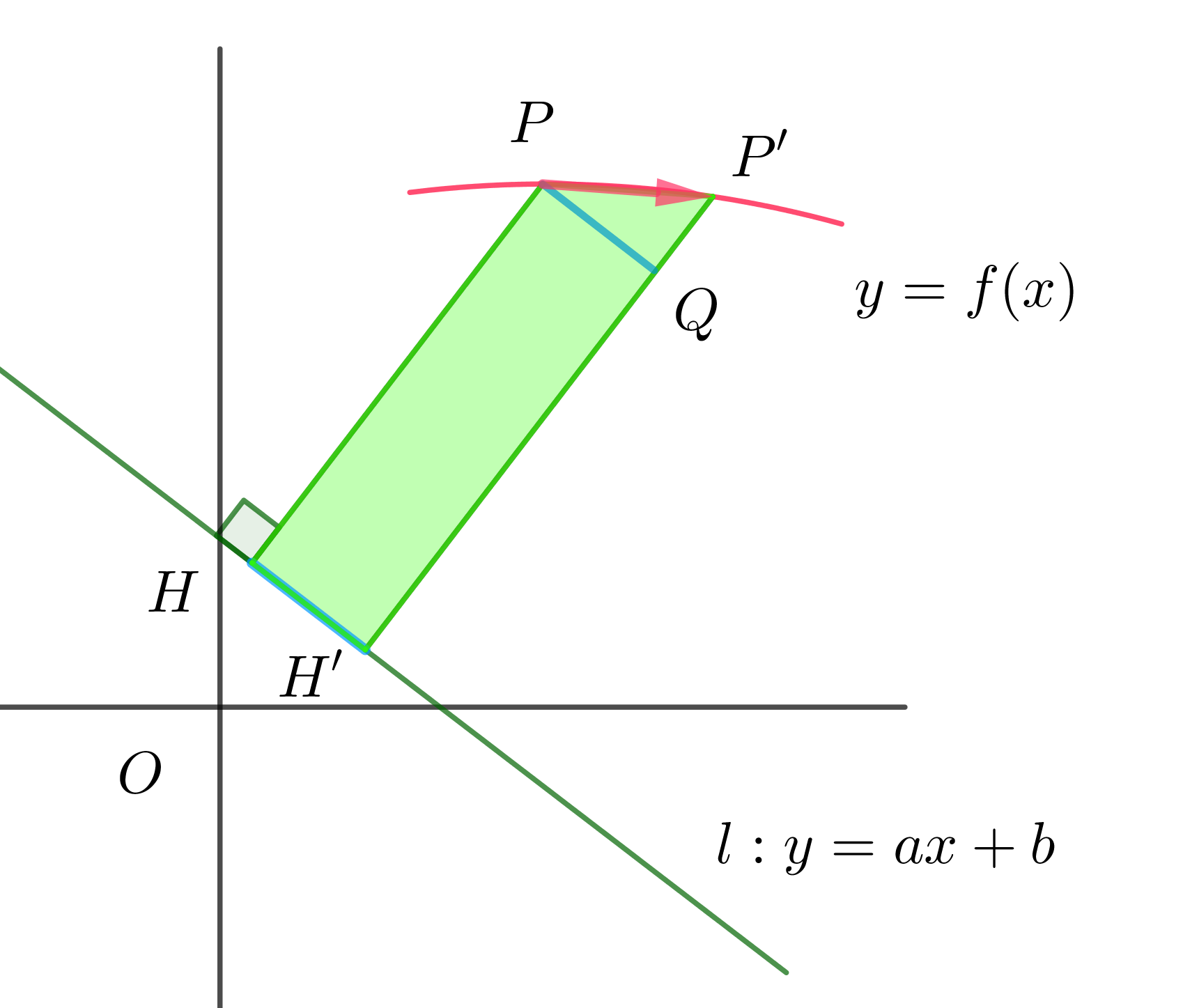
$\qquad PH=\cfrac{|ax-f(x)+b|}{\sqrt{1+a^2}}$
$直線P'H'上に \ PQ // HH' となるように点Qをとり、$
$(区分求積法の考え方です)長方形PHH'Q を直線 \ l\ の$
$まわりに一回転させると、回転体は円柱だから$
\begin{eqnarray*} dV&=&\pi\ PH^2\ HH'\\ &=&\pi\ \cfrac{\big(ax-f(x)+b\big)^2}{1+a^2}\ \cfrac{1+af'(x)}{\sqrt{1+a^2}}dx\\ &=&\cfrac{\pi}{\big(1+a^2\big)^{\dfrac{3}{2}}}\big(f(x)-ax-b\big)^2\big(1+af'(x)\big)dx\\ \end{eqnarray*}
$\quad 回転体の体積要素$
$\hspace{5em} dV=\cfrac{\pi}{\big(1+a^2\big)^{\dfrac{3}{2}}}\big(f(x)-ax-b\big)^2\big(1+af'(x)\big)dx$
$(3)\ \ 例題$
$放物線 y=-x^2+3 \ と直線 l\ :\ y=-x-3 \ で囲まれた領域をこの直線の回りに回転してできる$
$回転体の体積を求めてみましょう。$

$-x^2+3=-x-3 より x^2-x-6=0 \ を解いて$
$\qquad x=-2,\ 3$
$直線 y=-x-3 \ に垂直な直線が、放物線に接する$
$ときの接点Tの座標は、垂直な直線の傾きが \ 1\ だから$
$\quad y'=-2x=1\ より \ x=-\cfrac{1}{2} \ \ \therefore T(-\cfrac{1}{2},-\cfrac{5}{2})$
$放物線上の点P(x,f(x))とP'(x+dx,f(x+dx))から$
$直線 \ l\ に下ろした垂線の足をH,H'とすると$
$\quad \vec{PP'}=(dx,f'(x)dx)=(dx,-2xdx)$
$直線lの方向ベクトルは(1,-1)だから、単位ベクトルは \vec{u}=(\cfrac{1}{\sqrt{2}},-\cfrac{1}{\sqrt{2}})$
$\quad dt=|\vec{HH'}|=\vec{PP'}\cdot \vec{u}=(dx,-2xdx)\cdot (\cfrac{1}{\sqrt{2}},-\cfrac{1}{\sqrt{2}})=\cfrac{1+2x}{\sqrt{2}}dx$
$また PQ=(-x^2+3)-(-x-3)=-x^2+x+6 だから$
$\quad PH=\cfrac{PQ}{\sqrt{2}}=\cfrac{1}{\sqrt{2}}(-x^2+x+6)$
$直線P'H'上に \ PQ // HH' となるように点Qをとり、長方形PHH'Q を直線 \ l\ の$
$まわりに一回転させると、回転体は円柱だから$
\begin{eqnarray*} dV&=&\pi\ PH^2\ HH'\\ &=&\cfrac{\sqrt{2}\pi}{4}\ (-x^2+x+6)^2 \ (1+2x)dx\\ \end{eqnarray*}
$求める回転体の体積は、外側の放物線TRPの部分の回転体の体積V_1から、$
$内側の放物線TIの部分の回転体の体積V_2を引けばよいから$
\begin{eqnarray*} V&=&V_1-V_2\\ &=&\cfrac{\sqrt{2}\pi}{4}\int _{-\cfrac{1}{2}} ^3 (-x^2+x+6)^2 (2x+1)dx - \cfrac{\sqrt{2}\pi}{4}\int _{-\cfrac{1}{2}} ^{-2} (-x^2+x+6)^2 (2x+1)dx\\ &=&\cfrac{\sqrt{2}\pi}{4}\int _{-\cfrac{1}{2}} ^3 (-x^2+x+6)^2(2x+1)dx + \cfrac{\sqrt{2}\pi}{4}\int _{-2} ^{-\cfrac{1}{2}} (-x^2+x+6)^2(2x+1)dx\\ &=&\cfrac{\sqrt{2}\pi}{4}\int _{-2} ^3 (-x^2+x+6)^2(2x+1)dx\\ &=&\cfrac{\sqrt{2}\pi}{4}\int _{-2} ^3 (2x^5-3x^4-24x^3+13x^2+84x+36)dx\\ &=&\cfrac{625\sqrt{2}}{12}\pi\\ \end{eqnarray*}
2 傘型積分による方法
$このことについては($傘型積分による斜回転体の体積$)を参考にしてください。$
メインメニュー に戻る