傘型積分による斜回転体の体積

　

　$回転体の体積を求める際の回転軸は、$
$教科書ではx軸、あるいはy軸です。$
$直線 y=x \ は参考書に載っていますので、$
$ここでは、直線　l:y=ax+b \ を回転の軸$
$とした(これを斜回転といいます)曲線$
$ \ y=f(x)\ の回転体の体積を求めてみましょう。$


1　回転軸に垂直な平面でスライスする方法


$このことについては($斜回転による回転体の体積$)を参考にしてください。$


2　傘型積分による方法


$(1)\ \ 傘型積分とは$

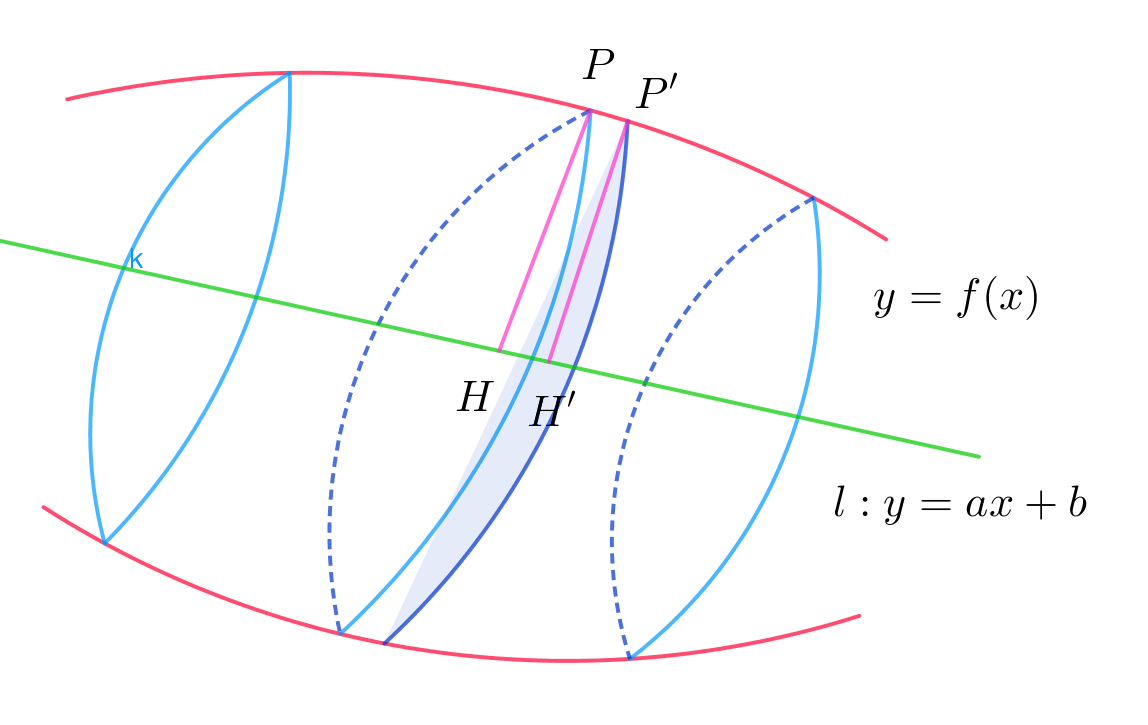
$図１のように、曲線 \ y=f(x) \ 上の点 \ P(x,f(x))\ を通りy軸に平行な直線が直線 \ l\ と交わる点を$
$\ Q(x,ax+b)\ とし、2点\ R(x+dx,ax+b),S(x+dx,f(x))\ をとって、長方形PQRSを考える。$

$\hspace{8em}$
$この長方形を直線 \ l\ のまわりに一回転させると、辺PS,QRの部分が影響してきれいな円錐にならない。$
$そこで、図２のように、この長方形と同じ面積の平行四辺形PQQ'P'を考える。$

　

$この平行四辺形PQQ'P'を直線lの周りに一回転$
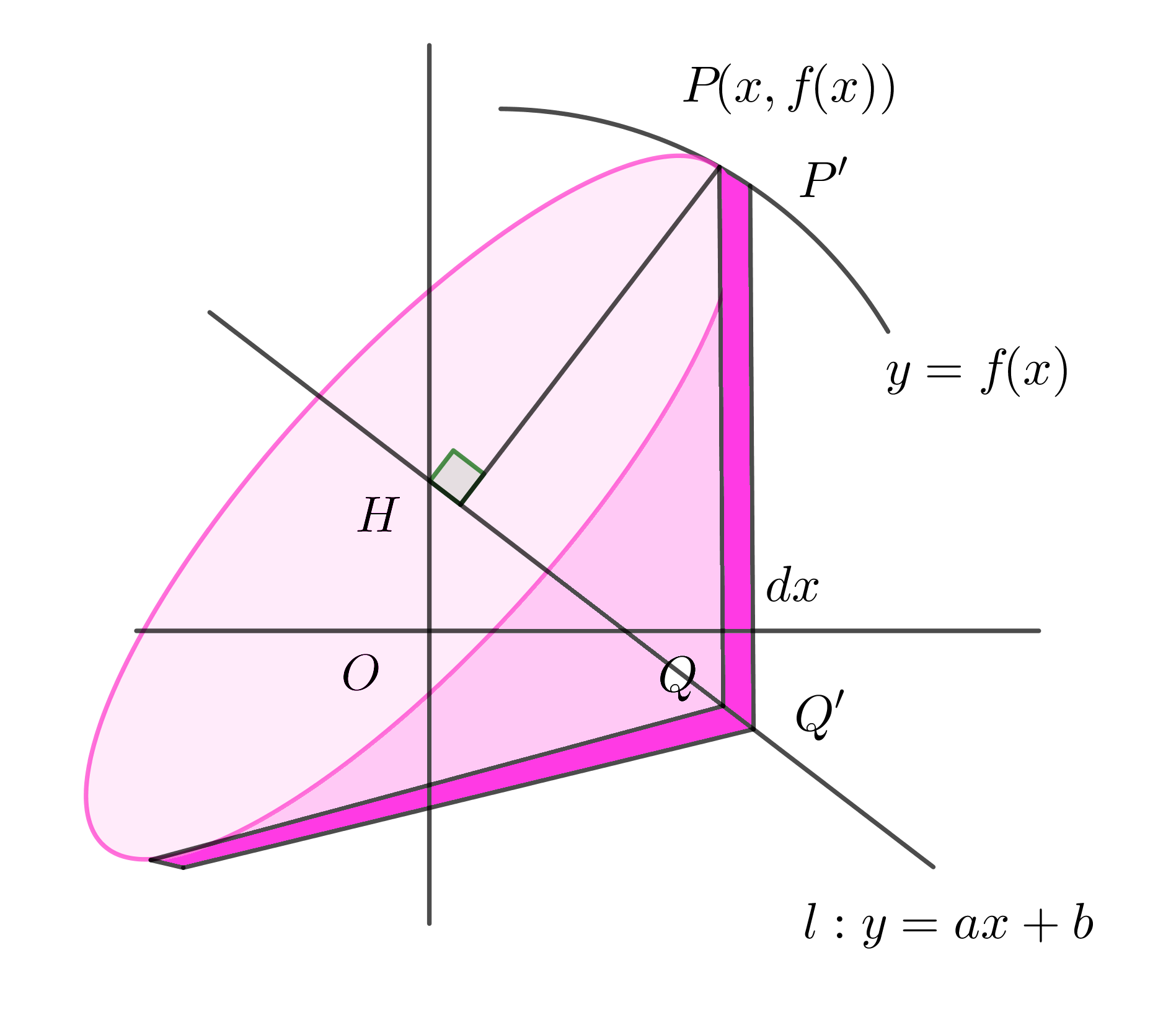
$させると傘のような立体（厚みのある円錐）が$
$得られる。$

$直線 \ l\ とx軸のなす角を\theta とすると$
$\tan \theta =a 　だから$
$\cos ^2 \theta =\cfrac{1}{1+\tan ^2 \theta }=\cfrac{1}{1+a^2}$

$\quad PH=PQ\cos \theta =\cfrac{PQ}{\sqrt{1+a^2}}$

$なお、右図では、\theta \ は鈍角で、\cos \theta < 0 \ \ ですから \ \ \cos \theta =-\cfrac{1}{\sqrt{1+a^2}}$
$したがって \quad PH=PQ\cos(\pi -\theta)=-PQ\cos \theta =\cfrac{PQ}{\sqrt{1+a^2}}$

$\quad 底面の円周は　l'=2\pi \ PH$
$\quad 円錐の側面積は$
\begin{eqnarray*} S&=&\pi PQ^2 \times \cfrac{l'}{2\pi PQ}\\ &=&\cfrac{1}{2}PQ \cdot l'\\ &=&\cfrac{1}{2}PQ \cdot 2\pi \ PH\\ &=&\pi PQ\cdot PH \\ &=&\cfrac{\pi PQ^2}{\sqrt{1+a^2}}\\ &=&\cfrac{\pi}{\sqrt{1+a^2}}\{f(x)-ax-b\}^2\\ \end{eqnarray*} $したがって　この円錐の微小体積dVは、厚みがdxであることに注意して$
$\quad dV=Sdx=\cfrac{\pi}{\sqrt{1+a^2}}\{f(x)-ax-b\}^2dx$

$この求め方を傘型積分といいます。少しわかりづらいのですが、この方法の優れている点は$
$被積分関数の次数が上がっていないことです。$

$\quad 傘型積分による回転体の体積要素$

$\hspace{5em} dV=\cfrac{\pi}{\sqrt{1+a^2}}\{f(x)-ax-b\}^2dx$



$(2)\ \ 傘型積分の解釈$

　

$平行四辺形PQQ'P'を直線 \ l\ の周りに一回転してできる$
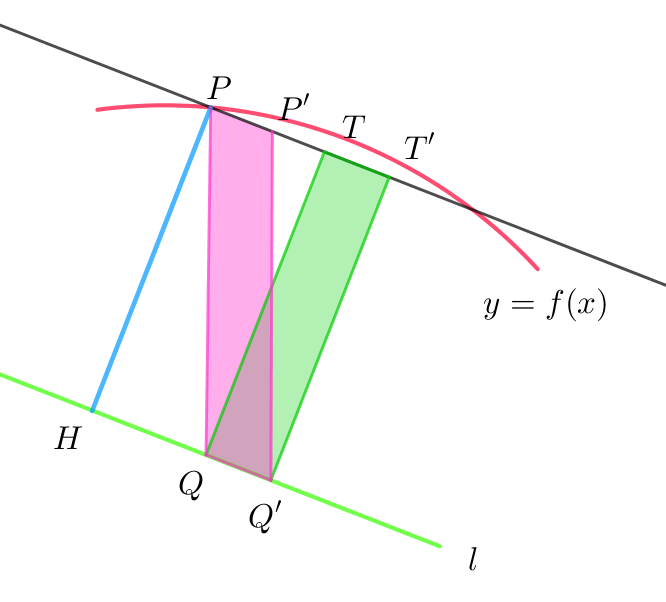
$立体(厚みのある円錐)の体積は、底辺と高さの等しい$
$長方形TQQ'T'を回転してできる円柱の体積に等しい。$
$すると$
$上の図1のx軸方向の線分PSと図2の直線 \ l\ に平行な$
$線分PP'の長さの関係は$

$\qquad PP'\cos \theta =PS 　だから$
$\qquad PP'=\cfrac{PS}{\cos \theta }=\cfrac{dx}{\cos \theta}$
$したがって$
\begin{eqnarray*} dV&=&\pi TQ^2\ QQ'\\ &=&\pi (PQ\cos \theta )^2\ PP'\\ &=&\pi PQ^2 \cos ^2\theta \times \cfrac{dx}{\cos \theta}\\ &=&\pi PQ^2 \cos \theta \ dx\\ &=&\cfrac{\pi PQ^2}{\sqrt{1+a^2}}\ dx\\ &=&\cfrac{\pi}{\sqrt{1+a^2}}\{f(x)-ax-b\}^2\ dx
\end{eqnarray*}
$となって、傘型積分の公式に一致しますが、これが傘型積分による求め方の本質です。$


$例題$

$放物線　y=-x^2+3\ と直線　y=-x-3\ で囲まれた領域をこの直線の回りに回転してできる$
$回転体の体積を傘型積分で計算してみましょう。$

　

$\quad a=1$
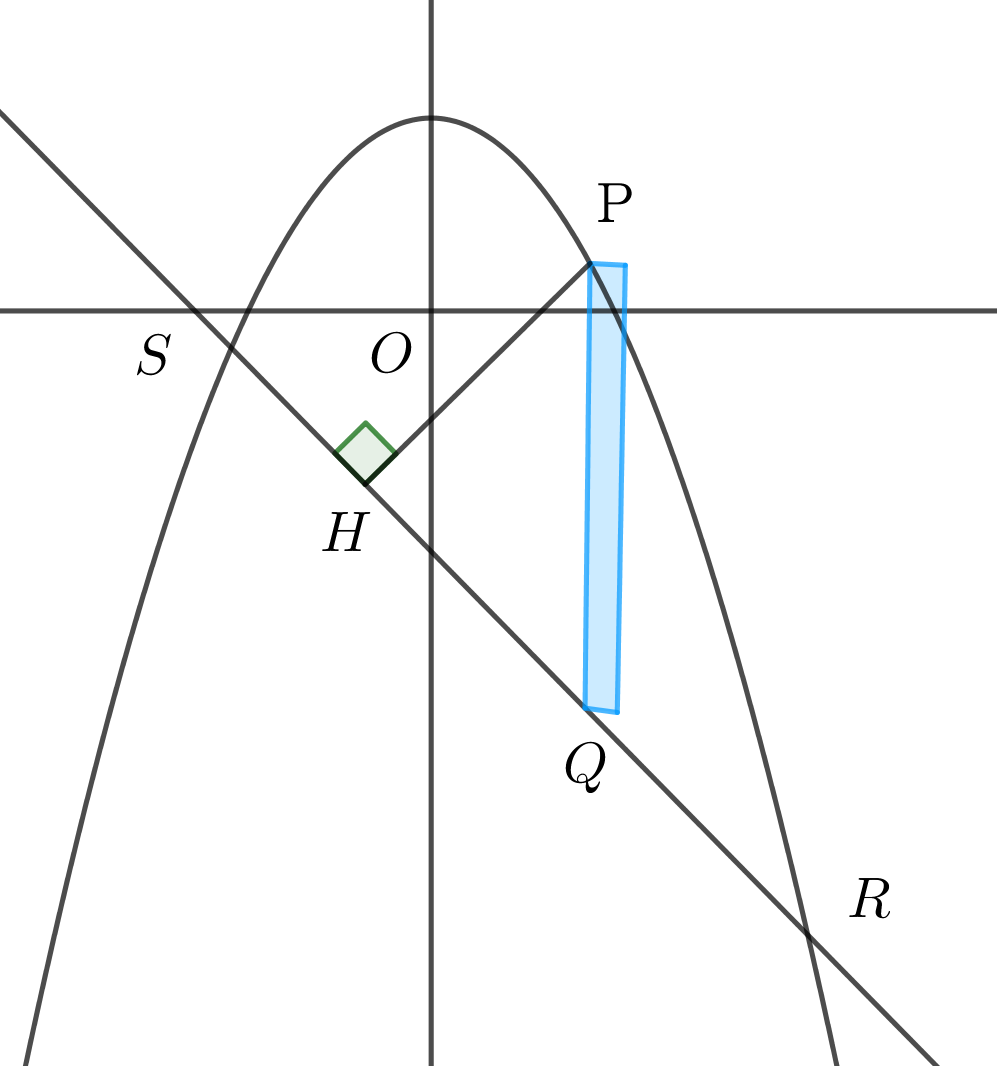
$\quad PQ=-x^2+3-(-x-3)=-x^2+x+6$

$したがって$

$\qquad dV=\cfrac{\pi}{\sqrt{2}}(-x^2+x+6)^2dx$
\begin{eqnarray*} V&=&\int _{-2} ^3 \cfrac{\pi}{\sqrt{2}}(-x^2+x+6)^2dx\\ &=&\cfrac{\sqrt{2}\pi}{2}\int _{-2} ^3 (x^4-2x^3-11x^2+12x+36)dx\\ &=&\cfrac{625\sqrt{2}}{12}\pi\\ \end{eqnarray*}
$積分計算がだいぶ楽になりました。$


$なお、被積分関数を$
\begin{eqnarray*} (-x^2+x+6)^2&=&(x+2)^2(x-3)^2\\ &=&(x-3+5)^2(x-3)^2\\ &=&\{(x-3)^2+10(x-3)+25\}(x-3)^2\\ &=&(x-3)^4+10(x-3)^3+25(x-3)^2\\ \end{eqnarray*} $と展開して積分する方法もあります。$


3　2つの求め方による回転体の体積が一致する理由


　

$曲線 \ y=f(x)\ と直線 \ l:y=ax+b\ の交点の$
$x座標を\ \alpha \ と \ \beta \quad (\alpha < \beta )\ \ とすると$
$\alpha \ と \ \beta \ は　f(x)-ax-b=0 \ の解であるから$

$\quad f(\alpha)-a\alpha -b=0 , \quad f(\beta)-a\beta -b=0$

$dV_1=\cfrac{\pi}{\big(1+a^2\big)^{\dfrac{3}{2}}}\big(f(x)-ax-b\big)^2\big(1+af'(x)\big)dx$

$dV_2=\cfrac{\pi}{\sqrt{1+a^2}}\big(f(x)-ax-b\big)^2dx$

$この2つの差をとると$

$\hspace{3em}dV_1-dV_2$
\begin{eqnarray*} &=&\cfrac{\pi}{\big(1+a^2\big)^{\dfrac{3}{2}}}\big(f(x)-ax-b\big)^2\big(1+af'(x)\big)dx- \cfrac{\pi}{\sqrt{1+a^2}}\big(f(x)-ax-b\big)^2dx\\ \\ &=&\cfrac{\pi}{\big(1+a^2\big)^{\dfrac{3}{2}}}(f(x)-ax-b)^2\{(1+af'(x)-(1+a^2)\}dx\\ \\ &=&\cfrac{\pi a}{\big(1+a^2\big)^{\dfrac{3}{2}}}(f(x)-ax-b)^2(f'(x)-a)dx\\ \end{eqnarray*}
$f'(x)-a\ の不定積分は \ f(x)-ax-b \ とおけることに注意して、部分積分を行うと$
\begin{eqnarray*} I&=&\int _{\alpha} ^{\beta} (f(x)-ax-b)^2(f'(x)-a)dx\\ \\ &=&\big[(f(x)-ax-b)^3\big] _{\alpha} ^{\beta} -2\int _{\alpha} ^{\beta} (f(x)-ax-b)^2(f'(x)-a)dx\\ \\ &=& -2\int _{\alpha} ^{\beta} (f(x)-ax-b)^2(f'(x)-a)dx\\ \\ &=&-2I\\ \end{eqnarray*} $\therefore I=0$

$したがって　V_1=V_2 \ となり、2つの求め方による回転体の体積は一致することがわかりました。$


$この証明方法がわからず、長い間不思議に感じていました。$
$もちろん参考書や専門書にも記述はありません。$
$つい最近、2018年の東北大学の入試問題を解いている中で、ふとアイデアが浮かびました$
$ので、この原稿を書きました。$
$気がつけば非常に簡単なことでした。!!!$




ページの先頭へ↑



メインメニュー　に戻る