最小偏差多項式
1 最小偏差多項式とは
$n次多項式f(x)について、a \leqq x \leqq b における|f(x)|の最大値をf(x)の偏差といい、$
$n次多項式の中で、この偏差を最小にする多項式を最小偏差多項式という。$
ポイントは
(1) 各次数の最小偏差多項式を具体的に求める。
(2) 最小偏差多項式の性質を調べる。
ということになります。
ちょっとわかりずらい定義ですので、具体例で考えましょう。
2 2次の最小偏差式
$\hspace{2em} T_2(x)=2x^2-1 の -1 \leqq x \leqq 1 における |T_2(x)|の最大値(偏差といいます)をMとします。$
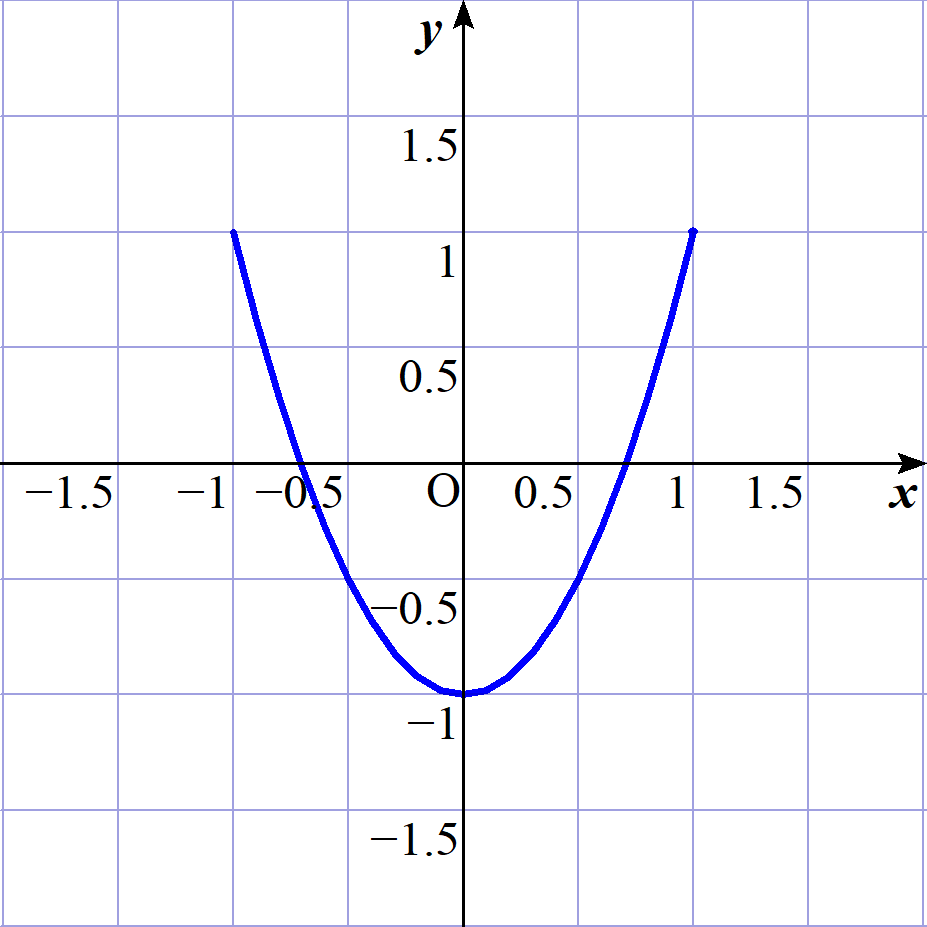
$(1) まずはこのM$を求めましょう。
$\hspace{2em} T_2(1)=1,\quad T_2(-1)=1$
$\hspace{2em} T_2(x)の最小値は T_2(0)=-1$
$\quad したがって \quad |T_2(x)|の最大値は$
$\hspace{2em} x=1,\ x=0,\ x=-1 のときで M=1$
$(2)\quad -1 \leqq x \leqq 1 において\quad |g(x)| < M\ である連続な関数 g(x) を考える。$
$\quad 方程式 g(x)-T_2(x)=0 は -1 < x < 1 で少なくとも2つの解をもつ。$
(証明)
$\quad (1) より M=1 だから |g(x)| < 1 よって -1 < g(x) < 1 $
$\quad したがって \quad -1 \leqq x \leqq 1 の任意のxに対して g(x)-1 < 0 , \quad g(x)+1 > 0$
$\quad F(x)=g(x)-T_2(x)$ とおくと
$\quad F(1)=g(1)-T_2(1)=g(1)-1 < 0$
$\quad F(0)=g(0)-T_2(0)=g(0)+1 > 0$
$\quad F(-1)=g(-1)-T_2(-1)=g(-1)-1 < 0$
$\quad F(x)は連続関数だから、中間値の定理より (0,1),(-1,0) の各区間で F(x)=0 $
$\quad となるx がそれぞれ少なくとも1個あるから、合計少なくとも2つの解を持つ。$
$(3) \quad g(x)=2x^2+ax+b の -1 \leqq x \leqq 1 における |g(x)|の最大値はM以上である。$
(証明)
$\quad 背理法で示す。$
$\quad (1) より M=1 だから |g(x)|の最大値が M より小さいとすると$
$\quad -1 \leqq x \leqq 1 であるすべてのx に対して |g(x)| < 1$
$\quad よって\quad -1 < g(x) < 1 \therefore g(x)-1 < 0 , \quad g(x) + 1 >0$
$\quad F(x)=g(x)-T_2(x) を考えると \quad F(x)=(2x^2+ax+b)-(2x^2-1)=ax+b+1$
$\quad (2)より\ \ F(x)=0 は -1 < x < 1 で少なくとも2個の解をもつが、F(x)=0 は$
$\quad 一次方程式だから高々1個の解しかもたない。これは矛盾である。$
$\quad したがって、 |g(x)|の最大値はM以上である。$
$(4) \quad |g(x)|の最大値がMとなるg(x)はT_2(x)以外ない。$
$\quad (3)より、max|g(x)| \geqq M であるから |g(x)| の最大値が最小となるものを求めることになる。$
$\quad そのような g(x)=2x^2+ax+b は$
$\hspace{2em} 端点で g(1)=1, \quad g(-1)=1$
$\hspace{2em} x= \alpha \quad (-1 < \alpha < 1) で 極小値 g(\alpha )=-1 \quad をとるから$
\[ \left\{ \begin{array}{l} g(1)=2+a+b=1 \hspace{30em}\\ g(-1)=2-a+b=0 \\ \end{array} \right. \] $\quad これを解いて a=0 , \ b=-1 よって g(x)=2x^2-1$
$\quad g(x) は確かに x=0 で極小値 \ -1 \ をとる。$
$\quad したがって g(x) \equiv T_2(x)$
3 3次の最小偏差式
$T_3(x)=4x^3-3x の -1 \leqq x \leqq 1 における |T_3(x)|\ の最大値(偏差)をMとします。$
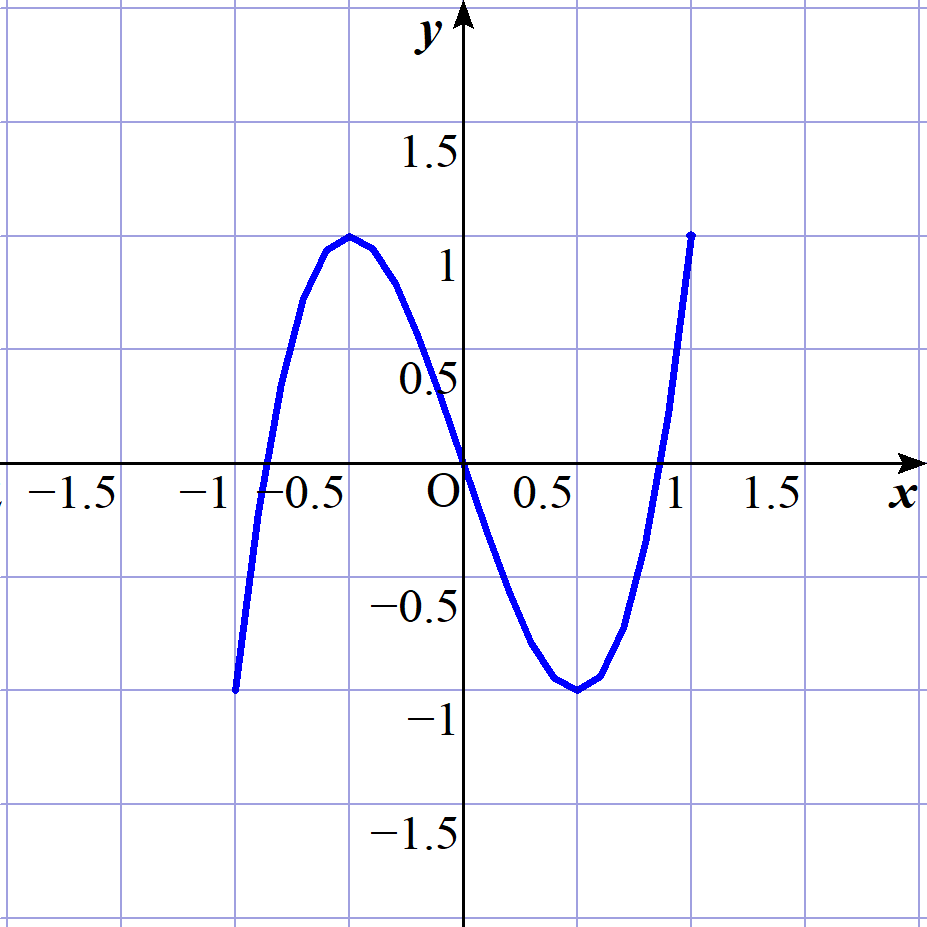
$(1) このM$を求めましょう。
$\quad T_3'(x)=12x^2-3=3(2x+1)(2x-1)$
\[ \begin{array}{|c||c|c|c|c|c|c|c|} \hline x&-1&\cdots&-\cfrac{1}{2}&\cdots&\cfrac{1}{2}&\cdots&1\\ \hline f'(x)& &+&0&-&0&+& \\ \hline f(x)& &\nearrow&極大&\searrow&極小&\nearrow& \\ \hline \end{array} \] $\quad T_3(1)=1,\ T_3(-1)=-1, \ T_3(\cfrac{1}{2})=-1,\ T_3(-\cfrac{1}{2})=1$
したがって
$\quad |T_3(x)| \ の最大値は x=1,\ x=\cfrac{1}{2},\ x=-\cfrac{1}{2},\ x=1 のときで M=1$
$(2)\quad -1 \leqq x \leqq 1 において |g(x)| < M である連続な関数 g(x) を考える。$
$\quad 方程式 g(x)-T_3(x)=0 は -1 < x < 1 で少なくとも3つの解をもつ。$
(証明)
$\quad (1) より M=1 だから |g(x)|<1 よって -1 < g(x) < 1$
$\quad したがって \quad -1 \leqq x \leqq 1 の任意の\ x\ に対して g(x)-1 < 0 , \quad g(x)+1 > 0$
$\quad そこで F(x)=g(x)-T_3(x) とおくと$
$\quad F(1)=g(1)-T_3(1)=g(1)-1 < 0$
$\quad F(\cfrac{1}{2})=g(\cfrac{1}{2})-T_3(\cfrac{1}{2})=g(\cfrac{1}{2})+1 > 0$
$\quad F(-\cfrac{1}{2})=g(-\cfrac{1}{2})-T_3(-\cfrac{1}{2})=g(-\cfrac{1}{2})-1 < 0$
$\quad F(-1)=g(-1)-T_3(-1)=g(-1)+1 > 0$
$\quad F(x)は連続関数だから、中間値の定理より (\cfrac{1}{2},1),\ (-\cfrac{1}{2},\cfrac{1}{2}),\ (-1,-\cfrac{1}{2}) の各区間で$
$\quad F(x)=0 となるx がそれぞれ少なくとも1個ずつあるから、合計少なくとも3つの解を持つ。$
$(3) \quad g(x)=4x^3+ax^2+bx+c の -1 \leqq x \leqq 1 における\ |g(x)|\ の最大値はM以上である。$
$\quad 背理法で示す$
$\quad (1) より M=1 だから |g(x)|の最大値が M より小さいとすると$
$\quad -1 \leqq x \leqq 1 \ であるすべてのx に対して |g(x)| < 1$
よって
$\quad -1 < g(x) < 1 \quad \therefore g(x)-1 < 0 , \quad g(x) + 1 > 0$
$\quad F(x)=g(x)-T_3(x) \ を考えると$
$\quad F(x)=(4x^3+ax^2+bx+c)-(4x^3-3x)=ax^2+(b+3)x+c$
$\quad (2)より F(x)=0 は -1 < x < 1 で少なくとも3個の解をもつ。$
$\quad F(x)=0 は二次方程式だから高々2個の解しかもたないからこれは矛盾である。$
$\quad したがって、 |g(x)|の最大値はM以上である。$
$(4) \quad g(x)=4x^3+ax^2+bx+c で |g(x)|の最大値がMとなるg(x)は \ T_3(x)以外ない。$
(証明)
$\quad (3)より、max|g(x)| \geqq M であるから |g(x)|$ の最大値が最小となるものを求めることになる。
$\quad そのような g(x) は、$
$\quad 端点で g(1)=1, \quad g(-1)=-1 $
$\quad x= \alpha で 極小値 -1 ,\quad x= \beta で 極大値 1 をとる。ただし、-1 < \beta < 0 < \alpha < 1$
$\quad g(-1)=-1,\ g(\alpha)=-1,\ g'(\alpha)=0 だから g(x)+1=4(x-\alpha)^2(x+1)$ とおける。
$\hspace{2em} x=1 を代入して 2=4(1-\alpha)^2 \times 2$
$\hspace{2em} 0 < \alpha <1 だから 1-\alpha=\cfrac{1}{2} \quad \therefore \alpha=\cfrac{1}{2}$
$よって \quad g(x)=4(x-\cfrac{1}{2})^2(x+1)-1=4x^3-3x$
$\hspace{2em} これは確かに、\beta =-\cfrac{1}{2} \ で極大値 \ 1\ をとる。$
$\hspace{2em} したがって g(x) \equiv T_3(x)$
4 4次の最小偏差式
$T_4(x)=8x^4-8x^2+1 の -1 \leqq x \leqq 1 における |T_4(x)|の最大値(偏差)をMとする。$
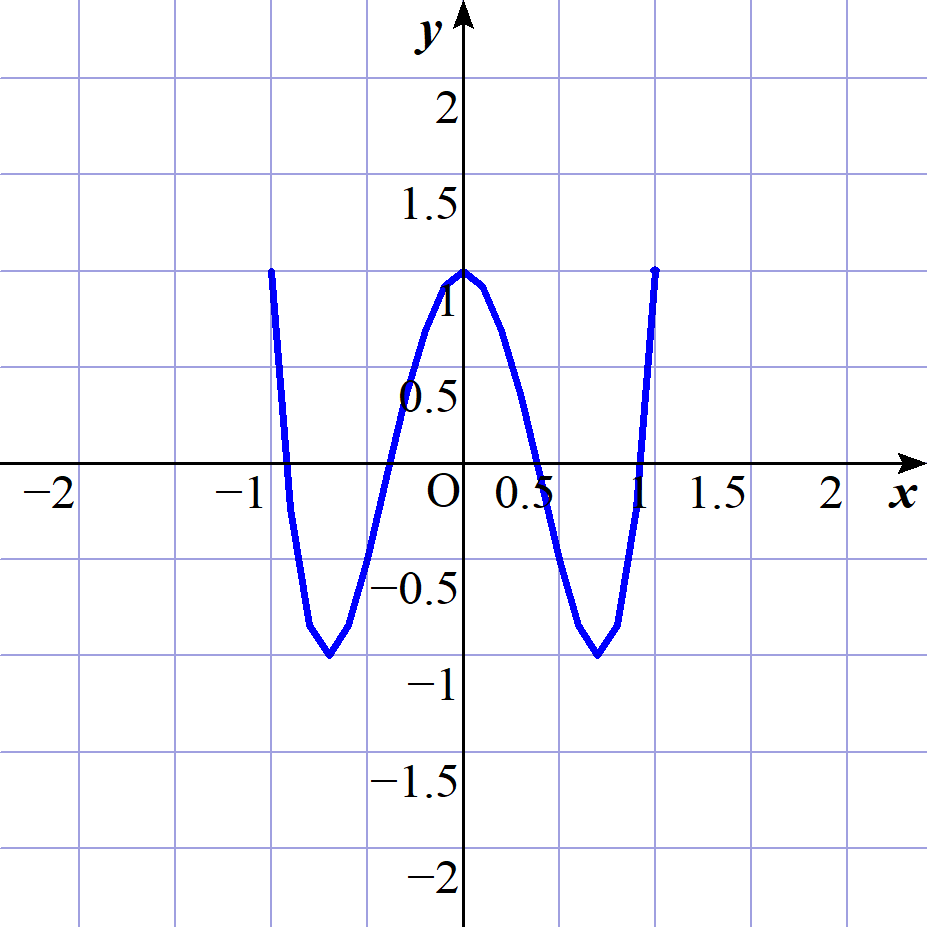
$(1) このM$を求めましょう。
$\quad T_4'(x)=32x^3-16x=16x(\sqrt{2}x+1)(\sqrt{2}x-1)$
\[ \begin{array}{|c||c|c|c|c|c|c|c|c|c|} \hline x&-1&\cdots&-\cfrac{1}{\sqrt{2}}&\cdots&0&\cdots&\cfrac{1}{\sqrt{2}}&\cdots&1\\ \hline f'(x)& &-&0&+&0&-&0&+& \\ \hline f(x)& &\searrow&極小&\nearrow&極大&\searrow&極小&\nearrow& \\ \hline \end{array} \]
$\quad T_4(1)=1,\ T_4(0)=1,\ T_4(-1)=1,\ T_4(\cfrac{1}{\sqrt{2}})=-1,\ T_4(-\cfrac{1}{\sqrt{2}})=-1$
$\quad したがって |T_4(x)|の最大値は$
$\quad x=1,\ x=\cfrac{1}{\sqrt{2}},\ x=0,x=-\cfrac{1}{\sqrt{2}},\ x=-1$ のときで $M=1$
$(2)\quad -1 \leqq x \leqq 1 において |g(x)| < M である連続な関数 g(x) を考える。$
$\quad 方程式 g(x)-T_4(x)=0 は -1 < x < 1 で少なくとも4つの解をもつ。$
(証明)
$\quad (1) より M=1 だから |g(x)|<1 よって -1 < g(x) < 1$
$\quad したがって \quad -1 \leqq x \leqq 1 の任意のxに対して g(x)-1 < 0 , \quad g(x)+1 > 0$
$\quad F(x)=g(x)-T_4(x) とおくと$
$\hspace{2em} F(1)=g(1)-T_4(1)=g(1)-1 < 0$
$\hspace{2em} F(\cfrac{1}{\sqrt{2}})=g(\cfrac{1}{\sqrt{2}})-T_4(\cfrac{1}{\sqrt{2}})=g(\cfrac{1}{\sqrt{2}})+1 > 0$
$\hspace{2em} F(0)=g(0)-T_4(0)=g(0)-1 < 0$
$\hspace{2em} F(-\cfrac{1}{\sqrt{2}})=g(-\cfrac{1}{\sqrt{2}})-T_4(-\cfrac{1}{\sqrt{2}})=g(-\cfrac{1}{\sqrt{2}})+1 > 0$
$\hspace{2em} F(-1)=g(-1)-T_4(-1)=g(-1)-1 < 0$
$\quad F(x)は連続関数だから、中間値の定理より$
$\hspace{2em} (\cfrac{1}{\sqrt{2}},1), \ (0,\cfrac{1}{\sqrt{2}}), \ (-\cfrac{1}{\sqrt{2}},0),\ (-1,-\cfrac{1}{\sqrt{2}}) の各区間でF(x)=0$
$\hspace{2em} となるxがそれぞれ少なくとも1個あるから、合計少なくとも4つの解を持つ。$
$(3) \quad g(x)=8x^4+ax^3+bx^2+cx+d の -1 \leqq x \leqq 1 における\ |g(x)|\ の最大値はM以上である。$
(証明)
背理法で示す。
$\quad (1) より M=1 だから |g(x)|の最大値が M より小さいとすると、$
$-1 \leqq x \leqq 1 であるすべてのx に対して |g(x)| < 1 $
$\quad よって -1 < g(x) < 1 \quad \therefore g(x)-1 < 0 , \quad g(x) + 1 >0$
$\quad F(x)=g(x)-T_4(x) を考える。$
$\quad F(x)=(8x^4+ax^3+bx^2+cx+d)-(8x^4-8x^2+1)$
$\quad \hspace{2em} =ax^3+(b+8)x^2+cx+d-1$
$\quad (2)より F(x)=0 は -1 < x < 1 で少なくとも4個の解をもつが、F(x)=0 は$
$\quad 三次方程式だから高々3個の解しかもたない。これは矛盾である。$
$\quad したがって、 |g(x)|の最大値は1以上である。$
$(4) \quad g(x)=8x^4+ax^3+bx^2+cx+d で |g(x)|の最大値がMとなる\ g(x)はT_4(x)以外ない。$
(証明)
$\quad (3)より、max|g(x)| \geqq M であるから |g(x)| の最大値が最小となるものを求めることになる。$
$\quad そのような g(x) は$
$\hspace{2em} 端点で g(1)=1, \ g(-1)=1 , \ 極大値 1, \ 極小値 -1 \ となるものである。$
$\quad そこで、x=\alpha で極大値、x=\beta , \gamma で極小値をとるとする。ただし、-1 < \gamma < \alpha < \beta < 1$
$\hspace{2em} g(\alpha)=1,\ g'(\alpha)=0,\ g(\beta)=-1,\ g'(\beta)=0,\ g(\gamma)=-1, g'(\gamma)=0$
$\quad よって\quad g(x)+1=8(x-\beta)^2(x-\gamma)^2 とおけるから$
$\quad x=1 を代入して$
$\hspace{2em} 2=8(1-\beta)^2(1-\gamma)^2$
$\hspace{2em} \therefore (1-\beta)(1-\gamma)=\cfrac{1}{2} \hspace{14em} (1)$
$\quad x=-1 を代入して$
$\hspace{2em} 2=8(-1-\beta)^2(-1-\gamma)^2$
$\hspace{2em} (1+\beta)(1+\gamma)=\cfrac{1}{2} \hspace{15em} (2)$
$\quad (1)(2) より \gamma=-\beta$
$\quad (1)に代入して$
$\quad (1-\beta)(1+\beta)=\cfrac{1}{2}$
$\quad \beta^2=\cfrac{1}{2}, \quad 0 < \beta < 1 だから \beta=\cfrac{1}{\sqrt{2}}$
$\quad よって \gamma=-\cfrac{1}{\sqrt{2}}$
したがって
\begin{eqnarray*} g(x) &=&8(x-\cfrac{1}{\sqrt{2}})^2(x+\cfrac{1}{\sqrt{2}})^2-1 \hspace{28em}\\ &=&8(x^2-\cfrac{1}{2})^2-1\\ &=&8x^4-8x^2+1\\ \end{eqnarray*}
$これは確かに x=0 で極小値をとるから、g(x) \equiv T_4(x)$
5 まとめ
$最小偏差多項式 \ T_n(x)\ (n=2,3,4) \ について$
$(1) \quad -1 \leqq x \leqq 1 において$
$\quad $(i)$\quad g(x)=2x^2+ax+b の偏差 \ M \ は M \geqq 1 で等号は T_2(x)=2x^2-1$
$\quad $(ii)$\quad g(x)=4x^3+ax^2+bx+c の偏差 \ M \ は M \geqq 1 で等号は T_3(x)=4x^3-3x$
$\quad $(iii)$\quad g(x)=8x^4+ax^3+bx^2+cx+d の偏差 \ M \ は M \geqq 1 で等号は \ \ T_4(x)=8x^4-8x^2+1$
$(2) 極値をとる点を 1>x_1>x_2>\cdots >-1 とすると$
$\hspace{3em} T_n(1)=1,\ T_n(x_1)=-1,\ T_n(x_2)=1,\ T_n(x_3)=-1 , \cdots と 1,\ -1 を交互にとる。$
6 最小偏差多項式の式の形
$\hspace{1em} 定理 \hspace{2em} -1 \leqq x \leqq 1における \quad f(x)=a_nx^n+a_{n-1}x^{n-1}+ \cdots +a_1x+a_0$
$\hspace{4em} の項をn乗の項から1つおきにとった \quad g(x)=a_nx^n+a_{n-2}x^{n-2}+ \cdots について$
$\hspace{6em} max|g(x)| \leqq max|f(x)|$
証明
(i)$\ n \ が偶数のとき$
$\quad g(x)=\cfrac{1}{2}(f(x)+f(-x)) だから \quad |g(x)| \leqq \cfrac{1}{2}\big(|f(x)|+|f(-x)|\big) \leqq \cfrac{1}{2}\big(max|f(x)|+max|f(-x)|\big)$
$\quad y=|f(x)| と y=|f(-x)| のグラフはy軸について対称だから \quad max|f(x)|=max|f(-x)|$
$\quad よって |g(x)| \leqq max|f(x)|$
$\hspace{5em} \therefore max|g(x)| \leqq max|f(x)|$
(ii)$\ n \ が奇数のとき$
$\quad g(x)=\cfrac{1}{2}(f(x)-f(-x)) だから$
$\quad |g(x)| \leqq \cfrac{1}{2}\big(|f(x)|+|f(-x)|\big) \leqq \cfrac{1}{2}\big(max|f(x)|+max|f(-x)|\big) = max|f(x)|$
$\quad よって max|g(x)| \leqq max|f(x)|$
(i),(ii)より $max|g(x)| \leqq max|f(x)|$
この定理を使えば、最小偏差多項式が求め易くなる。
$例1\quad 2次の最小偏差多項式$
$\hspace{2em} f(x)=ax^2+b とおける。$
$\hspace{2em} f(1)=a+b=1, \quad f(0)=b=-1 を解いて a=2$
$\hspace{2em} したがって f(x)=2x^2-1$
$例2\quad 3次の最小偏差多項式$
$\hspace{2em} f(x)=ax^3-bx$ とおける。
$\hspace{2em} f(1)=a-b=1 \hspace{20em} (1)$
$\hspace{2em} f'(x)=3ax^2-b=0 を満たす正の数を \alpha とすると$
$\hspace{2em} f'(\alpha)=0 より b=3a \alpha ^2 \hspace{16em} (2)$
$\hspace{2em} f(\alpha)=a\alpha ^3-b\alpha=-1 \hspace{18em} (3)$
(1)+(3)
$\hspace{2em} a-b+a\alpha ^3-b\alpha=0$
$\hspace{2em} (2)を代入して a \neq 0 だから 2\alpha ^3+3\alpha^2 -1=0$
$\hspace{2em} (\alpha +1)^2(2\alpha -1)=0 \quad \alpha > 0 より \alpha=\cfrac{1}{2}$
$\hspace{2em} よって a=4,\quad b=3 となり f(x)=4x^3-3x$
$例3\quad 4次の最小偏差多項式$
$\hspace{2em} f(x)=ax^4+bx^2+c$ とおける。
$\hspace{2em} f(1)=a+b+c=1 , \quad f(0)=c=1$
$\hspace{2em} \therefore b=-a$
$\hspace{2em} f'(x)=4ax^3+2bx=0 を満たす正の数を \alpha とすると$
$\hspace{2em} f'(\alpha)=0 より 2a\alpha ^2+b=0$
$\hspace{2em} \therefore 2a\alpha ^2 -a=0$
$\hspace{2em} \alpha ^2=\cfrac{1}{2} \quad \alpha > 0 より \alpha=\cfrac{1}{\sqrt{2}}$
$\hspace{2em} f(\alpha)=-1$ だから
$\hspace{2em} \cfrac{a}{4}+\cfrac{b}{2}+c=-1 \hspace{2em} \cfrac{a}{4}-\cfrac{a}{2}+1=-1$
$\hspace{2em} \therefore a=8$ よって $b=-8$
したがって $f(x)=8x^4-8x^2+1$
$以上、2次式,\ 3次式,\ 4次式の最小偏差多項式を求めたが、一般のn次式については類推のしようがない。$
$ところとが、思わぬところが関連してくるから、数学は面白い。$
メインメニュー に戻る