平方剰余
$\hspace{7em}項目6-7は別ファイルを読み込みます$
(1)$\ \ $平方剰余とは
$法3の剰余系R(3)で 1^2 \equiv 1,\ 2^2 \equiv 1 \ だから \ \ x^2 \equiv 1 \ をみたすxはx=1,\ 2 で \ x^2 \equiv 2 \ をみたすxはない。$
$そこで、1\ を\ p=3\ の平方剰余、2\ を\ p=3\ の平方非剰余といいます。$
$同様に$
$法5の剰余系R(5)で 1^2 \equiv 1,\ \ 2^2 \equiv 4,\ \ 3^2 \equiv 4,\ \ 4^2 \equiv 1 だから$
$x^2 \equiv 1をみたすxはx=1,\ 4,\ \ x^2 \equiv 4\ をみたすxは \ x=2,\ 3\ で ,\ \ x^2 \equiv 2, \ \ x^2 \equiv 3\ をみたすxはない。$
$したがって、1と4は\ p=5\ の平方剰余、2と3は \ p=5\ の平方非剰余となります。$
$一般に、次のように定義します。$
$\quad 定義 \hspace{2em}pを奇素数として 剰余系R(p)の要素aに対して$
$\hspace{5em}x^2 \equiv a \ をみたすxが存在するとき、aをpの平方剰余、存在しないとき、平方非剰余という$
$一般に、mod \ \ p \ での平方剰余は1^2,2^2,\cdots , (p-1)^2 をpで割った余りであるが、この中には同じ余りになるものもある。$
$pは奇素数だから \ \ p=2s+1 \ \ (sは整数)とおくと$
$\quad 2s+1 \equiv 0 \ \ (mod \ \ p)\ \ だから$
$\quad s+1 \equiv -s,\ \ s+2 \equiv -(s-1),\ \ \cdots , \ \ 2s \equiv -1$
$したがって平方剰余は\ \ 1^2,\ \ 2^2,\ \ \cdots ,\ \ s^2 \ \ を調べれば十分です。$
$\quad 定理1\hspace{2em}奇素数pを法とする平方剰余と平方非剰余はともに \ s \ 個ある$
$法pについて、平方剰余は \ 1^2,\ \ 2^2,\ \ \cdots ,\ \ s^2 \ \ を調べれば十分であるから、これらをpで割った余りが$
$すべて異なることを示せばよい。$
$\quad 1 \leqq a < b \leqq s \ \ である整数a,bに対して、平方剰余が等しいとすると$
$\quad b^2-a^2 \equiv 0$
$\quad (b+a)(b-a) \equiv 0$
$ところが、0 < b-a < s < p,\quad 2 < b+a < 2s < p \ \ だから \ \ b-a \ も \ b+a \ もpの倍数ではない。$
$\quad (b+a)(b-a) \not\equiv 0$
$よって、整数a,bの平方剰余は等しくないので、平方剰余はすべて異なりs個ある。$
$このことからpの平方非剰余も \ s \ 個あることがわかります。$
$例えば、p=11では平方剰余も平方非剰余もそれぞれ5個ずつあります。$
(2)$\ \ $平方剰余であるための必要十分条件(オイラーの基準)
$\quad 定理2 \hspace{2em}pを奇素数として 剰余系R(p)の要素aに対して$
$\hspace{2em}$(i)$\ \ aがpの平方剰余であるための必要十分条件は a^{\tfrac{p-1}{2}} \equiv 1$
$\hspace{2em}$(ii)$\ \ aがpの平方非剰余であるための必要十分条件は a^{\tfrac{p-1}{2}} \equiv -1$
(i)$の証明$
$必要条件$
$\quad a \equiv x^2 \ \ (mod \ \ p)\ \ ならば \quad a^{\tfrac{p-1}{2}} \equiv (x^2)^{\tfrac{p-1}{2}} \equiv x^{p-1} \equiv 1$
$なお、最後の合同ではフェルマーの定理$$(フェルマーの小定理を参照)$$が使われています。$
$十分条件$
$pの原始根$$(原始根を参照)$$の一つをhとすると、a \equiv h^r \ \ となるrが存在するから$
$\quad a^{\tfrac{p-1}{2}} \equiv (h^r)^{\tfrac{p-1}{2}} \equiv h^{\tfrac{r(p-1)}{2}}$
$左辺は1だから h^{\tfrac{r(p-1)}{2}} \equiv 1$
$hは原始根だから \cfrac{r(p-1)}{2} \ は\ p-1\ の倍数となり、\cfrac{r}{2}=l(整数)とおける。$
$よって a \equiv h^r = h^{2l}=(h^l)^2$
$h^l=x \ とおくと a \equiv x^2 となり、aはpの平方剰余である。$
(ii)$の証明$
$フェルマーの定理より a^{p-1} \equiv 1 \ \ だから$
$\quad \bigl(a^{\tfrac{p-1}{2}}-1\bigr) \bigl(a^{\tfrac{p-1}{2}}+1\bigr) \equiv 0$
$\quad a^{\tfrac{p-1}{2}} \equiv \pm 1$
$\qquad a^{\tfrac{p-1}{2}} \equiv 1 \ \ のときは aはpの平方剰余であるから、a^{\tfrac{p-1}{2}} \equiv -1 \ \ のときは aはpの平方非剰余となる。$
$例1 mod \ \ 5\ \ について \quad {\cfrac{5-1}{2}} = 2\ \ より$
$\quad 2^2 =4 \equiv -1 \ \ より\ \ 2\ \ は平方非剰余$
$\quad 3^2 =9 \equiv -1 \ \ より\ \ 3\ \ は平方非剰余$
$\quad 4^2 =16 \equiv 1 \ \ より\ \ 4\ \ は平方剰余$
$例2 mod \ \ 7\ \ について \quad {\cfrac{7-1}{2}} = 3\ \ より$
$\quad 2^3 =8 \equiv 1$
$\quad 3^3 =27 \equiv -1$
$\quad 4^3 =64 \equiv 1$
$\quad 5^3 =125 \equiv -1$
$\quad 6^3 =216 \equiv -1$
$したがって 2,\ 4\ は平方剰余、3,\ 5,\ 6\ は平方非剰余$
$ここまでは、平方剰余となるxの値を直接求めることで、aが平方剰余となるか平方非剰余となるか判別して$
$きましたが、ここからは、平方剰余となるxの値を直接求めることなく、判別する方法を考えます。$
(3)$\ \ $ルジャンドルの記号
$\quad a^{\tfrac{p-1}{2}} の値を\big(\cfrac{a}{p}\big)と表し、これをルジャンドルの記号という。$
\[
\hspace{1em}\big(\cfrac{a}{p}\big)=a^{\tfrac{p-1}{2}}=
\left\{ \begin{array}{l}
1 \hspace{4em} \cdots \quad aがpの平方剰余\\
-1 \hspace{3em} \cdots \quad aがpの平方非剰余\\
\end{array} \right.
\]
$上の例1,例2をルジャンドルの記号で表すと$
$\quad \big(\cfrac{2}{5}\big) \equiv \big(\cfrac{3}{5}\big) \equiv -1, \quad \big(\cfrac{4}{5}\big) \equiv 1$
$\quad \big(\cfrac{2}{7}\big) \equiv \big(\cfrac{4}{7}\big) \equiv 1,\quad \big(\cfrac{3}{7}\big) \equiv \big(\cfrac{5}{7}\big) \equiv \big(\cfrac{6}{7}\big) \equiv -1 $
$例 \quad \big(\cfrac{2}{11}\big) =2^{\tfrac{11-1}{2}}=2^5 =32 \equiv -1$
$\hspace{3em} \big(\cfrac{3}{11}\big) =3^{\tfrac{11-1}{2}}=3^5 =243=11 \times 22+1 \equiv 1$
(4)$\ \ $ルジャンドルの記号の性質
$ルジャンドルの記号はaがpの平方剰余かどうかを判別するのに非常に便利アイテムですので、$
$それを使いこなすためにいくつかの性質と定理を導きましょう。$
$\quad 性質1 \hspace{2em}pを奇素数として 剰余系R(p)の要素a,bに対して \ \ a \equiv b \ \ ならば \ \ \big(\cfrac{a}{p}\big) \equiv \big(\cfrac{b}{p}\big)$
$(証明)$
$a=b+kp \ \ (kは整数)とおけるから、\cfrac{p-1}{2}=s \ \ とおくと$
\begin{eqnarray*} \big(\cfrac{a}{p}\big) &=&(b+kp)^{\tfrac{p-1}{2}}\\ &=&(b+kp)^s\\ \\ &=&b^s+_sC_1b^{s-1}(kp)+_sC_2b^{s-2}(kp)^2+ \cdots + _sC_s(kp)^s\\ \\ &=&b^s+p\{ksC_1b^{s-1}+k^2p_sC_2b^{s-2}+ \cdots + k^sp^{s-1}\}\\ \\ & \equiv &b^s\\ \\ &=&b^{\tfrac{p-1}{2}}\\ \\ &=&\big(\cfrac{b}{p}\big)\\ \\ \end{eqnarray*}
$\quad 性質2 \hspace{2em}pは奇素数、abとpが互いに素ならば \ \ \big(\cfrac{ab}{p}\big) \equiv \big(\cfrac{a}{p}\big)\ \big(\cfrac{b}{p}\big)$
$(証明)$
\begin{eqnarray*} \big(\cfrac{ab}{p}\big) &\equiv & (ab)^{\tfrac{p-1}{2}}\\ &\equiv & a^{\tfrac{p-1}{2}}\ b^{\tfrac{p-1}{2}}\\ \\ &\equiv &\big(\cfrac{a}{p}\big)\big(\cfrac{b}{p}\big)\\ \end{eqnarray*}
$例\quad \big(\cfrac{6}{7}\big) =\big(\cfrac{2}{7}\big)\big(\cfrac{3}{7}\big)=1 \times (-1)=-1$
$\quad これは直接求めた値に一致しています。$
(5)$\ \ $ガウスの補助定理
$次は、一般にガウスの補助定理と言われている、平方剰余の基本的でしかも重要な定理です(おそらく)!!$
$\quad 定理3 \hspace{2em} pは奇素数とし、a\ はpの倍数でないとする。法pにおいて$
$\hspace{5em} a,\ 2a,\ \cdots ,\ \cfrac{p-1}{2}a の剰余が \ \cfrac{p}{2}\ より大きいものの個数を \ n\ とすると$
$\hspace{7em} \big(\cfrac{a}{p}\big)=(-1)^n$
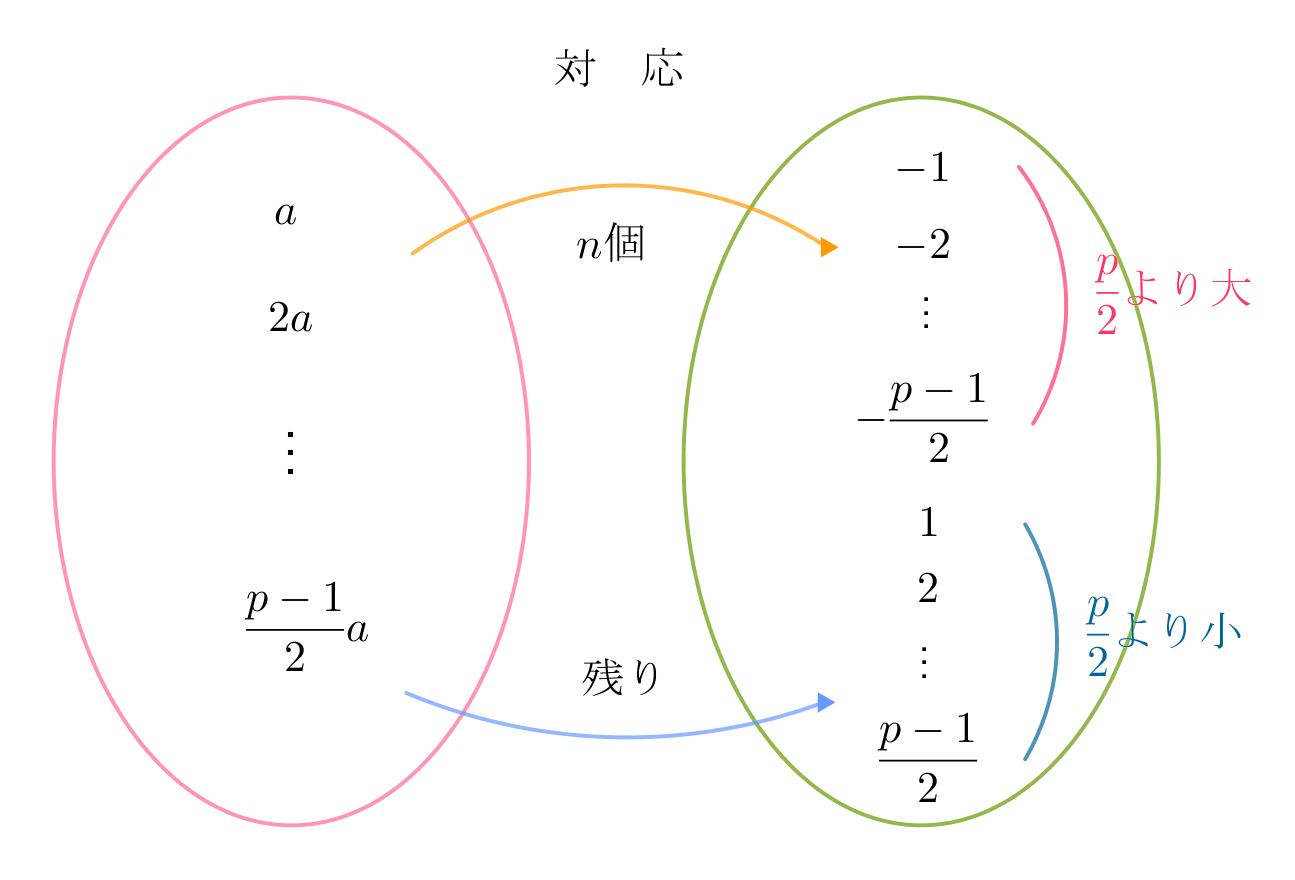
(i)$\ \ 剰余が\cfrac{p}{2}より大きいものは$
$\quad \cfrac{p+1}{2},\cfrac{p+3}{2},\cdots , p-1 \ \ があるが$
$それらは$
$\quad \cfrac{p+1}{2} \equiv \cfrac{p+1}{2}-p =-\cfrac{p-1}{2}$
$\quad \cfrac{p+3}{2} \equiv \cfrac{p+3}{2}-p =-\cfrac{p-3}{2}$
$\hspace{3em}\vdots $
$\quad p-1 \equiv -1$
$より$
$\quad -1,-2,\cdots ,-\cfrac{p-1}{2} \ \ である。$
(ii)$\ \ \{a,2a,\cdots,\cfrac{p-1}{2}a \}の法pの剰余が\cfrac{p}{2}より大きいものがn個あるから、それらは$
$\qquad \{-1,-2,\cdots ,-\cfrac{p-1}{2}\}のうちのn個であり、残りは\ \ \{1,2,\cdots ,\cfrac{p-1}{2}\}のうちのどれかである。$
$このとき、k \ne l として 例えば ka \rightarrow -2 ,\quad la \rightarrow 2 となることはない。$
$なぜならば \ \ 1 \leqq k \leqq \cfrac{p-1}{2}, \quad 1 \leqq l \leqq \cfrac{p-1}{2} \ \ として$
$ka \equiv -la \ \ とすると$
$(k+l)a \equiv 0 $
$aとpは互いに素だから \ \ k+l \equiv 0$
$ここで、2 \leqq k+l \leqq p-1 < p \ \ だから k+l \ がpの倍数になることはないので 矛盾する。よって ka \not\equiv -la$
(iii)$\ \ a,2a,\cdots,\cfrac{p-1}{2}a \ \ のうちのn個が \ \ -1,\ -2,\ \cdots ,\ -\cfrac{p-1}{2} のうちのいずれかであり、$
$\quad 残りが\ \ 1,\ 2,\ \cdots ,\ \cfrac{p-1}{2} であるから$
$\qquad a \times 2a \times \cdots \times \cfrac{p-1}{2}a \equiv (-1)^n 1 \times 2 \times \cdots \times \cfrac{p-1}{2}$
$\qquad \bigl(\cfrac{p-1}{2}\bigr)!a^{\tfrac{p-1}{2}} \equiv \bigl(\cfrac{p-1}{2}\bigr)!(-1)^n$
$\qquad \bigl(\cfrac{p-1}{2}\bigr)! \ \ と \ p\ は互いに素だから \ \ \bigl(\cfrac{p-1}{2}\bigr)! \ \ で割って$
$\qquad a^{\tfrac{p-1}{2}} \equiv (-1)^n$
$すなわち \quad \big(\cfrac{a}{p}\big) \equiv (-1)^n$
$(証明2)$
$p=2s+1 \ \ とする。$
$a,\ 2a,\ \cdots , \ sa \ \ をpで割った余りが\cfrac{p}{2}より大きいか、小さいかで分ける。$
$k_1a,\ k_2a,\ \cdots ,\ k_ma \ \ の余り \ r_1,\ r_2,\ \cdots , \ r_m \ は\cfrac{p}{2}より小さい$
$l_1a,\ l_2a,\ \cdots ,\ l_na \ \ の余り \ t_1,\ t_2,\ \cdots , \ t_n は\cfrac{p}{2}より大きいとすると$
$p-t_1,\ p-t_2,\ \cdots , \ p-t_n \ \ は\cfrac{p}{2}より小さい。$
$集合 \{r_1,\ r_2,\ \cdots , \ r_m \}と\{p-t_1,\ p-t_2,\ \cdots , \ p-t_n \}に一致する要素はない。$
$なぜならば$
$k_iaをpで割った商は\Bigl[\cfrac{k_ia}{p}\Bigr]だから \ \ k_ia=\Bigl[\cfrac{k_ia}{p}\Bigr]p+r_i \ \ とあらわされる。(除法の原理)$
$同様に、l_ja=\Bigl[\cfrac{l_ja}{p}\Bigr]p+t_j $
$r_i \equiv p-t_j \ \ とすると、法pについて$
$r_i+t_j \equiv 0$
$(k_ia-\Bigl[\cfrac{k_ia}{p}\Bigr]p)+(l_ja-\Bigl[\cfrac{l_ja}{p}\Bigr]p) \equiv 0 $
$(k_i +l_j)a \equiv 0 $
$aとpは互いに素だから \ \ k_i +l_j \equiv 0 $
$1 \leqq k_i \leqq s ,\ \ 1 \leqq l_j \leqq s \ \ より 2 \leqq k_i+l_j \leqq 2s < p$
$k_i +l_j はpの倍数でないので、k_i +l_j \equiv 0 \ \ に矛盾する。$
$よって、r_i \ne p-t_j$
$これで、r_1,\ r_2,\ \cdots ,\ r_m ,\ p-t_1,\ p-t_2,\ \cdots ,\ p-t_n \ \ は\ \ 1,\ 2,\ \cdots , \ s\ \ を並べ替えたものであることがわかりました。$
$要素のすべての積をとって$
$\hspace{3em} a\times 2a \times \cdots \times sa =s!a^s$
$一方$
$\hspace{3em} a\times 2a \times \cdots \times sa $
\begin{eqnarray*} &=&(k_1a)(k_2a)\cdots (k_ma)(l_1a)(l_2a)\cdots (l_na)\\ &=&r_1r_2\cdots r_m t_1t_2 \cdots t_n\\ &=&r_1r_2\cdots r_m (t_1-p)(t_2-p) \cdots (t_n-p)\\ &=&(-1)^nr_1r_2\cdots r_m (p-t_1)(p-t_2) \cdots (p-t_n)\\ &=&(-1)^ns!\\ \end{eqnarray*} $\qquad s!a^s=(-1)^ns!$
$\qquad \therefore a^s=(-1)^n$
$すなわち a^{\tfrac{p-1}{2}} \equiv (-1)^n$
$これをルジャンドルの記号を用いてあらわすと \qquad \big(\cfrac{a}{p}\big) \equiv (-1)^n$
メインメニュー に戻る