原始根

$フェルマーの定理$ $(フェルマーの定理を参考にしてください)$ $によれば、pが素数で、aとpが互いに素ならば$

$\hspace{5em} a^{p-1} \equiv 1 \ \ (mod \ \ p)$
$\hspace{25em}p=5 \hspace{15em}p=7$

　

$右の表は、p=5と7について、$
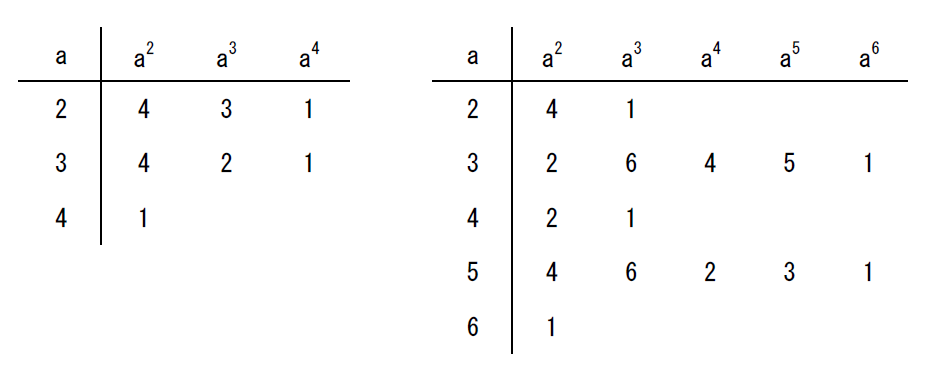
$a=2,3,\cdots , p-1 \ \ の$
$\quad a^2,a^3,\cdots , a^{p-1}$
$を計算したものです。$

$p=5 では、a=2と3は4乗して$
$はじめて1になり、$
$p=7 では、a=3と5は6乗して$
$はじめて1になることがわかります。$

$そこで次のように、定義します。$

$\hspace{2em}定義 \quad pが素数で、aとpは互いに素とする。$
$\hspace{5em}aをp-1乗してはじめて1と合同になるとき、aをpの原始根という$

　

$連立合同式$$(連立合同式を参照)$$でも触れましたが、$
$pが素数ならば、剰余系R(p)=Z/pZ=\{0,1,2,\cdots ,p-1\} はpを法として$
$体となりました。$

$例えば、R(5)の積の演算表は右表のとおりで、巡回群になります。$

$\quad 2^1=2,\ \ 2^2=4,\ \ 2^3=3,\ \ 2^4=1 \ \ ですから2は生成元です。$

$\quad 3^1=3,\ \ 3^2=4,\ \ 3^3=2,\ \ 3^4=1 \ \ ですから3も生成元です。$

$すなわち、生成元は原始根です。$

　

$R(7)の積の演算表は右表のとおりで、やはり巡回群です。$

$\quad 3^1=3,\ \ 3^2=2,\ \ 3^3=6,\ \ 3^4=4,\ \ 3^5=5,\ \ 3^6=1$

$ですから3は生成元です。$

$\quad 5^1=5,\ \ 5^2=4,\ \ 5^3=6,\ \ 5^4=2,\ \ 5^5=3,\ \ 5^6=1$

$ですから5も生成元です。$

$やはり、生成元は原始根です。$


$定理1$
$\hspace{2em}素数pの法の原始根aに対して、G=\{a,a^2,\cdots,a^{p-1}\}\ \ で \ \ 1 \leqq i \leqq p-1,\ \ 1 \leqq j \leqq p-1 \ \ のとき$
$\hspace{6em}i \ne j \ \ \rightarrow \ \ a^i \ne a^j$

$証明$

$対偶を示します$
$法pについて　a^i \equiv a^j \ \ ならば \ \ a^{i-j} \equiv 1$
$一般に、フェルマーの定理から \ \ aとpが互いに素ならば　a^{p-1} \equiv 1　だから \ \ i-j \ \ は \ \ p-1 \ \ の倍数である。$
$ところが、-p+2 \leqq i-j \leqq p-2 \ \ だから \ \ 　-(p-1) < i-j < p-1$
$これを満たすのは　i-j=0 \ \ のときだけだから　i=j$

$\hspace{3em}aが素数pの原始根ならば　G=\{a,a^2,\cdots , a^{p-1}\}の要素はすべて異なり、$
$\hspace{3em}Gは \ R(p)=\{1,2,\cdots , p-1\} \ \ に一致する。$


$これで、R(p)は原始根を生成元とする巡回群になることがわかりました。$


$定理2$
$\hspace{1em} 巡回群R(p)の生成元の一つをaとし、p-1と互いに素な正の整数をmとすると、a^m \ はまた生成元となる。$

$(証明)$

$R(p)の位数 \ p-1\ をsとする。$
$a^mのs個の累乗 \ a^m,\ \ a^{2m},\cdots , a^{sm} \ \ が異なっていればよい。$

$対偶を示します$
$法pについて　a^{im} \equiv a^{jm} \ \ ならば　a^{(i-j)m} \equiv 1$
$したがって、(i-j)m \ \ はR(p)の位数 \ s=p-1\ の倍数である。$
$mとsは互いに素だから、(i-j)がsの倍数である。$
$ところが、1 \leqq i \leqq s,\ \ 1 \leqq j \leqq s \ \ だから -(s-1) \leqq i-j \leqq s-1 \ \ より　-s < i-j < s$
$これを満たすのは　i-j=0 \ \ のときだけだから　i=j$


$定理3 \qquad 素数pの原始根は \ \varphi(p-1) \ 個ある。$

$(証明)$

$定理2より巡回群R(p)の生成元の一つをaとし、s=p-1と互いに素な正の整数をmとすると、$
$a^mはまた生成元となるから、原始根の個数はsと互いに素な正の整数の個数、すなわち\varphi(p-1)個ある。$


$具体例で考えましょう。$

$例1$
$R(5)=\{1,2,3,4\}の生成元の一つは2であった。$
$位数は \ s=4 \ だから、\varphi(4)=2 \ で生成元はもう一つある。$
$sと互いに素な数は3だから \ \ 2^3 \equiv 3 \ \ (mod \ \ 5)\ \ が生成元である。$
$3^1=3,\ \ 3^2=4,\ \ 3^3=2,\ \ 3^4=1\ \ ですから確かに3も生成元であることは前にも示しました。$


$例2$
$R(7)=\{1,2,3,4,5,6 \}の生成元の一つは3であった。$
$位数は \ s=6 \ だから、\varphi(6)=2 \ で生成元はもう一つある。$
$sと互いに素な数は5だから \ \ 3^5 \equiv 5 \ \ (mod \ \ 7)\ \ が生成元である。$
$5^1=5,\ \ 5^2=4,\ \ 5^3=6,\ \ 5^4=2,\ \ 5^5=3,\ \ 5^6=1\ \ ですから確かに5も生成元であることは前にも示しました。$

$以上のことから、素数pに対し、R(p)の原始根は\varphi(p-1)個あるが、$
$それらの最小の原始根が求まればよいことがわかりました。$


$例3$
$次表はR(11)の原始根2の積の演算表です。$

　

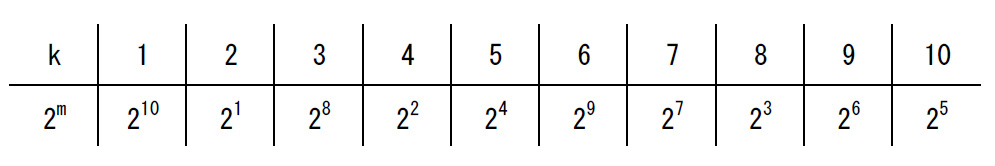
$s=10ですから　\varphi(10)=4 より原始根は他に3つあります。$
$sと互いに素な数は \ \ 3,\ \ 7,\ \ 9\ \ があります。$
$mod \ \ 11 で　2^3 \equiv 8,\ \ 2^7 \equiv 7,\ \ 2^9 \equiv 6 \ \ だからそれらをを生成元とすると、次表が演算表です。$

　
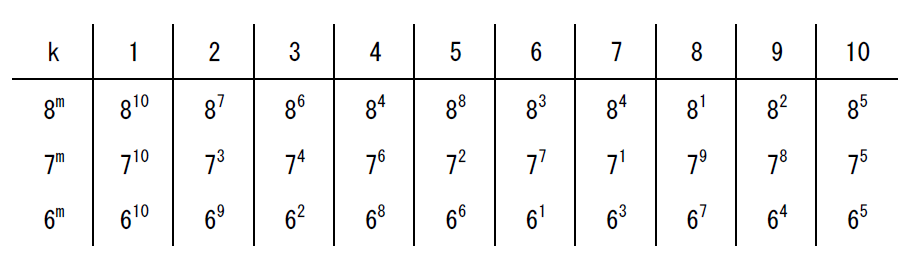
$例4$
$R(13)の最小の原始根は2です。$
$s=12ですから　\varphi(12)=4 で、sと互いに素な数は、\{1,5,7,11 \}です。$
$したがって、原始根は他に3つあります。$
$mod \ \ 13 \ で　2^5 \equiv 6,\ \ 2^7 \equiv 11,\ \ 2^{11} \equiv 7 \ \ だから、原始根は6,\ \ 11,\ \ 7\ \ です。$


$原始根を求めることはこのくらいにして、原始根を使った定理の証明を考えましょう。$

$定理3 \hspace{2em}pは素数で、kがp-1で割り切れないならば \quad 1^k+2^k+\cdots +(p-1)^k \equiv 0 \quad (mod \ \ p)$

$(証明)$

$pの原始根の一つをaとすると、pを法として$
$集合 A=\{1,2,\cdots ,p-1\}と集合 B=\{a,a^2,\cdots,a^{p-1}\}は一致する。$
$したがって \ \ t \in A \ \ に対して　s \in A \ \ があって　t=a^s$
$\quad t^k=(a^s)^k=a^{sk}$
$ここで、k=(p-1)q \quad (qは整数)\ \ ならば$
$\quad t^k =t^{(p-1)q}=(t^{p-1})^q \equiv 1 $
$となるので、kはp-1で割り切れないという条件をつけましょう。$

$すると、\{1^k,2^k,\cdots ,(p-1)^k\}=\{a^k,a^{2k},\cdots ,a^{(p-1)k}\} \ \ だから$

$\hspace{4em}1^k+2^k+\cdots +(p-1)^k $
\begin{eqnarray*} &=&a^k+a^{2k}+\cdots +a^{(p-1)k} \hspace{5em}\\ \\ &=&\cfrac{a^k \{(a^k)^{p-1}-1 \}}{a^k-1}\\ \\ &=&\cfrac{a^k \{a^{p-1})^k-1 \}}{a^k-1}\\ \\ &=&\cfrac{a^k(1^k-1)}{a^k-1}\\ \\ &\equiv &0\\ \end{eqnarray*}

$\qquad 定理4 \quad (ウィルソンの定理) \qquad p が素数ならば　(p-1)! \ \equiv \ -1 \ \ (mod \ \ p)$　


$(証明)$

(i)$\ \ p=2のとき$

$\quad mod \ \ 2\ \ で　\quad (2-1)!=1 \equiv -1 \quad (mod \ \ 2)$

(ii)$\ \ pが奇素数のとき$

$\quad 素数pの原始根の一つをaとする。$
\begin{eqnarray*} \quad (p-1)! &=&1 \times 2 \times \cdots \times (p-1)\\ \\ &=&a \times a^2 \times \cdots \times a^{p-1}\\ \\ &=&a^{1+2+\cdots + (p-1)}\\ \\ &=& a^{\tfrac{(p-1)p}{2}}\\ \\ &=&\Bigl(a^{\tfrac{p-1}{2}}\Bigr)^p\\ \end{eqnarray*} $\quad ここで、\Bigl(a^{\tfrac{p-1}{2}}\Bigr)^2=a^{p-1} \equiv 1 \quad だから \quad a^{\tfrac{p-1}{2}}　\equiv \pm 1$

$\quad aは原始根だから(p-1)乗ではじめて1になるので、a^{\tfrac{p-1}{2}} \equiv 1 \ \ は不適$

$\quad よって　a^{\tfrac{p-1}{2}} \equiv -1$

$\quad pは奇素数だから \quad (p-1)! \equiv (-1)^p =-1$



　

ページの先頭へ↑




メインメニュー　に戻る