1 ビュフォンの針の問題とは
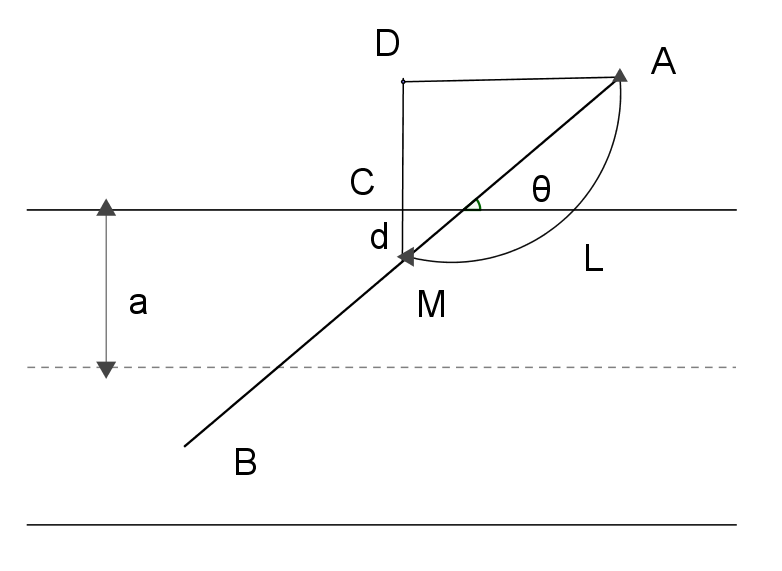
$上から長さ2L(L\leqq \ a)の針をランダムに落とす$
$とき、この針が平行線と交わる確率を求める問題が$
$「ビュフォンの針の問題」である。$
$平行線はたくさんあるから、落ちた針の中点Mを$
$挟む2つの平行線を考え、対称性から点Mが、この$
$2本の平行線の中間の直線の上側にある場合(下側$
$でも同じということ)を考えれば十分である。$
$落とされた針の位置は、針と平行線のなす角\theta、および点Mと平行線との距離dで確定する。$
$(Mの平行線方向の成分は関係しない。)$
$針はランダムに落とされるから、\theta は [ 0, \pi] , d は [ 0, a ] で一様な値をとる連続型の確率変数で、$
$全事象は$
$\hspace{3em} \Omega = {( \theta , d ) \mid 0 \leqq \theta \leqq \pi , 0 \leqq d \leqq a}$
$\hspace{2em} MC\ \leqq MD だから$
$\hspace{2em} d\ \leqq L\sin \theta$
$したがって、交わる事象A は$
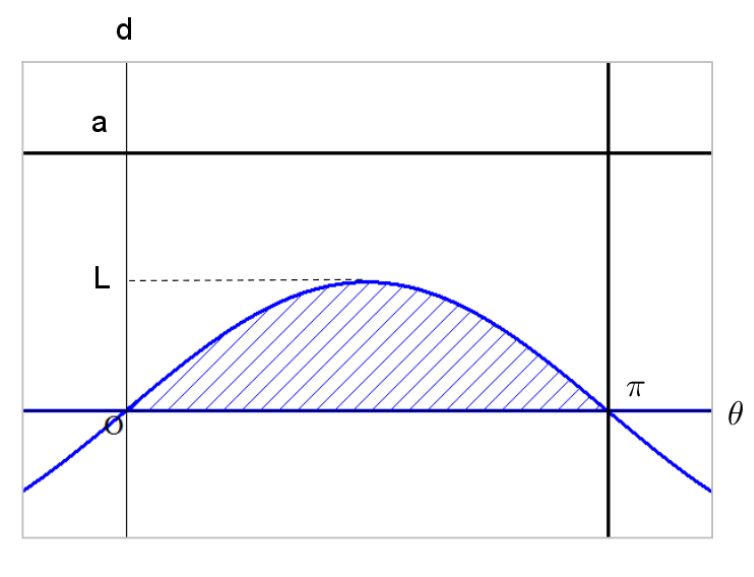
$\hspace{2em} A =\{(\theta , d ) \mid d \leqq L\sin \theta \}$
$となる。$
$この問題の測度mは面積と考えると、$
$\hspace{3em} m(\Omega)=\pi a$ \[m(A) = \int_{0}^{\pi} L \sin \theta d\theta = -L\left[\ \cos \theta \ \right ]_0^\pi=2L \hspace{32em}\] \[\therefore \ P(A) = \cfrac{m(A)}{m(\Omega)} = \cfrac{2L}{\pi a} \hspace{41em}\]
$これがこの問題の答えである。$
$針を落とす回数をN、そのうち平行線と交わった回数をkとする。$
$Nを十分大きく取れば、相対度数 \cfrac{k}{N} は大数の法則により、確率P(A) と見なせるから$
$\hspace{3em} \cfrac{2L}{\pi a}=\cfrac{k}{N} \ より \pi=\cfrac{2L}{a} \times \cfrac{N}{k} $
$となって、ビュッフォンの針の問題は、問題としての面白さに加えて、実験的に\pi の値を$
$求めることができることにある。(と勝手に思っている)$
2 モンテカルロ法による実験
$実際に針をランダムに何回も落とすという試行は、乱数を用いたモンテカルロ法で代行する。$
$落ちた針の状況は、平行線となす角 \theta 、針の中点の座標のうち、垂直成分yで決定されるから、$
$その2つの変数を乱数で与えればよい。$
$ただし、一般にコンピュータで発生させる乱数は0から1の一様乱数であるから、これをうまく変換して使う。$
$Excel VBAを用いて、a=2, \ L=2 とし、N=2000 を1セットとして10セット繰り返した結果が下表です。$
$kは累積度数です。$
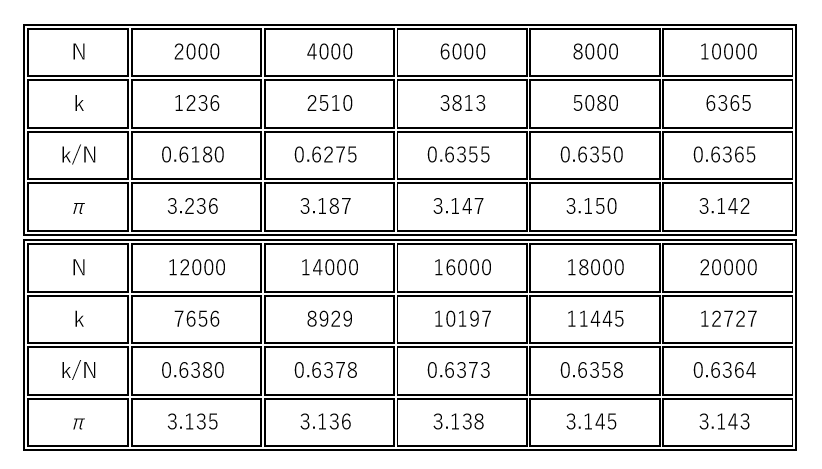
$\pi の値が3.14まで出ました。おそらくこれ以上の精度はモンテカルロ法の限界で、$
$丸め誤差や一様乱数の発生状況などから期待できないと思われます。$
$模造紙に平行線を引いて、縫い針を何本も投げる実験を行えばきっともっといい値が$
$得られるかもしれません。$
円周率 $π$ の話 に戻る
メインメニュー に戻る