球面における正弦定理
$※\ \ 球面三角形についての予備知識は($地球上の2地点間の距離$)を参照してください$
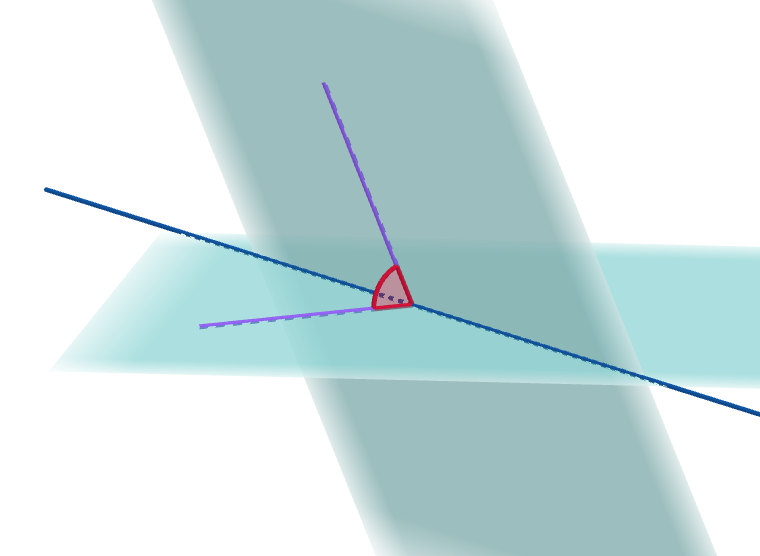
定義 2平面のなす角
$交わる2平面の交線上の点から、2つの平面上に交線に垂直に引いた$
$2直線のなす角を2平面のなす角といいます。$
定理1
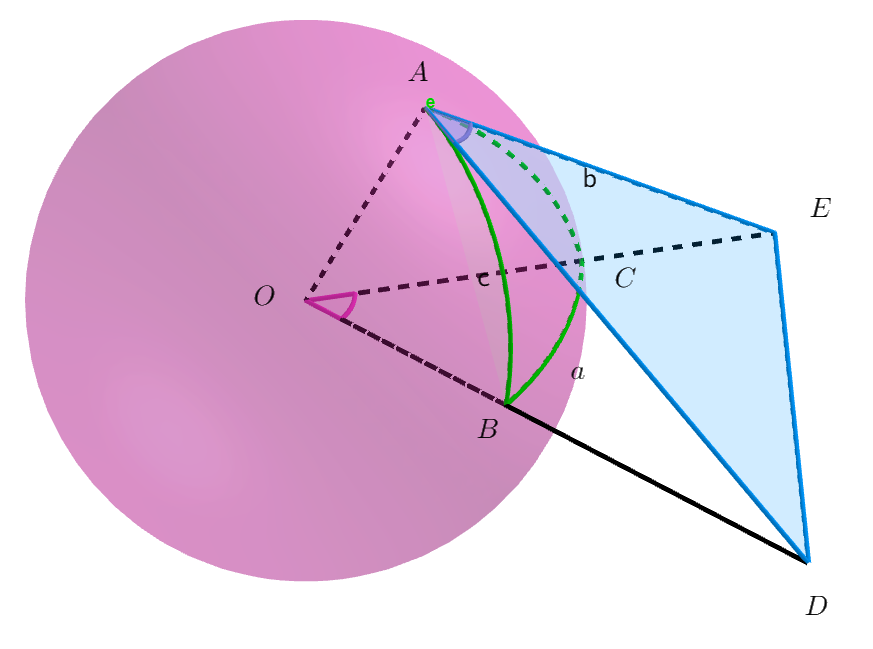
$右図ように、中心Oの球面三角形ABCの頂点Aにおいて、$
$弧ABの接線と直線OBの交点をD、弧ACの接線と直線OCの$
$交点をEとする。$
$\triangle{OAD}と\triangle{OAE}がつくる平面をそれぞれ\alpha ,\betaとすると$
$弧ABと弧ACのなす角は、2平面 \alpha と\betaがなす角に等しい。$
$(証明)$
$弧ABの点Aにおける接線は平面\alpha 上にあり、$
$弧ACの点Aにおける接線は平面\beta 上にある。$
$また、点Aは球面上の点だからOAと接平面は垂直である。$
$線分ADとAEは接平面上にあるから、$
$\quad OA \perp AD,\quad OA \perp AE$
$ここで、OA は2平面\alpha,\beta の交線だから、2平面のなす角の定義から$
$平面\alpha 上の線分ADと平面\beta 上の線分AEのなす角が2平面\alpha,\beta のなす角になる。$
$したがって、弧ABと弧ACのなす角は、2平面 \alpha と\betaがなす角に等しい。$
定理2
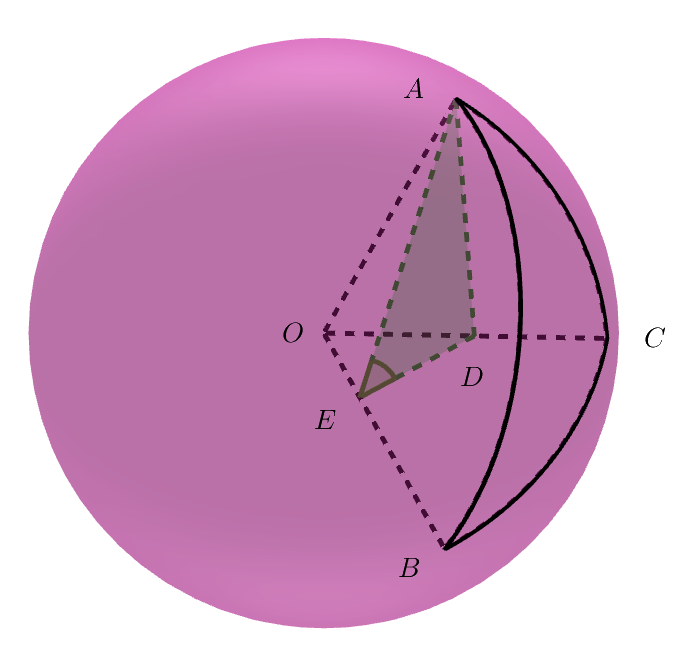
$右図ように、\angle C=90°の球面三角形ABCにおいて、$
$頂点AからOCに垂線ADを引き、点DからOBに垂線DEを引く。$
$このとき、\angle AED は平面OABと平面OACのなす角に等しい。$
$(証明)$
$\angle C=90°だから、定理1より平面OACと平面OBCは直交する。$
$したがって、AD \perp 平面OBC より AD \perp OB$
$仮定から DE \perp OB $
$したがって、三垂線の定理により、AE \perp OB$
$\hspace{3em}(三垂線の定理は$三垂線の定理$を参照してください)$
$よって、定義から\angle AED は2つの平面OBAと平面OBCのなす角である。$
$またこれは定理1より、\angle Bに等しくなる。$
$このことから、次の正弦定理を導くことができる。$
正弦定理
$(1)\ \ \angle C=90°のとき$
$半径1の球面で考えると \ \ OA=OB=OC=1$
$\quad AD=OA\sin \angle AOD =\sin \angle AOC =\sin b$
$\quad AE=OA\sin \angle AOE =\sin \angle AOB =\sin c$
$直角三角形ADEにおいて、定理2より \angle AED=\angle B \ \ だから$
$\quad \sin B=\sin \angle AED =\cfrac{AD}{AE}=\cfrac{\sin b}{\sin c} \quad \therefore \sin c=\cfrac{\sin b}{\sin B}$
$全く同じことを頂点Aでおこなうと$
$\quad \sin A=\cfrac{\sin a}{\sin c} \ \ が得られるから \ \ \sin c=\cfrac{\sin a}{\sin A}$
$したがって \quad \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B} $
$(2)\ \ \angle C \ne 90°のとき$
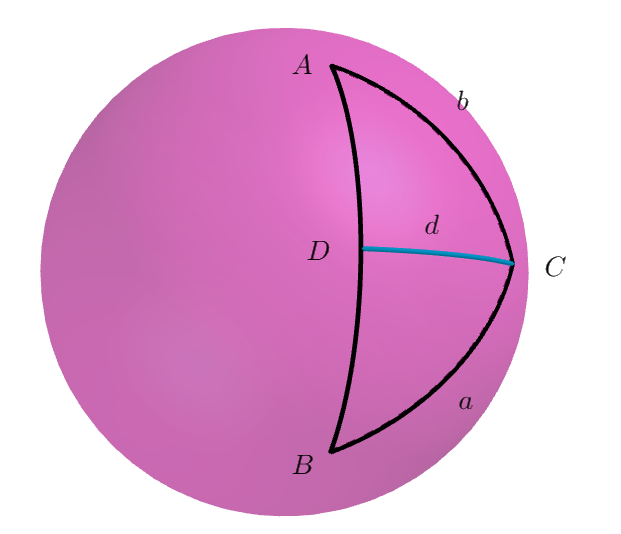
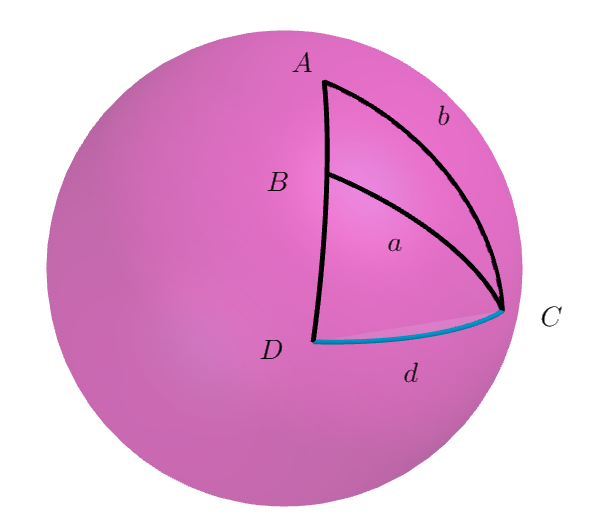
(i)$点Cから弧AB上に直交する弧CDが引ける場合$
$弧CD=d \ とする$
$球面三角形ACD において \sin b=\cfrac{\sin d}{\sin A} \quad \therefore \sin d=\sin A \cdot \sin b$
$球面三角形BCD において \sin a=\cfrac{\sin d}{\sin B} \quad \therefore \sin d=\sin B \cdot \sin a$
$したがって \quad \sin A \cdot \sin b=\sin B \cdot \sin a \ \ より \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B} $
(ii)$点Cから弧ABの延長上に直交する弧CDが引ける場合$
$球面三角形 ACD で \sin b=\cfrac{\sin d}{\sin A} \therefore \sin d=\sin A \cdot \sin b$
$\angle CBD \ は\angle ABC \ の隣角だから \ \ \angle CBD =180°-\angle ABC=180°-B$
$球面三角形 BCD で \sin a=\cfrac{\sin d}{\sin (180°-B)}=\cfrac{\sin d}{\sin B} \quad \therefore \sin d=\sin B \cdot \sin a$
$したがって \quad \sin A \cdot \sin b=\sin B \cdot \sin a \ \ より \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B} $
(i)(ii)$より \angle C \ne 90°のときも\ \ \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B} \ \ が成りたつ。$
$(1)(2)より、任意の球面三角形で \quad \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B} \ \ が成りたつ。$
$この関係は\sin C \ と \ \sin c \ \ についても同様にいえるから$
$\qquad \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B}=\cfrac{\sin c}{\sin C}$
$これを球面三角形の正弦定理といいます。$
$\quad 球面三角形の正弦定理$
$\qquad \cfrac{\sin a}{\sin A}=\cfrac{\sin b}{\sin B}=\cfrac{\sin c}{\sin C}$
$※\ \ 球面三角形の余弦定理は($地球上の2地点間の距離$)を参照してください$
メインメニュー に戻る