地球上の2地点間の距離
$地球は球体ですから、遠く離れた2地点の距離は、平面上の直線距離で求めることはできません。$
$平面上では、三角形の余弦定理を用いて2点間の距離が求められますので、球面上でも同じような$
$ことが考えられるのではないでしょうか。$
$そこで、まず球面上の三角形から考えてみましょう。$
1 球面三角形
$(1)\ \ 球面三角形とは$

$球面三角形とは右図のように、球面上の3点(頂点といいます)のうち、2点を通る$
$3つの大円(中心が球の中心に一致する円)で囲まれた図形です。$
$ですから$
$辺は大円の円弧で、角は円弧と円弧のなす角になりますので、平面上の三角形の$
$内容とは大きく異なります。$
$(2)\ \ 球面三角形ABCの要素$

(i)$辺$
$弧BCを辺aとかき、その長さもaであらわす。$
$同様に弧CA,ABをそれぞれb,cであらわす。$
$球面の半径を1とすると、扇形OBCについて、弧BC=1 \times \angle BOC だから$
$\qquad \angle BOC=a$
$同様にして、\angle COA=b,\quad \angle AOB =c$
(ii)$角$
$弧ABと弧ACのなす角をやはりAとかく。角B,Cについても同様である。$

$なお、一般に2曲線のなす角とは$
$交わる2曲線の交点をPとし、点Pにおける2曲線の接線がつくる$
$平面(接平面という)上で、2つの接線のなす角のことである。$
$球面三角形についても、角頂点における2つの弧の接線の$
$なす角のことである。$
2 余弦定理

$右図のような半径1の球面で、球面三角形ABCの辺a,b,c と角Aとの間に$
$成りたつ関係を調べましょう。$
$平面ADEは、点Aにおける球Oの接平面です。$
$よって、OA \perp 平面ADE \ \ より OA \perp AD,\quad OA \perp AE$
$したがって \quad \triangle ODA と\triangle OEA は直角三角形となる。$
$また、\quad \angle DOE=\angle BOC=a,\quad \angle DOA=\angle BOA=c $
$\triangle{ODE} \ と \ \triangle{ADE} \ に平面三角形の余弦定理を用いて$
$\quad DE^2=OD^2+OE^2-2OD\cdot OE\cos a$
$\quad DE^2=AD^2+AE^2-2AD\cdot AE\cos A$
$辺々引いて$
$(OD^2-AD^2)+(OE^2-AE^2)-2OD\cdot OE\cos a+2AD\cdot AE\cos A=0$
\begin{eqnarray*}
2OD\cdot OE\cos a
&=&(OD^2-AD^2)+(OE^2-AE^2)+2AD\cdot AE\cos A\\
&=&OA^2+OA^2+2AD\cdot AE\cos A\\
&=&2OA^2+2AD\cdot AE\cos A\\
\end{eqnarray*}
$\therefore OD\cdot OE\cos a=OA^2+AD\cdot AE\cos A$
\begin{eqnarray*}
\cos a
&=&\cfrac{OA^2}{OD\cdot OE}+\cfrac{AD\cdot AE}{OD\cdot OE}\cos A\\
\\
&=&\cfrac{OA}{OE}\cdot \cfrac{OA}{OD}+\cfrac{AE}{OE}\cdot \cfrac{AD}{OD}\cos A\\
\\
&=&\cos b \cdot \cos c +\sin b \cdot \sin c \cdot \cos A\\
\end{eqnarray*}
$これを、球面三角形の余弦定理といいますが、平面三角形の余弦定理とは似ても似つかない形をしています。$
$球面三角形の余弦定理$
$\qquad \cos a=\cos b \cdot \cos c +\sin b \cdot \sin c \cdot \cos A$
3 地球上の2地点間の距離
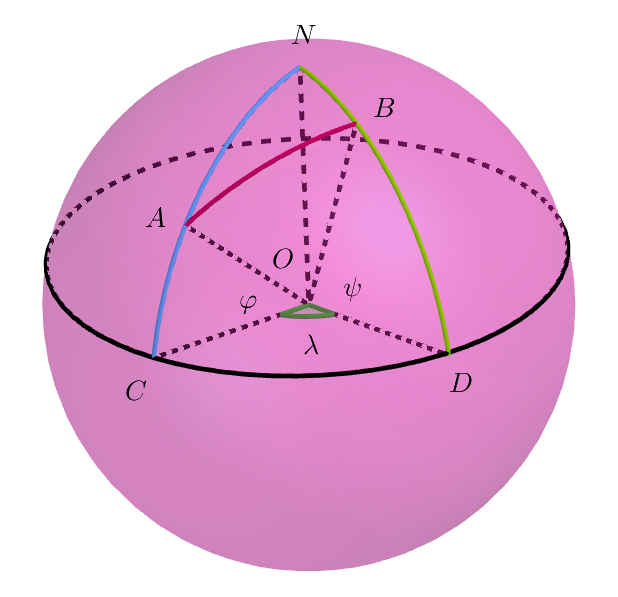
$地点A,Bの緯度を\varphi,\psi とし、経度の差を\lambda とする。$
$右図で、Nは北極点です。$
$球面三角形NABに余弦定理を用いて、AB間の距離を求めましょう。$
$\quad \angle NOA = 90^{\circ}- \varphi ,\quad \angle NOB = 90 ^{\circ}- \psi $
$\quad \angle AOB = \theta \ \ とおくと$
\begin{eqnarray*} \cos \theta &=&\cos (90 ^{\circ}-\varphi)\cos (90^{\circ}-\psi)+\sin (90^{\circ}-\varphi)\sin (90^{\circ}-\varphi)\cos \lambda\\ \\ &=&\sin \varphi \sin \psi +\cos \varphi \cos \varphi \cos \lambda\\ \end{eqnarray*} $これより \theta を求めると、$
$L=弧AB=R\theta \ \ (ただし Rは地球の半径) より2地点間の距離が求まります。$
$地球上の2地点間の距離$
$\qquad L=R\cos ^{-1}(\sin \varphi \sin \psi +\cos \varphi \cos \varphi \cos \lambda)$
$下表は、Excel \ を用いて、東京スカイツリーとエジプトの3大ピラッミドのあるギザ間の距離を求めたもので、$
$a \ は第1項、b \ は第2項、c \ はそれらの和、すなわち\cos \theta \ の値です。$
$\theta を表ではxと置き換えてあります。$

$※\ \ 球面三角形の正弦定理は($球面三角形の正弦定理$)を参照してください$
メインメニュー に戻る