MY MATH NOTE

三垂線の定理

1 直線と平面の直交(1)

　
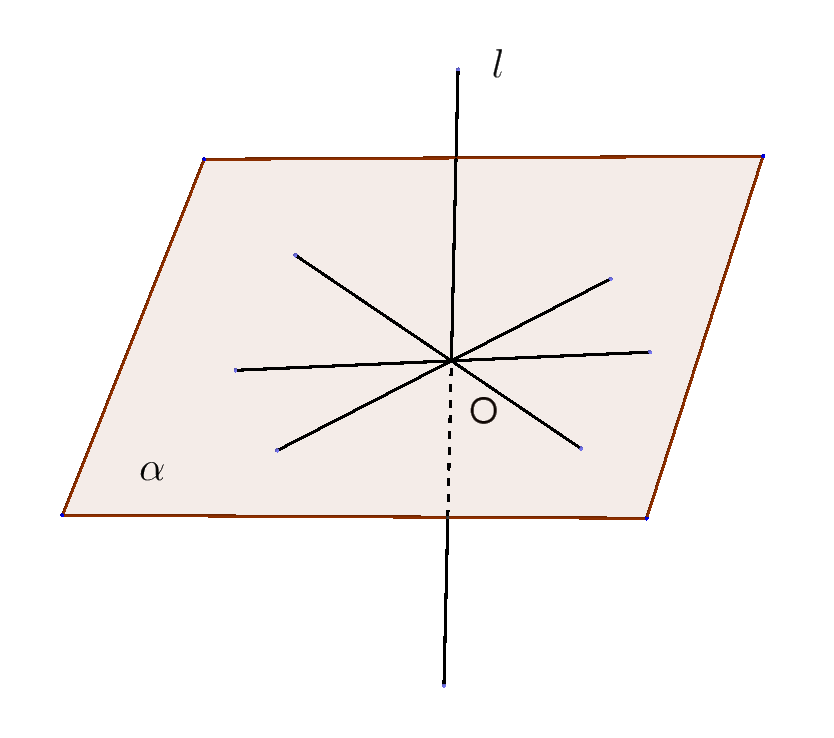
$\quad 定義$
$空間において、直線 \ lと平面\alpha が交わるとき、その交点Oを$
$通る \alpha 上のすべての直線が \ l \ と垂直のとき、l \ は\alpha に垂直で$
$あるといい、l \perp \alpha \ と書く。$

$\quad 定理1$
$空間において、直線 \ l \ と平面 \alpha が点Oで交わるとき、Oを$
$通る\alpha 上の2直線が、l \ と垂直ならば、l \ は\alpha に垂直である。$

これは、高校の教科書にも載っている（いた？）定義と定理であるが、釈然としないものがある。
$それは、定義に「\alpha 上のすべての直線」を持ち出している点である。$

$それが定理1で「\alpha 上の2直線」でよいと証明されるが、ならば、なぜ定理1と定義を$
入れ換えないのかと疑問が湧くのである。

そこで

$\quad 新定義$
$空間において、直線 \ l \ と平面\alpha が点Oで交わるとき、その交点Oを通る\alpha 上の2直線が \ l \ と$
$垂直のとき、l \ は\alpha に垂直であるといい、l \perp \alpha \ \ と書く。$

　
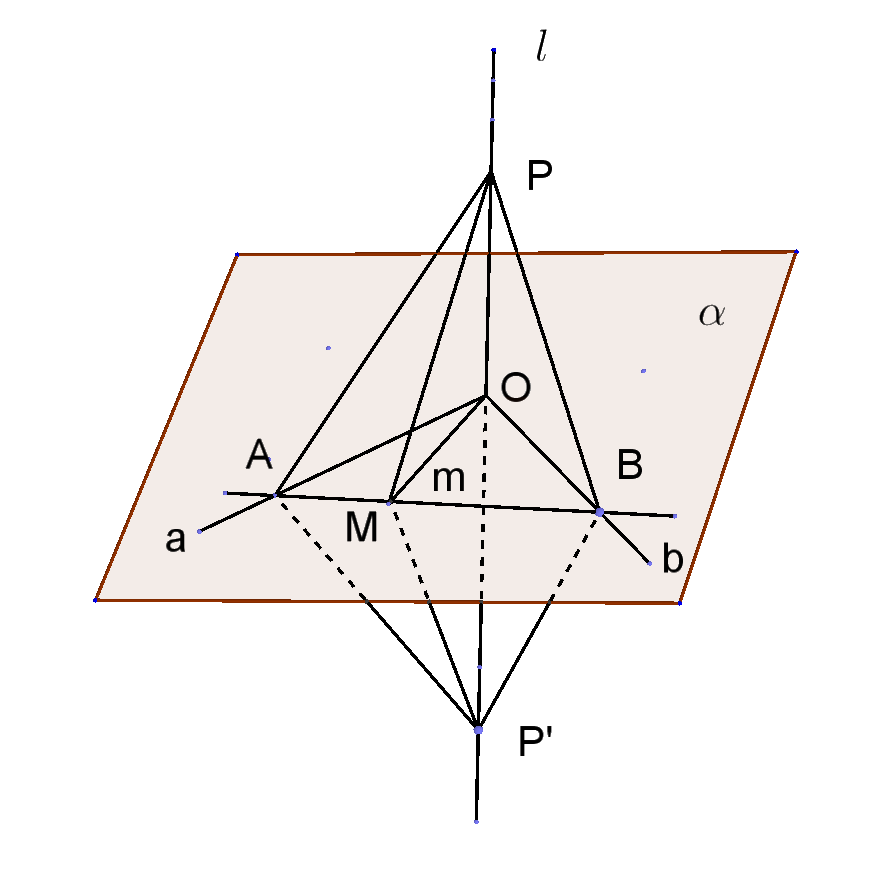
$\quad 新定理1$
$空間において、直線 \ l \ と平面\alpha が垂直ならば、その交点Oを通る、$
$\alpha 上のすべての直線は\alpha に垂直である。$

$(証明)$
$直線 \ l \ 上で、点Oを挟んだ両側に2点P,P'$
$をとって \ OP=OP' \ とする。$
$直線 \ l \ と平面\alpha が垂直だから、新定義よりOを$
$通る\alpha 上の２直線 a、b は \ l \ と垂直である。$

$a,b上にOと異なる点をとり、それぞれA，Bとする。$
$Oを通る\alpha 上の任意の直線を m とし、直線ABとの交点をMとする。$
$(任意の直線m でいえれば、すべての直線で成りたつことになる。）$

(i)$\ △OAPと△OAP'において$
$\qquad ∠AOP=∠AOP'=90°, \ OP=OP' , \ OAは共通$
$\qquad よって、２辺とその間の角が等しいから　△OAP \equiv △OAP'$
$\qquad したがって　AP=AP'$

(ii)$\ △OBPと△OBP'において$
$\qquad $ (i)と同様にして　$△OBP \equiv △OBP' より、BP=BP' $

(iii)$\ △ABPと△ABP'において$
$\qquad $(i),(ii)より$AP=AP' , BP=BP', ABは共通$
$\qquad よって　3辺が等しいから　△ABP \equiv △ABP'$

(iv)$\ △AMPと△AMP'において$
$\qquad $(i)より　$AP=AP'$
$\qquad $(iii)より $∠MAP=∠MAP'$
$\qquad AMは共通$
$\qquad よって、2辺とその間の角が等しいから、△AMP \equiv △AMP'$

(v)$\ △OMPと△OMP'において$
$\qquad 仮定より　OP=OP'$
$\qquad $(iv)より　$MP=MP'$
$\qquad OMは共通$
$\qquad よって、3辺が等しいから　△OMP \equiv △OMP'$

$したがって　∠POM=∠P'OM　となり　∠POM=90°$
$すなわち　l \perp m$


このように、定義と定理1を入れ換えた新定義と新定理1でも同じであるのだが、なぜ昔の偉い
先生は、このような方法をとったのであろうか。
定義はなるべく幅広く取った方がその後の展開に都合がいいからか。浅学の私にはわからない。


もう少し続けます。ここからは、よくある内容です。！！

2 平面上の交わる2直線と垂直な直線

　
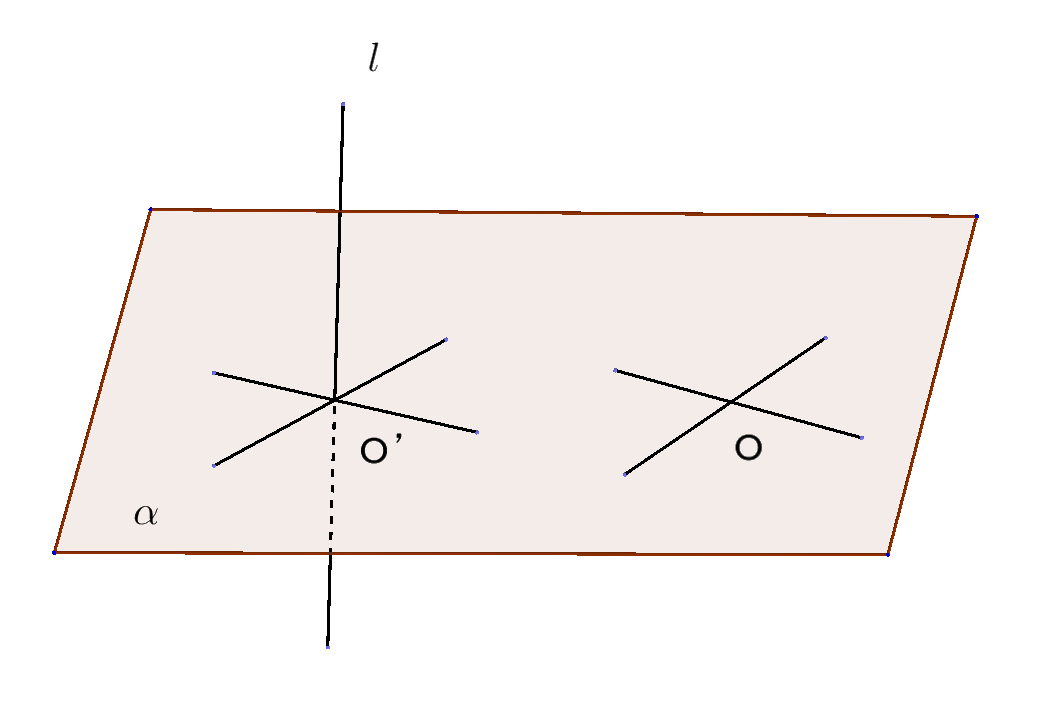
$\quad 定理2$
$直線 \ l \ が、平面\alpha と点O'で交わっている。l \ が、\alpha 上の$
$点Oで交わる２直線 a、bに垂直ならば、l \ は\alpha に垂直である。$
これを式で表すと
$\hspace{3em} l \perp a、l \perp b \rightarrow 　l \perp \alpha $

$(証明)$
$平面\alpha 上で、点O'を通り、a、bに平行な直線をそれぞれ a',b'とする。$
$l \ とaのなす角は、l \ とa'のなす角に等しいので、$
$\qquad l \perp a　より　 l \perp a'$

$同様にして　l \perp b　より　 l \perp b'$

$よって、　l \ は点O'で交わる\alpha 上の2直線に垂直だから定理1より　l \perp \alpha $

3 直線と平面の直交(2)

　
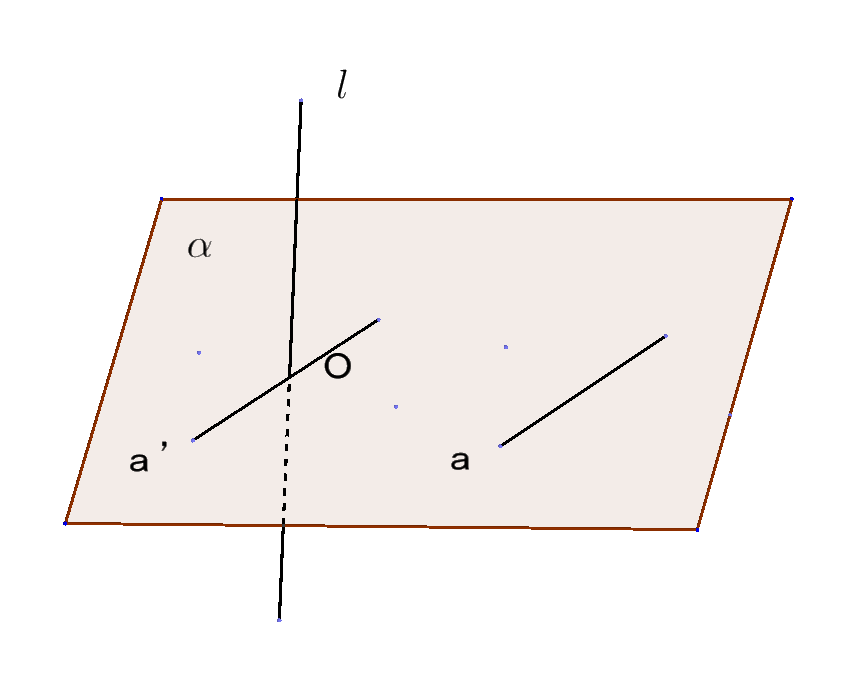
$\quad 定理3$
$直線 l と平面\alpha が垂直ならば、l \ は\alpha 上のすべての（任意の）$
直線に垂直である。

$(証明)$
$l \ と\alpha の交点をOとし、\alpha 上の任意の直線を a とする。$
$a に平行でOを通る直線を a' とすると$
$\qquad l \perp \alpha 　より　l \perp a'$

$よって \ l \ は a に垂直となる。$

4 三垂線の定理

　
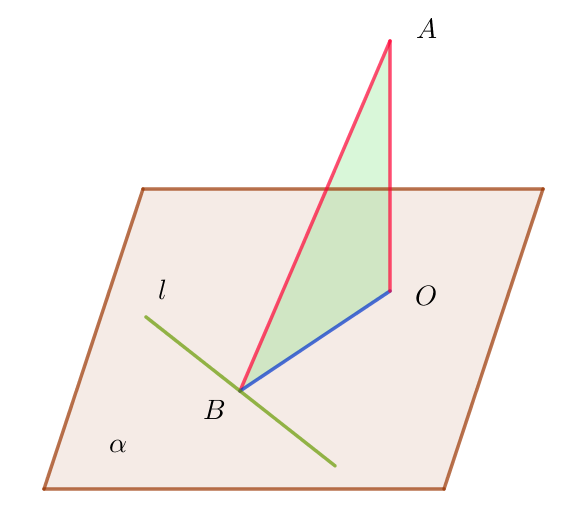
$(1型)$
$平面\alpha 外の点Aより\alpha に下ろした垂線の足をO、Aより$
$平面\alpha 上の直線 \ l \ に下ろした垂線の足をBとすれば、$
$OBと \ l \ は直交する。すなわち$

$\qquad AO \perp \alpha 、AB \perp l \ \ \rightarrow \ \ OB \perp l$

$(証明)$
$AO⊥\alpha で、l \ は平面\alpha 上の直線だから、定理3より　AO \perp l$
$仮定より　AB \perp l　だから、 l \ は点Aで交わる2直線AO,ABに垂直となり$
$定理2より　 l \perp (平面ABO)$
$よって、OBは平面ABO上の直線だから　OB \perp l $

　
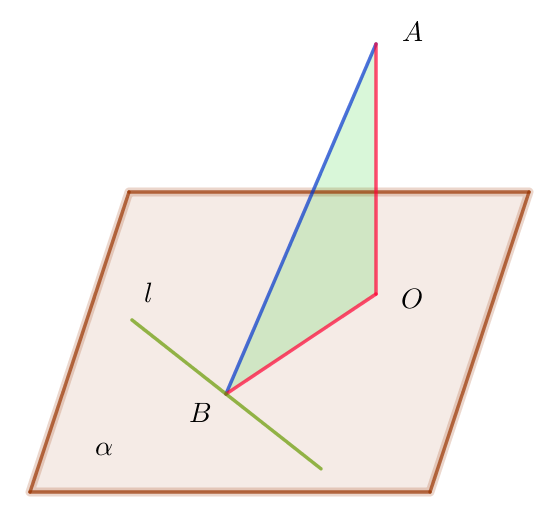
$(2型)$
$平面\alpha 外の点Aより\alpha に下ろした垂線の足をO,Oより$
$平面\alpha 上の直線 \ l \ に下ろした垂線の足をBとすれば、$
$ABと \ l \ は直交する。すなわち$

$\qquad AO \perp \alpha , \ OB \perp l \rightarrow 　AB \perp l$

(証明)
$AO⊥\alpha で、l \ は平面\alpha 上の直線だから、定理3より　AO \perp l$
$仮定より　OB \perp l　だから \ l \ は点Oで交わる2直線AO,OBに$
$垂直となり、定理2より$
$\qquad l \perp 平面ABO $
$よって、ABは平面ABO上の直線だから　AB \perp l$

　
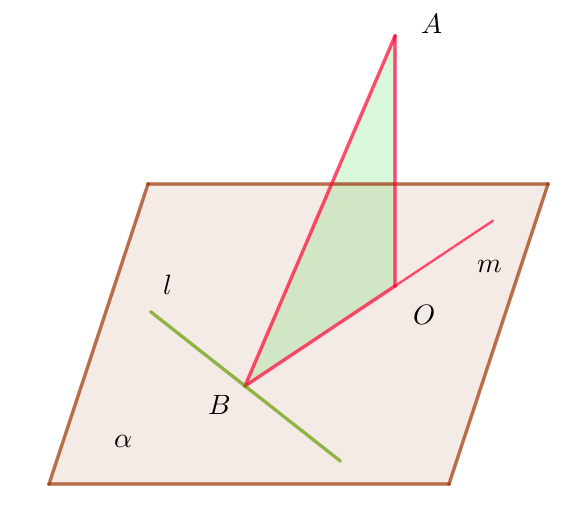
$(3型)$
$平面\alpha 外の点Aより\alpha 上の直線 \ l \ に下ろした垂線の$
$足をB、\alpha 上でBを通り、l \ に垂直な直線を m 、Aより$
$m に下ろした垂線の足をOとすれば、AOと平面\alpha は$
$直交する。すなわち$

$\qquad AB \perp l, \ OB \perp l,\ AO⊥OB \rightarrow \ AO \perp \alpha $

$(証明)$
$AB⊥l、OB \perp l より\ \ l \ は点Bで交わる2直線に垂直だから、l \perp (平面ABO)$
$よって　l \perp AO$
$仮定より　AO \perp OB$
$よって　AOは点Bで交わる、2直線 \ l,m に垂直となり　定理2より \ \ AO \perp \alpha $


$なお、3型は平面\alpha 外の点Aから\alpha に垂線AOを下ろす方法を示しています。$

ページの先頭へ↑