ケプラーの法則から万有引力の法則を導く方法
1 はじめに
$16世紀中頃、ティコ・ブラーエ(デンマーク)は20年以上にわたる肉眼で観測した高精度の$
$膨大な天体観測記録を残した。$
$弟子でもあり共同研究者でもあったヨハネス・ケプラー(ドイツ)はこのデータ整理に没頭し、$
$後に「ケプラーの3大法則」とよばれる大発見をした。$
$\qquad ケプラーの3大法則$
$\quad 法則Ⅰ\ (1609) 惑星は太陽を一つの焦点とする楕円軌道をえがく。$
$\quad 法則Ⅱ\ (1609) 惑星の太陽のまわりの面積速度はそれぞれの惑星ごとに一定である。$
$\quad 法則Ⅲ\ (1619) 公転周期の2乗は、楕円軌道の長半径の3乗に比例する。$
$この頃、ガリレオ・ガリレイが地動説を唱えて宗教裁判にかけられるなど教会が絶対的な権力を$
$持っていた時代の天動説に、地動説の確たる証拠を見つけたわけである。$
$その後、ニュートンはガリレオの自然落下運動の実験結果やケプラーの法則を使って、地球と$
$月の間に働く力の正体を考察し、これがすべての物体間に働く万有引力であるとした。$
$ここでは、ケプラーの3つの法則から万有引力の法則を、微積分を使って導いてみましょう。$
2 法則Ⅱの利用
$平面上で運動している質点Pの位置を極座標(r,\varphi)で表すと加速度は$
$\quad a_r=\cfrac{d^2r}{dt^2} -r\big(\cfrac{d\varphi}{dt}\big)^2 \hspace{16em}(1)$
$\quad a_\varphi=2\cfrac{dr}{dt}\cfrac{d\varphi}{dt}+r \cfrac{d^2\varphi}{dt^2}=\cfrac{1}{r}\cfrac{d}{dt}\big(r^2\cfrac{d\varphi}{dt}\big) \hspace{8em}(2)$
$と表される。($速度・加速度の2次元極座標表示$を参考にしてください)$
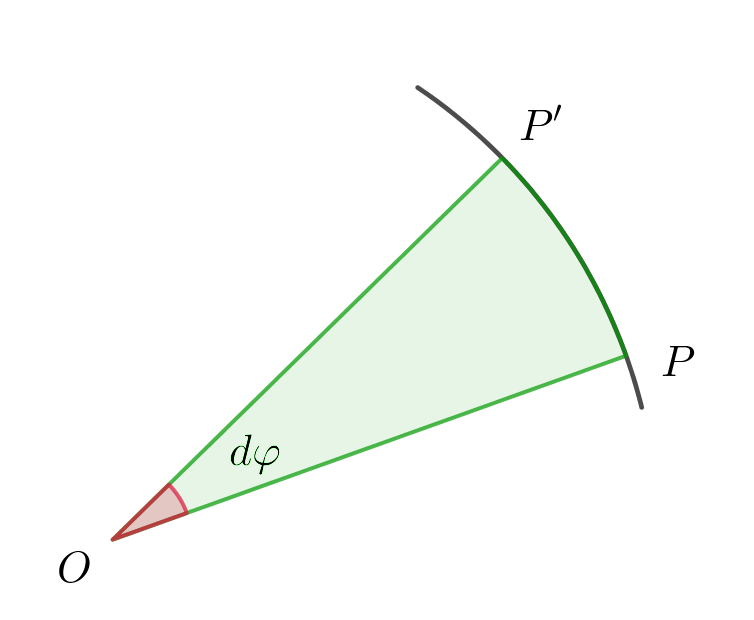
$できる図形は r=OP \fallingdotseq OP' だから扇形としてよい。$
$するとその面積は \cfrac{1}{2}r^2 d\varphi となり、単位時間当たりでは$
$\qquad \cfrac{1}{2}r^2 \cfrac{d\varphi}{dt}$
$となります。これが面積速度といわれるものです。$
$法則Ⅱは、これが惑星ごとに一定であるといっているから$
$\quad \cfrac{1}{2}r^2 \cfrac{d\varphi}{dt}=\cfrac{1}{2}k \quad (kは定数)とおくと$
$\quad r^2 \cfrac{d\varphi}{dt}=k \hspace{20em}(3)$
$なお、mは惑星の質量として、mr^2 \cfrac{d\varphi}{dt} \ \ を今は角運動量といいますので、この法則Ⅱは$
$「角運動量保存の法則」と呼ばれています。$
$これを(2)に代入すると$
$\qquad a_\varphi=\cfrac{1}{r}\cfrac{d}{dt}k=0$
$となり、これは\varphi 方向には力が働かないことを示しています。$
$すると惑星に働く力はr方向のみとなるから$
$\quad F=ma_r=m\big(\cfrac{d^2r}{dt^2} -r(\cfrac{d\varphi}{dt})^2\big) \hspace{10em}(4)$
2 法則Ⅰの利用
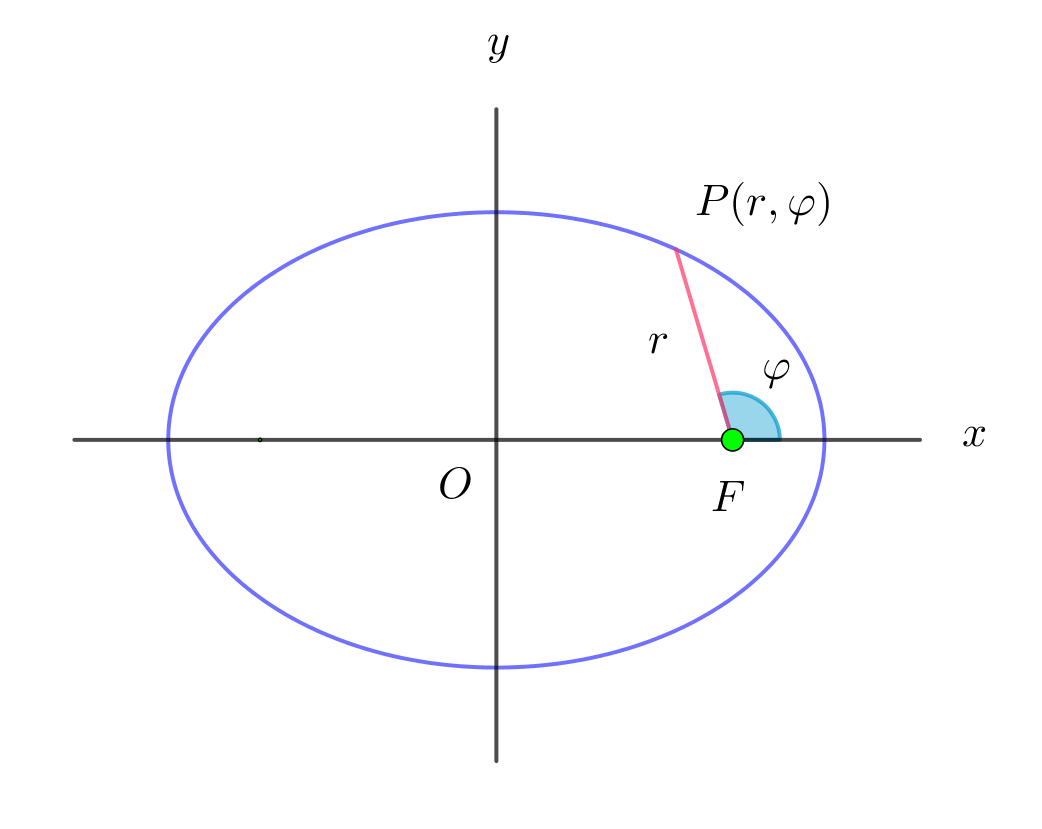
$離心率をeとすると 0 < e <1 \ で r=\cfrac{l}{1+e\cos \varphi} \ とおける。$
$ただし、\varphi=\cfrac{\pi}{2} \ のとき r=l \ である。$
$この表現については($ 楕円$を参考にしてください)$
$これより \cfrac{l}{r}=1+e\cos \varphi \hspace{13em}(5)$
$l とe は定数であることに注意して、tで微分すると$
$\quad -\cfrac{l}{r^2}\cfrac{dr}{dt}=-e\sin \varphi \cfrac{d\varphi}{dt}$
$\quad \cfrac{dr}{dt}=\cfrac{e}{l}\sin \varphi \times r^2\cfrac{d\varphi}{dt}$
$(3)を代入して \cfrac{dr}{dt}=\cfrac{ke}{l}\sin \varphi $
$さらにtで微分して$
$\quad \cfrac{d^2r}{dt^2}=\cfrac{ke}{l}\cos \varphi \times \cfrac{d\varphi}{dt}$
$もう一度(3)をつかって$
$\quad \cfrac{d^2r}{dt^2}=\cfrac{ke}{l}\cos \varphi \times \cfrac{k}{r^2}=\cfrac{k^2}{lr^2}\ e\cos \varphi $
$(5)より e\cos \varphi =\cfrac{l}{r}-1 \ \ を代入して$
$\quad \cfrac{d^2r}{dt^2}=\cfrac{k^2}{lr^2}(\cfrac{l}{r}-1)=\cfrac{k^2}{r^3}-\cfrac{k^2}{lr^2}$
$(3)より \cfrac{d\varphi}{dt}=\cfrac{k}{r^2} \ \ だから(4)は$
\begin{eqnarray*} F&=&m\big(\cfrac{d^2r}{dt^2} -r(\cfrac{d\varphi}{dt})^2\big)\\ &=&m\big(\cfrac{k^2}{r^3}-\cfrac{k^2}{lr^2}-r(\cfrac{k}{r^2})^2\big)\\ &=&-\cfrac{mk^2}{l}\cfrac{1}{r^2} \hspace{17em}(6) \end{eqnarray*} $となって、力Fが距離rの逆2乗に比例することがわかりました。$
3 法則Ⅲの利用
$惑星の周期をTとすると 楕円 \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 の面積は\pi ab だから($ 楕円$を参考にしてください)$
$\quad \cfrac{\pi ab}{T} は面積速度となります。$
$したがって \cfrac{1}{2}r^2 \cfrac{d\varphi}{dt}=\cfrac{1}{2}k=\cfrac{\pi ab}{T} より k=\cfrac{2\pi ab}{T}$
$また、楕円の性質より l=\cfrac{b^2}{a} \qquad ($ 楕円$を参考にしてください)$
$これらを(6)に代入して$
\begin{eqnarray*} F&=&-m \times \cfrac{a}{b^2}\times \big(\cfrac{2\pi ab}{T}\big)^2 \times \cfrac{1}{r^2}\\ &=&-\cfrac{4\pi ^2 a^3}{T^2} \times \cfrac{m}{r^2} \hspace{13em}(7)\\ \end{eqnarray*} $ここで法則Ⅲを使います。$
$どの惑星も公転周期の2乗と楕円軌道の長半径の3乗は比例しますから、比例定数を\lambda とおく。$
$ただし、\lambda は全惑星に共通な定数です。$
$\quad \cfrac{a^3}{T^2}=\lambda $
$すると(7)は$
$\quad F=-4\pi ^2 \lambda \ \cfrac{m}{r^2} $
$となります。ここで、ニュートンは、この力Fは太陽が惑星を引く力であるが、運動法則Ⅲ$
$「作用・反作用の法則」 により、惑星が太陽を引く力でもあると考えました。$
$したがって、Fは太陽の質量Mにも比例することになりますから$
$\quad F=-G\cfrac{Mm}{r^2} \quad (Gは万有引力定数とよばれています)$
$これで、万有引力の法則が導けました。$
$なお、ニュートンは大著「プリンキピア」で微分法とその逆演算である積分法を発見し,$
$発表しているにもかかわらず、万有引力の法則のみならず、ほとんどすべての命題を$
$従来の幾何を使って説明しています。$
メインメニュー に戻る