速度・加速度の2次元極座標表示

　

$右図のように、x\ 軸、y\ 軸上の基本ベクトルを \ \vec{i},\ \vec{j}\ とし、$

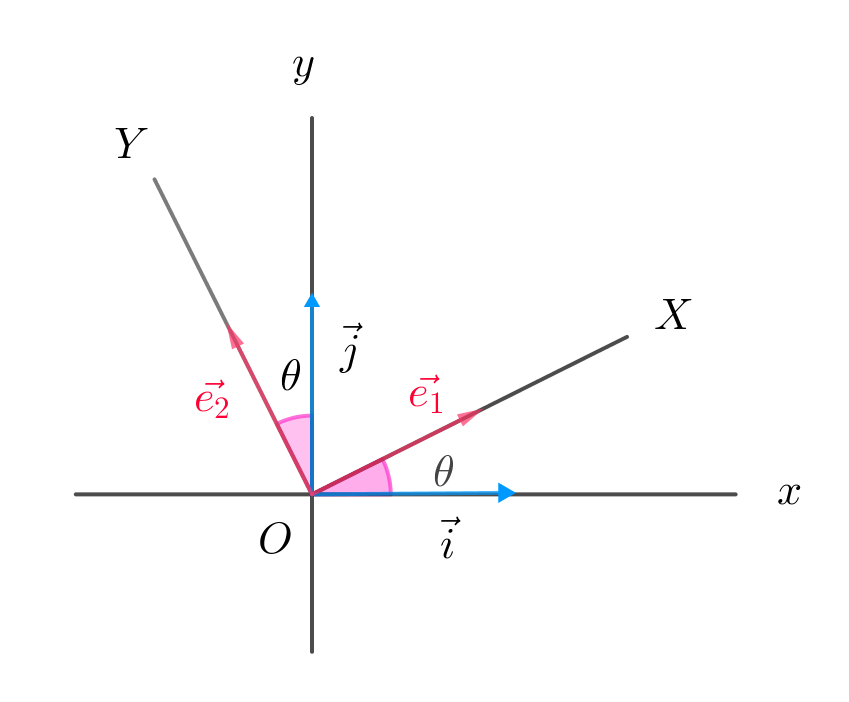
$原点の回りに角 \ \theta \ 回転させた軸を \ X\ 軸,\ Y\ 軸とし、$

$それらの単位ベクトルをそれぞれ \ \vec{e_1}_,\ \vec{e_2}\ とする。$


$座標平面上の点 \ P\ について、OP=r,\ 線分\ OP\ とx\ 軸のなす角を$

$\theta \ とする。$

$\vec{OP}\ の方向を\ r\ 軸方向といい、上の説明の \ X\ 軸に相当する。$

$Y\ 軸に相当する軸を\ \theta \ 軸という。$

　

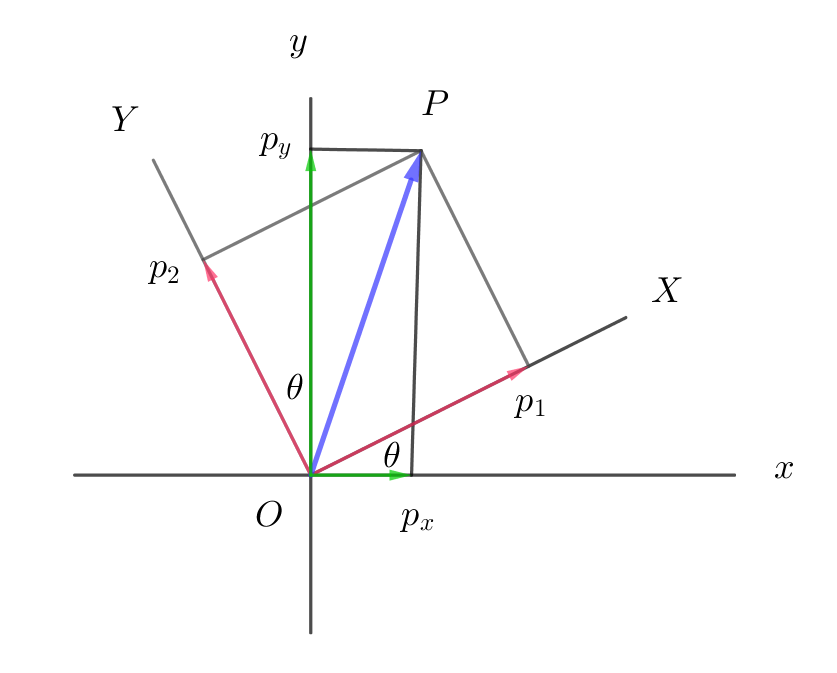
$\vec{OP}=\vec{p}\ をx,\ y\ 座標軸で表したときの成分を \ (p_x,\ p_y)\ とすると$

$x,\ y\ 直交座標と極座標には$

$\qquad x=r\cos \theta , \quad y=r\sin \theta $

$の関係がある。$

$\vec{p}\ を\ X,\ Y\ 座標軸で表したときの成分を \ (p_1,\ p_2)\ とすると$

$\qquad p_1=p_x\ \cos \theta + p_y\ \sin \theta$
$\qquad p_2=-p_x\ \sin \theta +p_y\ \cos \theta $

$逆に、\vec{p}\ を\ x,\ y\ 座標軸で表したときの成分を \ (p_x,\ p_y)\ とすると$
\begin{eqnarray*} \vec{p}&=&p_1\ \vec{e_1}+p_2\ \vec{e_2}\\ &=&p_1(\cos \theta \ \vec{i}+\sin \theta \ \vec{j})+p_2(-\sin \theta \ \vec{i}+\cos \theta \ \vec{j})\\ &=&(p_1\cos \theta - p_2\sin \theta)\ \vec{i}+(p_1\sin \theta +p_2\cos \theta)\ \vec{j}\\ \end{eqnarray*}
$\qquad p_x=p_1\ \cos \theta - p_2\ \sin \theta$
$\qquad p_y=p_1\ \sin \theta + p_2\ \cos \theta $

$このことについては($回転の表す単位ベクトル$)を参考にしてください。$


$(1)　速度の極座標表示$

$点Pが時間とともに運動するとき、速度の\ x,\ y,\ r,\ \theta \ 成分をそれぞれ\ v_x,\ v_y,\ v_r,\ v_\theta \ とすると$

$\qquad v_x=\cfrac{dx}{dt}=\cfrac{d}{dt}(r\cos \theta)=\cfrac{dr}{dt}\cos \theta -r\sin \theta \cfrac{d\theta}{dt}$

$\qquad v_y=\cfrac{dy}{dt}=\cfrac{d}{dt}(r\sin \theta)=\cfrac{dr}{dt}\sin \theta +r\cos \theta \cfrac{d\theta}{dt}$

$\vec{v}=(v_x,\ v_y) \ を\ (v_r,\ v_\theta) \ で表すには上のp_1,\ p_2の式を利用して$

\begin{eqnarray*} v_r &=&v_x\cos \theta + v_y\sin \theta\\ \\ &=&\big(\cfrac{dr}{dt}\cos \theta -r\sin \theta \cfrac{d\theta}{dt}\big)\cos \theta +\big(\cfrac{dr}{dt}\sin \theta +r\cos \theta \cfrac{d\theta}{dt}\big)\sin \theta\\ \\ &=&\cfrac{dr}{dt}\cos ^2 \theta + \cfrac{dr}{dt}\sin ^2 \theta \\ \\ &=&\cfrac{dr}{dt}\\ \end{eqnarray*}
\begin{eqnarray*} v_\theta &=&-v_x\sin \theta + v_y\cos \theta\\ \\ &=&-\big(\cfrac{dr}{dt}\cos \theta -r\sin \theta \cfrac{d\theta}{dt}\big)\sin \theta +\big(\cfrac{dr}{dt}\sin \theta +r\cos \theta \cfrac{d\theta}{dt}\big)\cos \theta\\ \\ &=&r\sin ^2\theta \cfrac{d\theta }{dt} + r\cos ^2\theta \cfrac{d\theta }{dt} \\ \\ &=&r \cfrac{d\theta }{dt}\\ \end{eqnarray*}

$(2)　加速度の極座標表示$

$加速度の\ x,\ y,\ r,\ \theta \ 成分をそれぞれ \ a_x,\ a_y,\ a_r,\ a_\theta \ とすると$

\begin{eqnarray*} a_x &=&\cfrac{dv_x}{dt}\\ \\ &=&\cfrac{d}{dt}\big(\cfrac{dr}{dt}\cos \theta -r\sin \theta \cfrac{d\theta}{dt}\big)\\ \\ &=&\cfrac{d^2r}{dt^2}\cos \theta +\cfrac{dr}{dt}(-\sin \theta)\cfrac{d\theta}{dt}-\cfrac{dr}{dt}\sin \theta \cfrac{d\theta}{dt} -r\big\{\cos \theta \big(\cfrac{d\theta}{dt}\big)^2+\sin \theta \cfrac{d^2\theta}{dt^2}\big\}\\ \\ &=&\cfrac{d^2r}{dt^2}\cos \theta -2\sin \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\cos \theta \big(\cfrac{d\theta}{dt}\big)^2-r\sin \theta \cfrac{d^2\theta}{dt^2}\\ \end{eqnarray*}
\begin{eqnarray*} a_y &=&\cfrac{dv_y}{dt}\\ \\ &=&\cfrac{d}{dt}\big(\cfrac{dr}{dt}\sin \theta +r\cos \theta \cfrac{d\theta}{dt}\big)\\ \\ &=&\cfrac{d^2r}{dt^2}\sin \theta +\cfrac{dr}{dt}\cos \theta\cfrac{d\theta}{dt}+\cfrac{dr}{dt}\cos \theta \cfrac{d\theta}{dt} +r\big\{-\sin \theta \big(\cfrac{d\theta}{dt}\big)^2+\cos \theta \cfrac{d^2\theta}{dt^2}\big\}\\ \\ &=&\cfrac{d^2r}{dt^2}\sin \theta +2\cos \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\sin \theta \big(\cfrac{d\theta}{dt}\big)^2+r\cos \theta \cfrac{d^2\theta}{dt^2}\\ \end{eqnarray*}
$\vec{a}=(a_x,\ a_y) \ を\ (a_r,\ a_\theta) \ で表すには上の \ p_1,\ p_2\ の式を利用して$

\begin{eqnarray*} a_r &=&a_x\cos \theta + a_y\sin \theta\\ \\ &=&\big(\cfrac{d^2r}{dt^2}\cos \theta -2\sin \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\cos \theta \big(\cfrac{d\theta}{dt}\big)^2-r\sin \theta \cfrac{d^2\theta}{dt^2}\big)\cos \theta \\ && \qquad +\big(\cfrac{d^2r}{dt^2}\sin \theta +2\cos \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\sin \theta \big(\cfrac{d\theta}{dt}\big)^2+r\cos \theta \cfrac{d^2\theta}{dt^2}\big)\sin \theta \\ \\ &=&\cfrac{d^2r}{dt^2} -r\big(\cfrac{d\theta}{dt}\big)^2 \\ \end{eqnarray*}

\begin{eqnarray*} a_\theta &=&-a_x\sin \theta + a_y\cos \theta\\ \\ &=&-\big(\cfrac{d^2r}{dt^2}\cos \theta -2\sin \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\cos \theta \big(\cfrac{d\theta}{dt}\big)^2-r\sin \theta \cfrac{d^2\theta}{dt^2}\big)\sin \theta \\ &&\qquad +\big(\cfrac{d^2r}{dt^2}\sin \theta +2\cos \theta \cfrac{dr}{dt}\cfrac{d\theta}{dt}-r\sin \theta \big(\cfrac{d\theta}{dt}\big)^2+r\cos \theta \cfrac{d^2\theta}{dt^2}\big)\cos \theta \\ \\ &=&2\cfrac{dr}{dt}\cfrac{d\theta}{dt}+r \cfrac{d^2\theta}{dt^2} \\ \\ &=&\cfrac{1}{r}\cfrac{d}{dt}\big(r^2\cfrac{d\theta}{dt}\big)\\ \end{eqnarray*}

ページの先頭へ↑



メインメニュー　に戻る