質量中心（重心）


(1)　定義


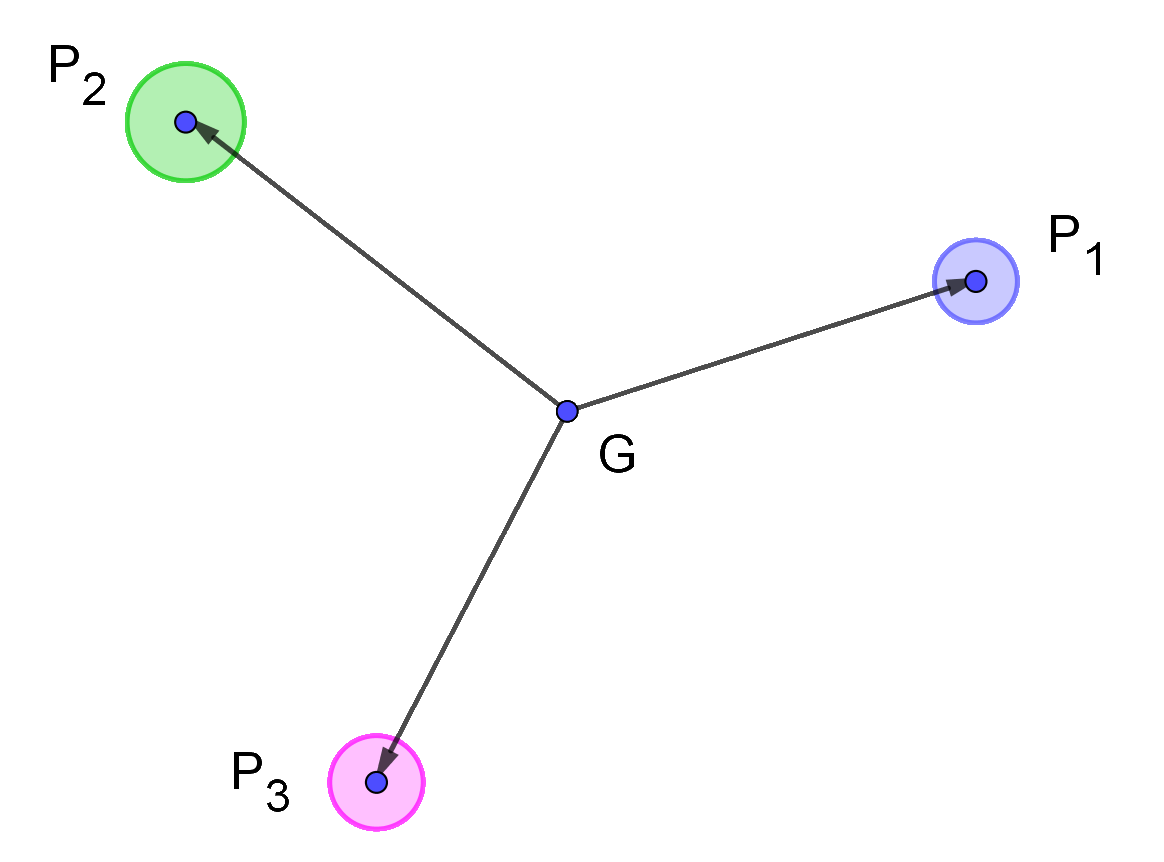
$空間に質量m_iの質点Piがあるとき$
\[\sum_i m_i\vec{GPi}=\vec{0}\hspace{16em}\] $となる点Gを質量中心（重心）といいます。$
$これを変形すると$
\[\sum_i m_i(\vec{OP_i}- \vec{OG})=\vec{0} \hspace{15em}\] \[\sum_i m_i\vec{OP_i}= \sum_i m_i \vec{OG} \hspace{33em}\] \[\vec{OG}=\cfrac{\sum m_i\vec{OP_i}}{\sum m_i}\hspace{36em}\]


(2)　２質点の重心


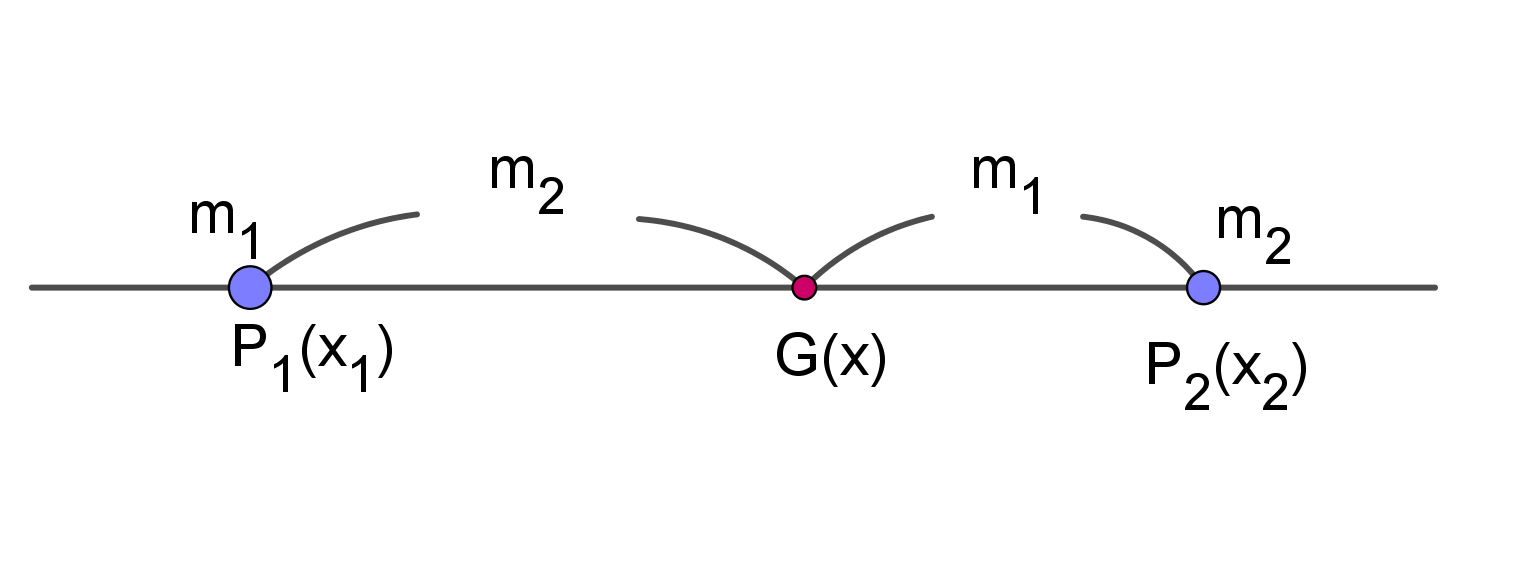
$x軸上に、質量m_1の質点P_1(x_1),質量m_2の質点P_2(x_2)$
$がある系の重心G(x)は定義より$
$\hspace{2em} \vec{OG}=\cfrac{m_1\vec{OP_1}+m_2\vec{OP_2}}{m_1+m_2}$
$\hspace{2em} \therefore x=\cfrac{m_1x_1+m_2x_2}{m_1+m_2}$

$したがって、G \ は線分 \ P_1 P_2 \ を \ m_2 \ : \ m_1 \ の比に内分する点になります。$


(3)　平面上の連続体の重心

$面密度が \rho (一定)の図形Fの重心G(G_x,G_y)は$
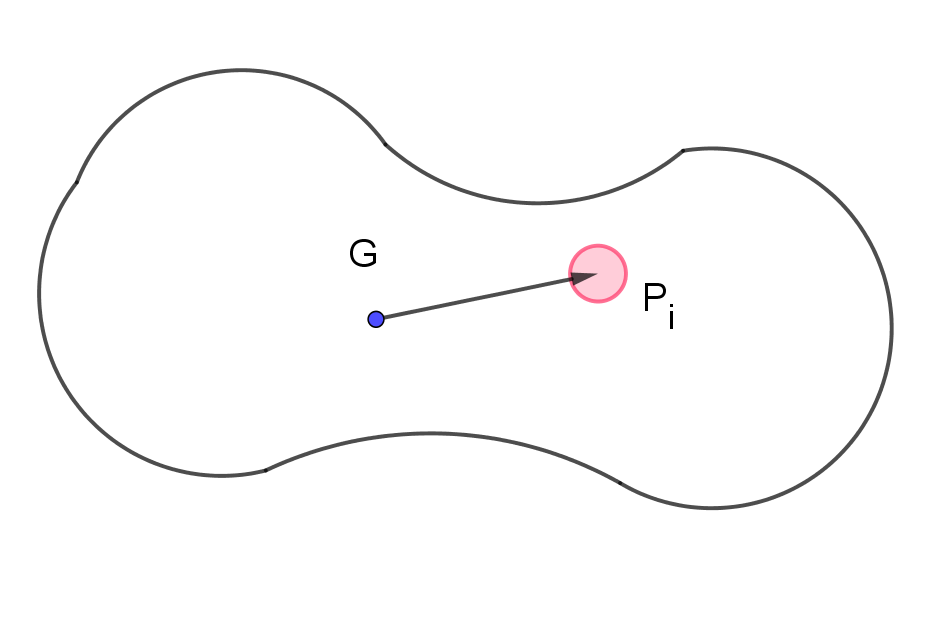
$位置P_iの微小面積をdS_i, \ 微小質量をdm_i とすると$
$\hspace{2em} dm_i=\rho dS_i \quad だから$

$\hspace{2em} \vec{OG}=\cfrac{\sum dm_i\vec{OP_i}}{\sum dm_i}$

$\hspace{2em} G_x=\cfrac{\int\rho dS \ x}{\int \rho dS}= \cfrac{\int xdS}{\int dS}$

同様にして

$\hspace{2em} G_y=\cfrac{\int\rho dS \ y}{\int \rho dS}= \cfrac{\int ydS}{\int dS}$

$とくに、図形Fをx軸に垂直な直線で切ったときの切り口の長さをf(x)とすると$

$\hspace{2em} dS=f(x)dx 　だから$

$\hspace{2em} G_x=\cfrac{\int _a^b xf(x)dx}{\int _a^b f(x)dx}$


$以上のことを押さえた上で、次の問題を考えて見ましょう。$


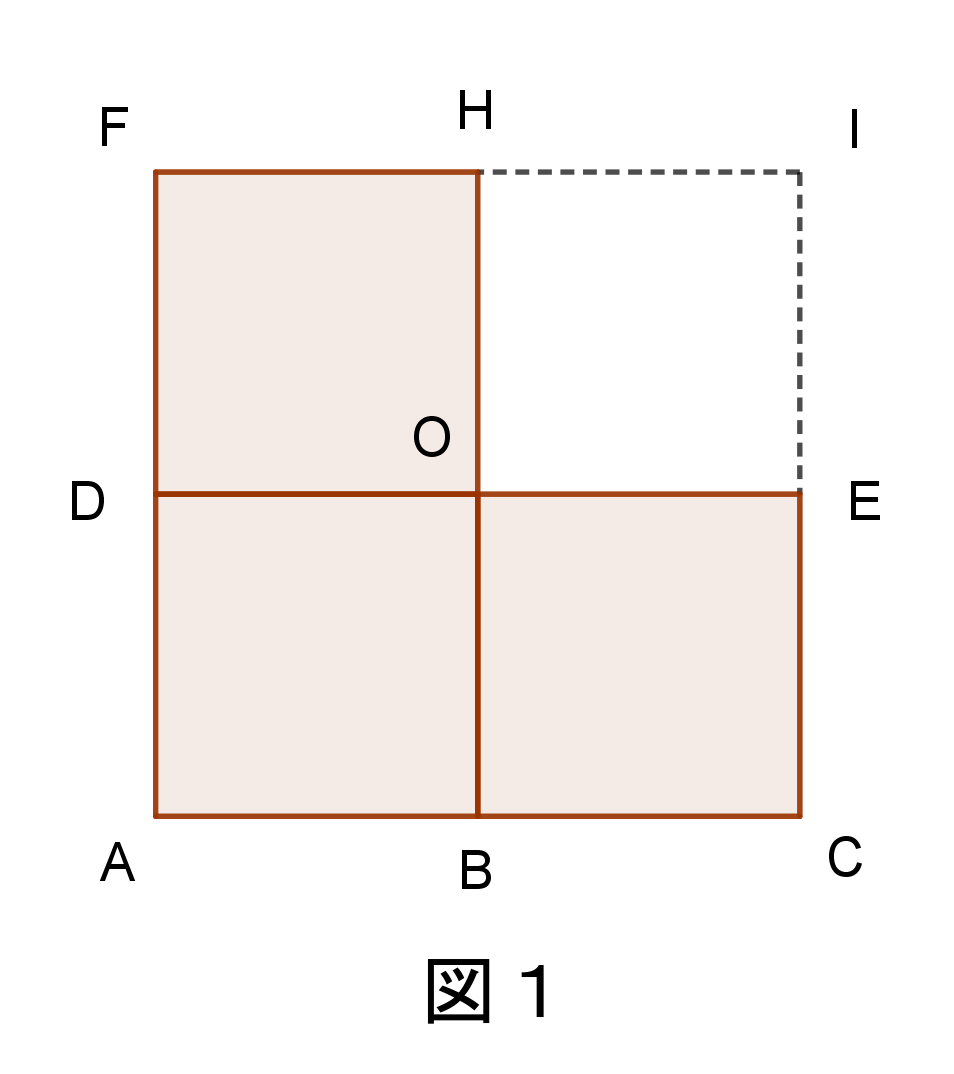
問題１

$図1のように、1辺2aの正方形から1辺aの正方形を切り取った図形の$
$重心を求めましょう。$


$解答１（積分法）$


$点Aを原点とし、直線ACをx軸、直線AFをy軸と考える。$
$重心Gのx座標をG_xとすると$

$\hspace{2em} G_x=\cfrac{\int_0^a x2\rho dx+ \int _a^{2a}x \rho dx}{\int _0^a2\rho dx + \int _a^{2a}\rho dx}$

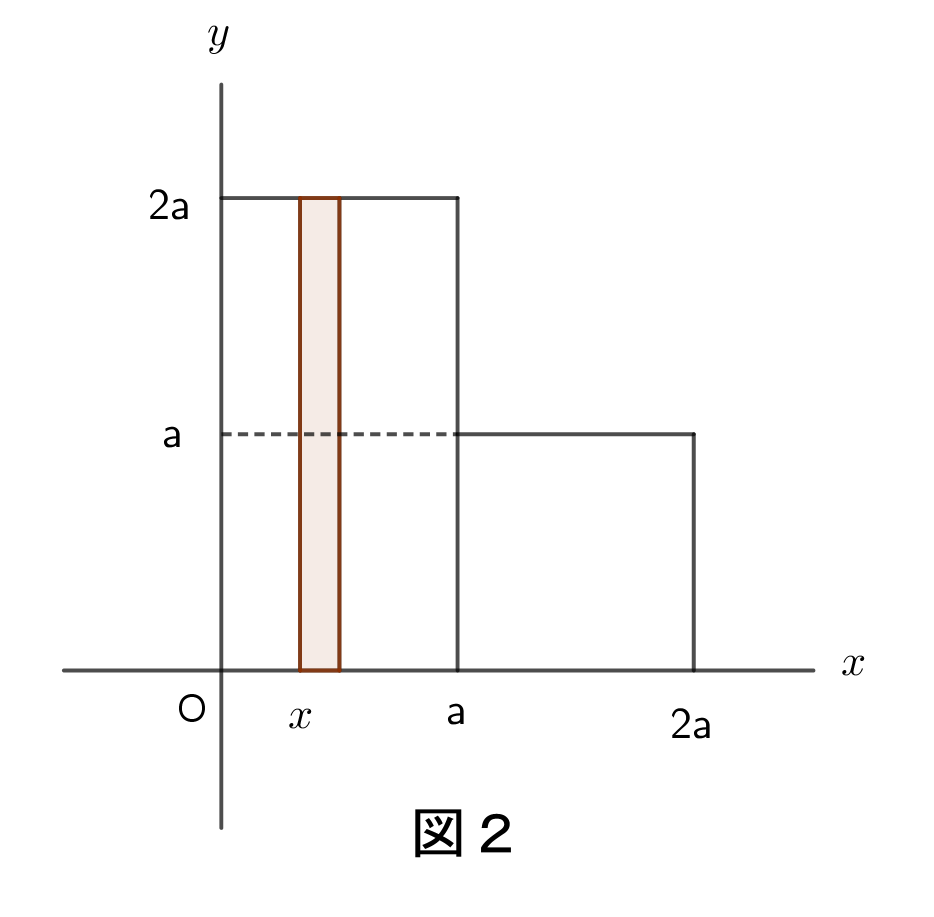
$\hspace{4em} =\cfrac{[x^2]_0^a+[\cfrac{x^2}{2}]_a^{2a}}{2a+a}$
$\hspace{4em} =\cfrac{5}{6}a$

$図形の対称性から、重心は対角線OA上にあるから$
$\hspace{2em} AG=\sqrt{2}AG_x=\sqrt{2} \times \cfrac{5}{6}a$
$したがって$
$\hspace{2em} OG=\sqrt{2}a-AG=\cfrac{\sqrt{2}}{6}a$

$解答２（２質点の重心）$

$直線ACをx軸、点Aを原点とした数直線で考える。$
長方形$ABHFの質量は2,重心のx座標G_1はABの中点だから　 G_1(\cfrac{a}{2})$
正方形$BCEOの質量は1,重心のx座標G_2はBCの中点だから　 G_2(\cfrac{3}{2}a)$

求める重心の$x座標G_xは線分G_1G_2を1:2$に内分する点だから
$\hspace{2em} G_x=\cfrac{2 \times \cfrac{a}{2}+ 1 \times \cfrac{3a}{2}}{1+2}=\cfrac{5}{6}a$


解答３（切り取った正方形の重心を考慮する方法）

切り取った正方形の重心$G_1は　 OG_1=\cfrac{\sqrt{2}}{2}a$
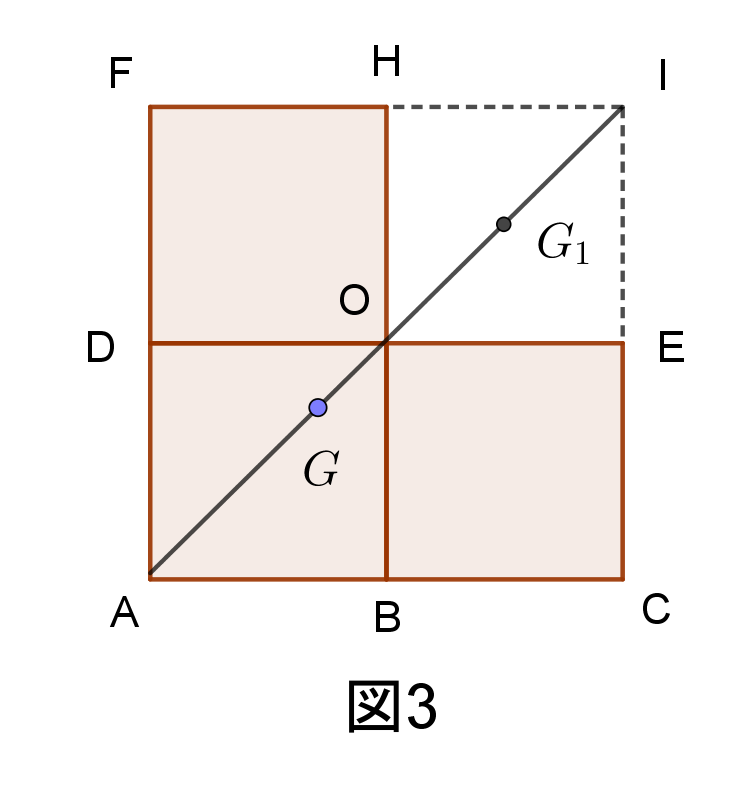
正方形$3つ分の重心をG$とすると、
正方形$4つ分の重心が点O$であるから
点$Oは線分GG_1を \ 1:3 \ $に内分する点である。

$\hspace{2em} OG:OG_1=1:3$

$\hspace{2em} OG=\cfrac{OG_1}{3}= \cfrac{\sqrt{2}}{6}a$

だいぶ昔のことですが、この問題と解答３は、
ある物理の先生から教わったもので、感動したのを覚えています。
数学を勉強してきた者（少なくとも小生）にとっては、思いもつかない方法です。
これが、数学と物理を学ぶ者の発想の違いと言えるかもしれません。
この原稿を書いた理由はここにあります。

このやり方を知って次の問題２を考えてみましょう。

問題２


$図４のように、半径 \ 2r の円Oから、半径 \ r \ の円O'を切り取った図形の重心を求めよ。$

解答
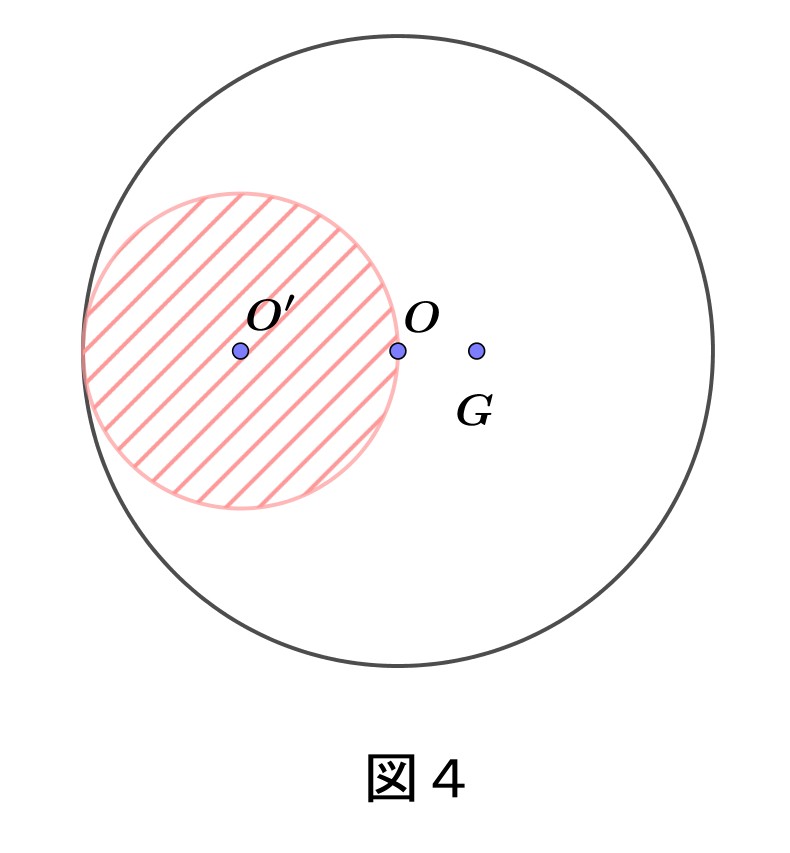
対称性により、重心$Gは直線OO'$上にある。
元の円の面積は$\pi(2r)^2=4\pi r^2$ だから切り取られて残った
図形の面積は$3\pi r^2$
点$OはGO'を3\pi r^2:\pi r^2=1:3$ の比に内分するから
$\hspace{2em} OG:OO'=1:3$
$\hspace{2em} \therefore OG=\cfrac{1}{3}OO'=\cfrac{r}{3}$


(4)　重心とパップス・ギュルダンの定理


$回転体の体積を求める方法に、パップス・ギュルダンの定理$ $(パップス・ギュルダンの定理参照)$ $がありますが、これは回転させる図形の重心がからみますので、回転体の体積が簡単に求まる場合には$
$逆に、重心の位置を求めることができます。$

　　回転体の体積=(重心$G$の移動距離) $\times$ (面積)

$から \hspace{3em} G_x=\cfrac{V}{2\pi S}$

これをつかって次の問題を考えてみましょう。

問題３　半円の重心

面密度$\rho$ が一様な半径$a$の半円を、直径の回りに回転させると
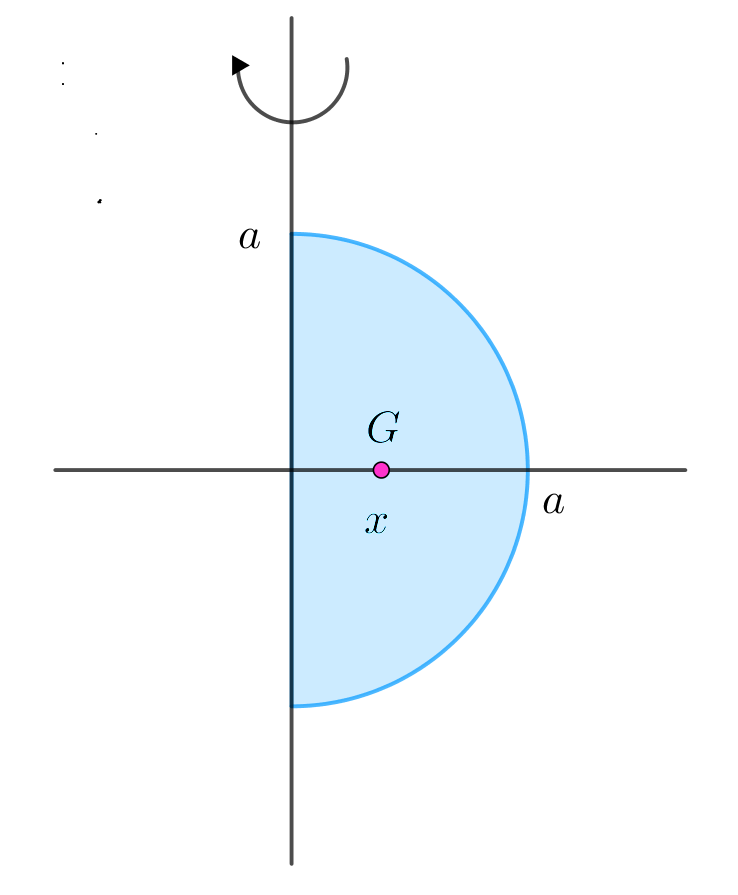
球になる。
$半円の重心の位置を中心からxとすると、パップス・ギュルダンの$
定理から
$\hspace{2em} \cfrac{4}{3}\pi a^3=2\pi x \times \cfrac{1}{2}\pi a^2$
$\hspace{2em} \therefore x=\cfrac{4a}{3\pi}$

別解

これを、重心の定義からまともに計算すると次のようになります。

半円上の任意の点$P(x,y)$を極座標で表すと
$\hspace{2em} 0 \leqq r \leqq a , \quad -\cfrac{\pi}{2} \leqq \theta \leqq \cfrac {\pi}{2}$ として

$\hspace{2em} x=r\cos \theta , \quad dS=rdrd\theta ,\quad dm=\rho dS$ だから

$\hspace{3em} G_x=\cfrac{\int _S r\cos \theta \rho dS}{\int _S \rho dS}$
\[分子 = \int _S r^2\cos \theta dr d\theta = \int _0^a r^2dr \int _{-\cfrac {\pi}{2}}^{\cfrac{\pi}{2}}\cos \theta d\theta =\cfrac{2}{3}a^3 \hspace{25em}\] $\hspace{3em} 分母 =\cfrac{1}{2}\pi a^2$ (半円の面積)より

$\hspace{3em} G_x=\cfrac{\cfrac{2}{3}a^3}{\cfrac{1}{2}\pi a^2}=\cfrac{4a}{3\pi}$




ページの先頭へ↑




メインメニュー　に戻る