パップス・ギュルダンの定理
$パップス・ギュルダンの定理があります。$
$これには回転させる図形の重心がからみますので、$
$回転体の体積が簡単に求まる場合には逆に、重心の$
$位置を求めることができます。$
$平面図形FをFと交わらない直線lの回り$
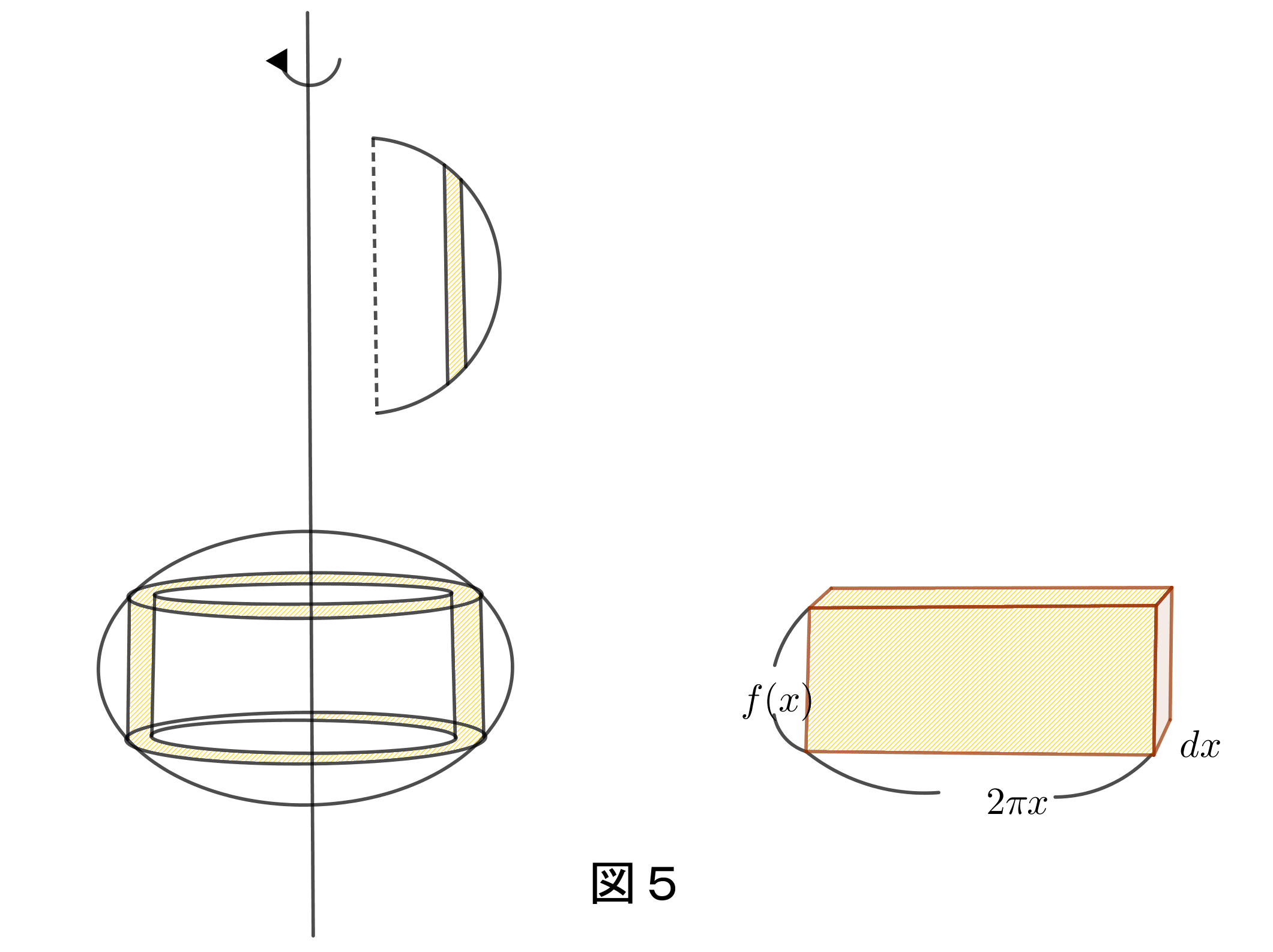
に回転させてできる回転体の体積は図5
のような、バウムクーヘン型積分を使って
$\hspace{2em} \Delta V=2\pi xf(x)\Delta x だから$
\[V=\int _a^b2\pi xf(x)dx=2\pi \int _a^b xf(x)dx=2\pi G_x S \hspace{28em} \] すなわち
回転体の体積=(重心$G$の移動距離) $\times$ (面積)
となります。これが有名なパップス・ギュルダンの定理です。
この式から
$\hspace{3em} G_x=\cfrac{V}{2\pi S}$
となって、重心の位置が求まります。
これをつかって次の問題を考えてみましょう。
問題3 半円の重心
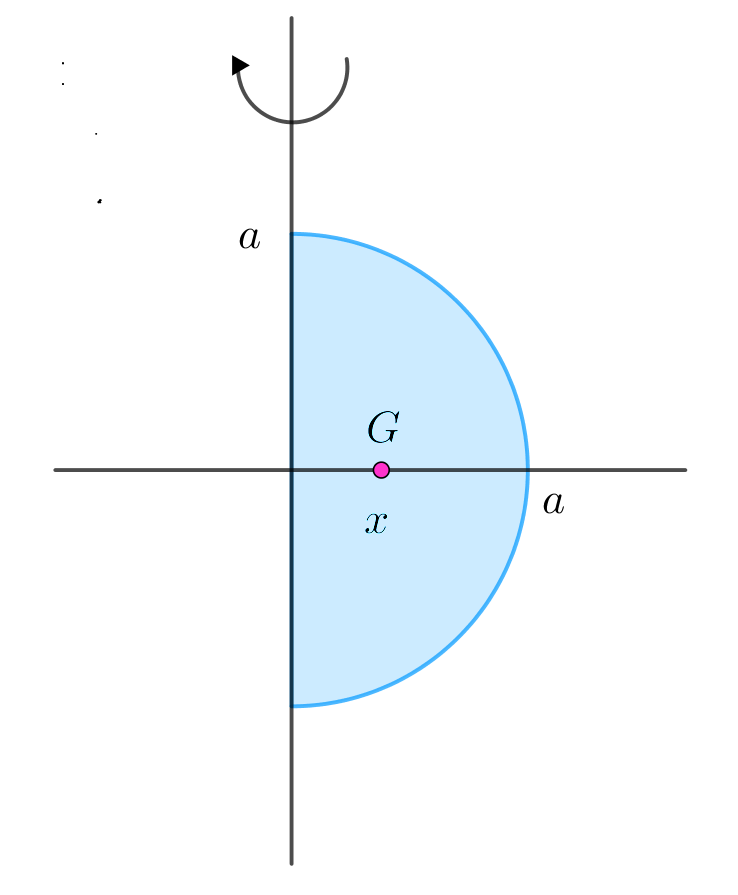
球になる。
$半円の重心の位置を中心からxとすると、パップス・ギュルダンの$
定理から
$\hspace{2em} \cfrac{4}{3}\pi a^3=2\pi x \times \cfrac{1}{2}\pi a^2$
$\hspace{2em} \therefore x=\cfrac{4a}{3\pi}$
メインメニュー に戻る