懸垂線(カテナリー)
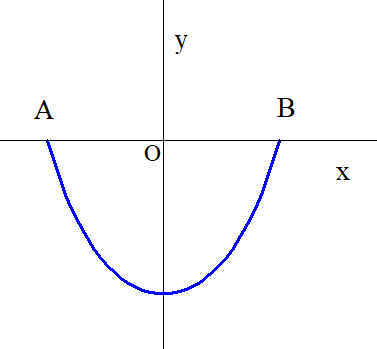
$ひもの両端を水平に持って、吊り下げたときにひもがつくる$
$曲線は?$
$ひもの両端をA(-a,0),B(a,0)とし、任意の点P(x,y)からの$
$微小の長さ(線素といいます)をds,重力加速度をg とすると、$
$質量が m=\rho ds だからこの部分のもつ位置エネルギーdUは$
$\qquad dU=-mgy=-\rho ds g y=-\rho g y \sqrt{1+y'^2}dx$
$したがって$
\[U=-\rho g \int _{-a} ^a y\sqrt{1+y'^2}dx\] $これを最小にする関数 y=y(x) は f(x,y,y')= y \sqrt{1+y'^2} とおくと$
$\qquad \cfrac{\partial f}{\partial x}=0 , \quad \cfrac{\partial f}{\partial y'}=y \cfrac{y'}{\sqrt{1+y'^2}} だから$
$オイラー・ラグランジュの方程式(2)をつかって \ \ ($変分法$を参考にしてください)$
$\qquad \cfrac{d}{dx}\big(f-y'\cfrac{\partial f}{\partial y'}\big) =0 より f-y'\cfrac{yy'}{\sqrt{1+y'^2}} =c \quad (cは定数) とおけるから$
$\qquad y\sqrt{1+y'^2}-y'\cfrac{yy'}{\sqrt{1+y'^2}} =c $
$分母を払って整理すると$
$\qquad y(1+y'^2)-yy'^2=c\sqrt{1+y'^2}$
$\qquad y=c\sqrt{1+y'^2} \quad (ここまできて\ \ y < 0 \ \ だから \ \ c < 0 \ \ であるとわかります)$
$\qquad y'^2=\cfrac{y^2}{c^2}-1 $
$y\ は減少関数だから \ \ y' < 0 $
$\qquad y'=-\sqrt{\cfrac{y^2}{c^2}-1} $
$あとは、この変数分離形の微分方程式を解くだけです。$
$\qquad \cfrac{dy}{\sqrt{\cfrac{y^2}{c^2}-1}}=-dx$
$\qquad \cfrac{dy}{\sqrt{y^2-c^2}}=\cfrac{dx}{c} \qquad (c < 0 \ \ だから) $
$この積分は、大学1年のレベルですが$
$\qquad \log(y+\sqrt{y^2-c^2})=\cfrac{x}{c}+c' \quad (c' は定数)$
$\qquad y+\sqrt{y^2-c^2}=c'e^{\cfrac{x}{c}} \hspace{5em}(1) \qquad (e^{c'} \rightarrow c' と置きかえて)$
$両辺の逆数をとって$
$\qquad \cfrac{1}{y+\sqrt{y^2-c^2}}=\cfrac{1}{c'}e^{-\cfrac{x}{c}}$
$\qquad y-\sqrt{y^2-c^2}=\cfrac{c^2}{c'}e^{-\cfrac{x}{c}} \hspace{5em}(2)$
$(1)+(2)$
$\qquad 2y=c'e^{\cfrac{x}{c}}+\cfrac{c^2}{c'}e^{-\cfrac{x}{c}} \qquad \cfrac{c'}{2} \rightarrow A,\quad \cfrac{c^2}{2c'} \rightarrow B,\quad \cfrac{1}{c} \rightarrow c とおくと$
$\qquad y=Ae^{cx}+Be^{-cx}$
$初期条件は x=\pm a で y=0 だから$
\[ \left\{ \begin{array}{l} Ae^{ca}+Be^{-ca}=0\\ Ae^{-ca}+Be^{ca}=0\\ \end{array} \right. \] $辺々引いて$
$\qquad (A-B)\big(e^{ca}-e^{-ca}\big)=0$
$\qquad \therefore A=B$
$したがって$
$\qquad y=Ae^{cx}+Ae^{-cx}=\cfrac{A}{2}\cfrac{e^{cx}+e^{-cx}}{2}$
$\cfrac{A}{2} \rightarrow A と置きかえて$
$\qquad y=A\cosh cx $
$これがひもが自然に垂れたときにできる曲線で、懸垂線(カテナリー)とよばれています。$
$なお、定数 \ A,\ c\ はひもの長さ、間隔 \ 2a \ によって決まります。$
変分法 に戻る
メインメニュー に戻る