2点間の最短距離

　

$平面上の2定点A,Bを結ぶ曲線のうち、距離が最小と$
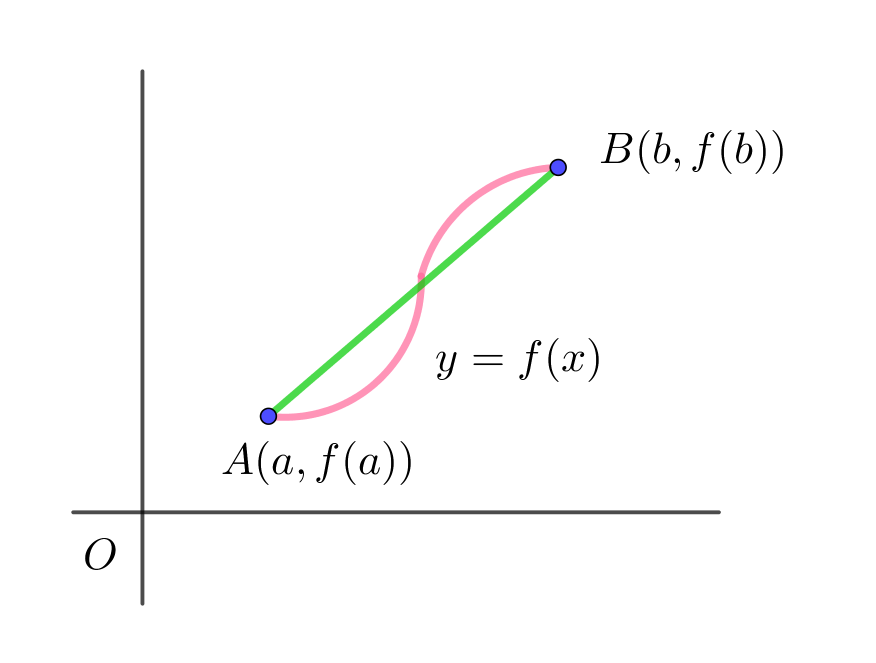
$なる曲線は?$

$2点A,Bを結ぶ曲線を \ y=y(x) \ とすると、曲線の長さは$
\[I=\int _a ^b \sqrt{1+y'^2}dx 　だから\] $\qquad f(x,y,y')= \sqrt{1+y'^2} 　とおくと$

$\qquad \cfrac{\partial f}{\partial y}=0 , \quad \cfrac{\partial f}{\partial y'}=\cfrac{y'}{\sqrt{1+y'^2}} $

$オイラー・ラグランジュの方程式(1)をつかって　($変分法$を参考にしてください)$

$\qquad \cfrac{d}{dx}\cfrac{y'}{\sqrt{1+y'^2}} =0 　より　\cfrac{y'}{\sqrt{1+y'^2}} =c　とおける \quad (cは定数)$

$\qquad y'=c\sqrt{1+y'^2}$

$\qquad y'^2=c^2(1+y'^2)$

$\qquad \therefore y'^2=\cfrac{c^2}{1-c^2}$

$右辺は定数だから あらためて　y'=c 　とおける \quad (c\ は定数)$

$したがって　y=cx+d \quad (d\ は定数) となって、直線であることがわかった。$

$なお、積分定数 \ c,\ d \ は2点A(a,f(a)),B(b,f(b))を通ることから求められる。$





変分法　に戻る


メインメニュー　に戻る