区分求積法と定積分
$区分求積法と定積分の関係について、高校の教科書レベルより少し詳しく、丁寧に解説しました。$
$それでももの足りないなと感じたら、実解析学の本にあたってください。$
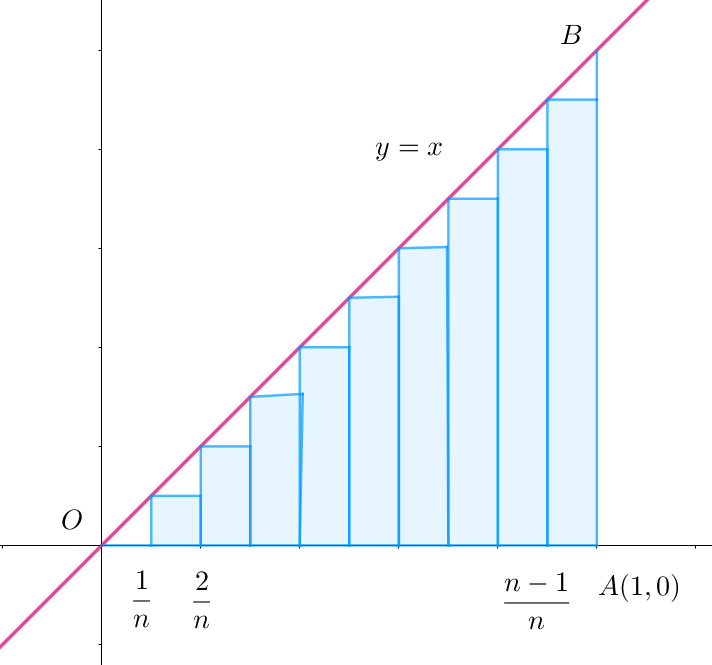
$右図のように、関数 \ f(x)=x\ において、閉区間 \ [0,\ 1]\ を \ n\ 等分し、$
$分点を \ x_0,\ x_1,\ x_2,\ \cdots ,\ x_n\ \ (ただし \ \ x_0=0,\ x_n=1)としたとき、$
$各小区間の長さを \ \Delta x \ で表すと \quad \Delta x=\cfrac{1}{n}$
$このとき、区間 \ [x_k,\ x_{k+1}]\ において、左端の関数値 \ f(x_k)\ を高さ、$
$\Delta x \ を底辺にもつ長方形の面積の和は$
\begin{eqnarray*}
S_n
&=&\cfrac{1}{n}f(\cfrac{0}{n})+\cfrac{1}{n}f(\cfrac{1}{n})+\cdots +\cfrac{1}{n}f(\cfrac{n-1}{n})\\
&=&\cfrac{1}{n}\big(\cfrac{0}{n}\big)+\cfrac{1}{n}\big(\cfrac{1}{n}\big)+\cdots +\cfrac{1}{n}\big(\cfrac{n-1}{n}\big)\\
&=&\cfrac{1}{n^2}(1+2+\cdots +(n-1))\\
&=&\cfrac{1}{n^2}\times \cfrac{(n-1)n}{2}\\
&=&\cfrac{n-1}{2n}\\
\end{eqnarray*}
\[ここで、n \longrightarrow \infty \ \ として分割の幅 \ \Delta \ を限りなく小さくすると \quad \lim _{n \rightarrow \infty}S_n=\cfrac{1}{2}\quad となり\]
$この極限値は \ \triangle OAB \ の面積に一致することがわかります。$
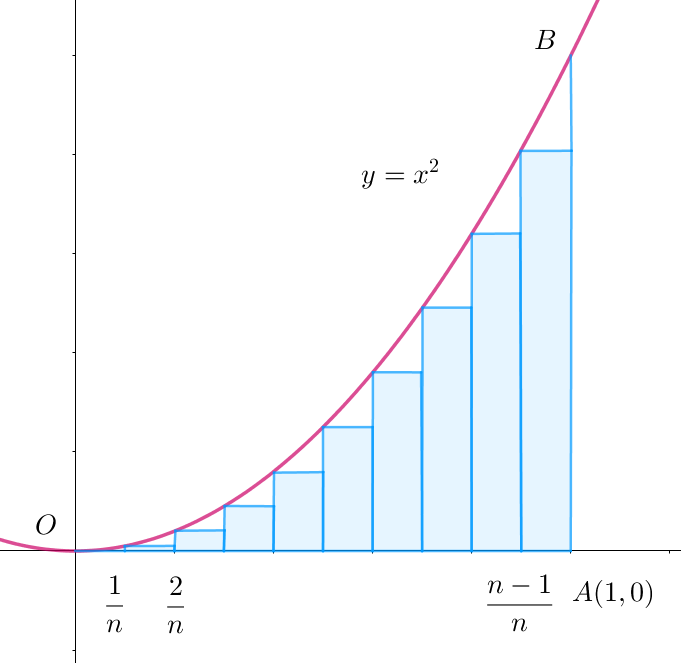
$同じことを関数 \ f(x)=x^2 \ \ について考えてみましょう。$
\begin{eqnarray*}
S_n
&=&\cfrac{1}{n}f(\cfrac{0}{n})+\cfrac{1}{n}f(\cfrac{1}{n})+\cdots +\cfrac{1}{n}f(\cfrac{n-1}{n})\\
&=&\cfrac{1}{n}\big(\cfrac{0}{n}\big)^2+\cfrac{1}{n}\big(\cfrac{1}{n}\big)^2+\cdots +\cfrac{1}{n}\big(\cfrac{n-1}{n}\big)^2\\
&=&\cfrac{1}{n^3}(1^2+2^2+\cdots +(n-1)^2)\\
&=&\cfrac{1}{n^3}\times \cfrac{(n-1)n(2n-1)}{6}\\
&=&\cfrac{(n-1)(2n-1)}{6n^2}\\
\end{eqnarray*}
\[\lim _{n \rightarrow \infty}S_n=\cfrac{1}{3}\]
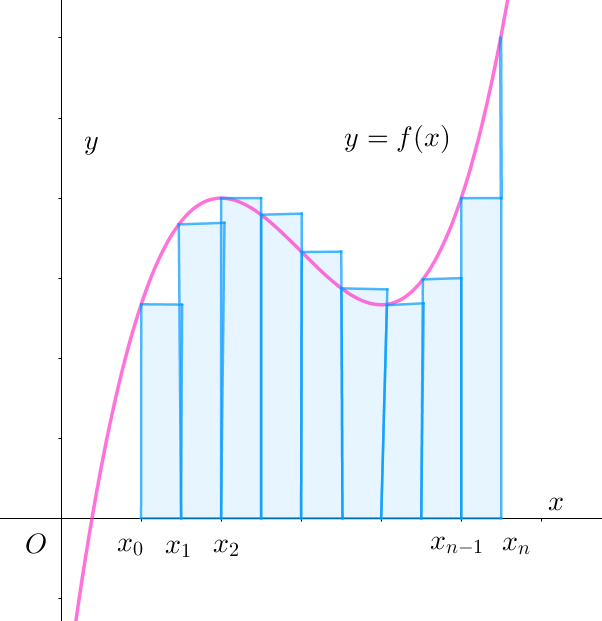
$そこで、一般に次のようなことを考えてみましょう。$
$閉区間 \ [a,\ b]\ で連続な関数 \ f(x)を、この区間で \ n\ 等分し、$
$分点を \ x_0,\ x_1,\ x_2,\ \cdots ,\ x_n\ \ (ただし \ \ x_0=a,\ x_n=b)とする。$
$各小区間の長さを \ \Delta x \ で表すと \quad \Delta x=\cfrac{b-a}{n}$
$このとき、右図のように、区間 \ [x_k,\ x_{k+1}]\ において、左端の$
$関数値 \ f(x_k)\ を高さ、\Delta x \ を底辺にもつ長方形の面積の和$
\[S_n=\sum_{k=0}^{n-1}f(x_k)\Delta x \ \ を考える。\]
$分割の幅 \ \Delta x \ を限りなく細かくしていくとき、すなわち \ \ n \longrightarrow \infty \ \ としたとき$
$この和 \ S_n\ が極限値 \ S\ をもつならば、この \ S\ を \ f(x)\ のa\ から \ b\ までの定積分といい、$
\[\qquad S=\int _a^bf(x)dx\]
$と表す。$
$(注意) \quad この定積分の定義は、この段階では \ f(x)\ の不定積分との関係はまだ何もわかっていません。$
$定積分の定義$
\[\qquad S=\int _a^b f(x)dx=\lim _{n \rightarrow \infty}\sum _{k=0}^{n-1}f(x_k)\Delta x \qquad ただし \ \ \Delta x=\cfrac{b-a}{n} , \quad x_k=a+k\Delta x\]
$f(x)\ が区間 \ [a,\ b]\ で連続で、f(x) \geqq 0 \ \ のときは \ S_n\ は長方形の面積の和を表すから、$
$\qquad \Delta x \longrightarrow \infty \quad のとき \quad S_n \longrightarrow S \quad ならば$
$この極限値 \ S\ は曲線 \ y=f(x)\ と直線 \ x=a,\ x=b\ および \ x\ 軸で囲まれた領域の面積を表すと考えられます。$
$このように、一般的な図形の面積や体積を長方形のような簡単な図形の面積や体積の極限値として求める方法を$
$区分求積法といいます。$
$とくに、a=0,\ \ b=1\ として区間 \ [0,\ 1]\ を \ n\ 等分すると \quad \Delta x=\cfrac{1}{n},\quad x_k=\cfrac{k}{n}\quad だから$
\[\int _0^1 f(x)dx=\lim _{n \longrightarrow \infty} \cfrac{1}{n}\sum _{k=0}^{n-1}f\big(\cfrac{k}{n}\big)\]
$定理1$
\[区間 \ [a,\ b]\ の任意の \ x\ について f(x) \geqq g(x) \quad ならば \quad \int_a^bf(x)dx \geqq \int_a^bg(x)dx\]
$\hspace{5em} ただし、等号はつねに \quad f(x)=g(x)\ \ のとき$
\[とくに、f(x) \geqq 0 \quad ならば \quad \int _a^b f(x)dx >0\]
$\quad 区間 \ [a,\ b]\ の任意の分点で \quad f(x_k) \geqq g(x_k)$
\[したがって \quad f(x_k)\Delta x \geqq g(x_k)\Delta x \quad だから \quad \sum _{k=0}^{n-1}f(x_k)\Delta x \geqq \sum _{k=0}^{n-1}g(x_k)\Delta x \] \[ここで \quad n \longrightarrow \infty \quad とすると \quad \int_a^bf(x)dx \geqq \int_a^bg(x)dx\]
$定理2$
\[\int_a^bf(x)dx =\int_a^cf(x)dx +\int_c^bf(x)dx \quad (a < c < b )\]
$\quad 区間 \ [a,\ b]\ を \ [a,\ c],\ [c,\ b]\ に分割すればよい。$
\[なお、a > b \ \ のとき \ \ \int_a^bf(x)dx =- \int_b^af(x)dx \ \ と定義すると定理 \ 2\ は \ a,\ b,\ c\ の大きさの順によらない。\]
$定理3 \qquad 定積分における平均値の定理$
\[\int_a^bf(x)dx =(b-a)f(c) \quad となる \ c\ が \ a\ と \ b\ の間に少なくとも \ 1\ つ存在する。\]
$\quad a < b \ \ とする。f(x)\ は \ [a,\ b]\ で連続だから最大値 \ M\ と最小値 \ m\ が存在して \quad m \leqq f(x) \leqq M$
$\qquad (これを最大値・最小値定理といいますが、ここでは、証明は略します。)$
\[定理1より \quad \int _a^b mdx \leqq \int _a^b f(x)dx \leqq \int _a^b Mdx\] \[したがって \quad m(b-a) \leqq \int _a^b f(x)dx \leqq M(b-a)\] \[すなわち \quad m \leqq \cfrac{1}{b-a}\int _a^b f(x)dx \leqq M\] \[ここで \quad \cfrac{1}{b-a}\int _a^b f(x)dx=K \ \ (K\ は定数)とおくと \quad m \leqq K \leqq M \] $\qquad 中間値の定理より \quad K=f(c)\ \ となる \ c\ が \ a\ と \ b\ の間に少なくとも \ 1\ つ存在する。$
\[すなわち \quad \int_a^bf(x)dx =(b-a)f(c) \quad となる \ c\ が \ a\ と \ b\ の間に少なくとも \ 1\ つ存在する。\] $\qquad なお、a > b \ \ のときは区間 \ [b,\ a]\ で考えればよい。$
$\hspace{4em}このことについては($定積分における平均値の定理$)も参考にしてください。$
$定理4 \qquad 微分積分学の基本定理$
\[区間 \ [a,\ b]\ 内の任意の \ x\ に対して、\int_a^xf(t)dt =S(x) \quad とおくと \quad S'(x)=f(x)\]
$\qquad すなわち \quad S(x)\ は \ f(x)\ の不定積分の \ 1\ つである。$
\begin{eqnarray*} & &S(x+h)-S(x)\\ \\ &=&\int _a^{x+h} f(t)dt - \int _a^xf(t)dt\\ \\ &=&\int _a^{x+h} f(t)dt + \int _x^af(t)dt \hspace{5em}(定義)\\ \\ &=&\int _x^{x+h} f(t)dt \hspace{11em}(定理2)\\ \\ &=&hf(c) \hspace{14em}(定理3)\\ \end{eqnarray*}
$\quad を満たす \ c\ が \ x\ と \ x+h \ の間に存在するから \quad \cfrac{S(x+h)-S(x)}{h}=f(c)$
$\quad h \longrightarrow 0 \quad とすると \quad 左辺 \ \ \longrightarrow \ \ S'(x),\quad 右辺 \ \ \longrightarrow \ \ f(x) \quad だから \quad S'(x)=f(x)$
$定理5 \qquad 定積分と不定積分の関係 $
\[F(x)\ を \ f(x)\ の不定積分の \ 1\ つとすると \quad \int_a^bf(t)dt =F(b)-F(a))\]
\[定理4より \quad \int _a^bf(t)dt=S(x) \quad も \ f(x)\ の不定積分の \ 1\ つだから \quad S(x)=F(x)+C \ \ (Cは定数)\] \[S(a)=\int _a^af(t)dt=0 \quad だから \quad S(a)=F(a)+C=0 \quad \therefore \ \ C=-F(a)\] $\qquad したがって \quad S(x)=F(x)-F(a)$
\[x=b \ \ とおくと \quad S(b)=\int_a^bf(t)dt=F(b)-F(a)\]
$(補充1)$
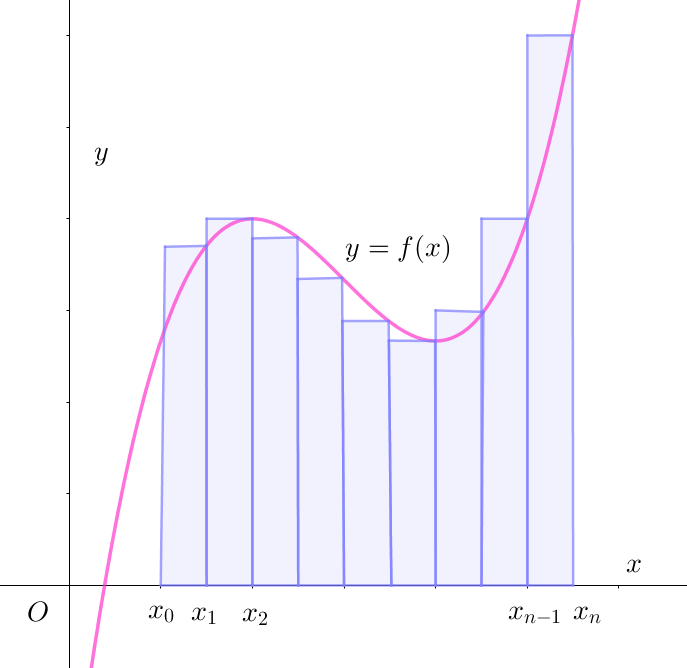
\[定積分の定義で \quad S_n=\sum_{k=0}^{n-1}f(x_k)\Delta x \quad を考えたが\]
\[右図のように \quad T_n=\sum_{k=1}^nf(x_k)\Delta x \quad としても\]
$\qquad \Delta x \ \ \longrightarrow \ \ 0 \quad とすると \ \ S_n \ と \ T_n \ の極限値は一致します。$
$(例1)$
$次のような級数の極限値を考えてみましょう。$
\begin{eqnarray*}
& &\lim _{n \longrightarrow \infty}\Big\{\cfrac{n}{(n+1)^2}+\cfrac{n}{(n+2)^2}+ \cdots +\cfrac{n}{(n+n)^2}\Big\}\\
&=&\lim _{n \longrightarrow \infty}\sum _{k=1}^n \cfrac{n}{(n+k)^2}\\
&=&\lim _{n \longrightarrow \infty}\cfrac{1}{n}\sum _{k=1}^n \cfrac{n^2}{(n+k)^2}\\
&=&\lim _{n \longrightarrow \infty}\cfrac{1}{n}\sum _{k=1}^n \cfrac{1}{(1+\dfrac{k}{n})^2}\\
&=&\int _0^1 \cfrac{dx}{(1+x)^2}\\
&=&\big[-\cfrac{1}{1+x}\big]_0^1\\
&=&\cfrac{1}{2}
\end{eqnarray*}
$(補充2)$
$\quad 区間 \ [a,\ b]\ を必ずしも等分しなくてもよい。[a,\ b]\ を \ n\ 個の小区間に分け、分点を$
$\qquad x_0,\ x_1,\ x_2,\ \cdots , \ x_n \ \ (ただし \ \ x_0=a,\ x_n=b)としたとき$
\[各小区間 \ [x_k,\ x_{k+1}]\ の中にそれぞれ任意に \ 1\ 点 \ c_k\ をとり \quad S_n=\sum _{k=0}^{n-1}f(c_k)\Delta x_k \ \ (\Delta x_k=x_k-x_{k-1})\]
$\quad を考える。n \longrightarrow \infty \ \ のとき \ \ \max \Delta x_k \longrightarrow 0 \ \ となるように細かく分割すると \ \ S_n \ は一定の値に$
$\quad 近づいていくことがわかっています。そこで、この極限値を \ f(x)\ の \ [a,\ b]\ における定積分といいます。$
$\quad 関数 \ f(x)\ が区間 \ [a,\ b]\ で連続でない場合でも、上のような極限値が存在すれば \ f(x)\ は積分可能といいます。$
$\quad 連続な場合は、必ず積分可能となります。$
メインメニュー に戻る